МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

имени В.Н. Каразина

Кафедра физической химии элементы статистической термодинамики

Реферат

студентки 4-го курса

группы Х-141

Миргородской Юлии Валериевны

Харьков 2011

1. Вступление

Рождение статистической термодинамики отмечено точными датами: 1901 г. работа Планка по распределению энергии теплового движения послужила основой квантовой теории, 1902 г. - книга Гиббса, содержавшая основные идеи статистической физики: метод ансамблей. Предшествовали работы Клаузиуса (1857), показавшего, что тепловая энергия - кинетическая энергия движения молекул, Максвелла (1859), сформулировавшего закон распределения молекул газа по скоростям движения и Больцмана в конце XIX века сформулировавшего закон равномерного распределения кинетической энергии по степеням свободы. 1913 г. Бор ввел понятие стационарного квантового состояния: вероятность обнаружить частицу элементе объема на зависит от времени.

Классическая (феноменологическая) термодинамика для расчета термодинамических функций, различных равновесий требует надежно измеренных данных по теплоемкостям веществ, теплотам различных превращений, задания уравнения состояния. Феноменологическая термодинамика дает уравнения связи изменений термодинамических параметров в дифференциальной форме, но для их интегрирования нужно термическое или калорическое уравнения состояния. Вывести эти уравнения феноменологическая термодинамика не может. Феноменологическая термодинамика не дает ответа и на ряд вопросов: почему система стремится к равновесию и остается в равновесии при неизменности макроскопических параметров, как объяснить направленность процессов, что такое температура, энтропия, химический потенциал. Почему C_v 2-х атомного газа равна при низких температурах 3R/2, а при высоких 5R/2?

Для глубокого понимания требуется статистическая физика (правильнее молекулярная статистика) или ее раздел: статистическая термодинамика. Статистическая термодинамика позволяет обосновать и ряд основных формул и законов феноменологической термодинамики. Статистическая термодинамика позволяет связать термодинамические (макро) свойства системы, одинаковые по всему объему равновесной системы, со свойствами составляющих ее частиц, молекул на основе законов движения и взаимодействия микрообъектов, представлениями о вероятности микросостояний. Интуитивно уже в классической термодинамике просматривается такая связь. Второй закон термодинамики дает нам новую функцию - энтропию и мы знаем, что эта функция связана с теплообменом и направлением процесса. Если рассмотреть изменение энтропии от абсолютного нуля, то известно, что при 0K для идеального кристалла она равна 0 и растет с растом температуры. При этом уменьшается степень молекулярной упорядоченности системы. Изменение энтропии при плавления много меньше изменения при испарении. Очевидно, что энтропия связа с упорядоченностью системы, со свойствами молекул, составляющих систему.

2. Основные понятия и элементы статистической термодинамики

Всякая термодинамическая система состоит из очень большого числа механических объектов. Это коллектив из множества однотипных частиц. Частицы в ней могут быть и микроскопическими – атомно-молекулярного размера, и макроскопическими, подобно частицам взвеси в мутной воде или в пыльном воздухе. Для начала неплохо ещё было бы, чтобы они могли каким-то способом перемешиваться.

Если система пребывает в равновесии, то и перемешивание её механических объектов-подсистем в чём-то похоже на стационарное движение, и систему из равновесия не выводит. Оставаясь в нём, тем не менее, она на уровне микрообъектов всё время пребывает в каких-то изменениях, но все они совместимы с одним этим общим равновесием.

Всё множество способов, которыми реализуется макросостояние, для внешнего лабораторного наблюдателя одинаково. Он не может выделить тех различий, которые неизбежны при перемешивании, и ему незаметен постоянный обмен энергией между частицами.

Все эти изменения, которые не выводят систему из равновесия, состоят в непрерывном перераспределении орбитальных конфигураций в огромном фазовом пространстве, которое представляет из себя не что иное, как множество всех орбиталей, порождаемых всевозможными стационарными движениями всех частиц коллектива, составляющего материальную систему. Конечно же, квантовое фазовое пространство – дискретное абстрактное математическое множество.

Статистическая термодинамика устанавливает связь между макроскопическими свойствами системы и свойствами образующих систему частиц, основываясь на законах механики и теории вероятностей. Статистическая термодинамика рассматривает механику большого числа частиц. Механические переменные выступают как случайные величины с определенными вероятностями появления. Термодинамические величины рассматриваются либо как средние значения случайных величин (например, внутренняя энергия системы, находящейся в тепловом контакте с окружением), либо как характеристики распределения вероятностей (температура, энтропия, химический потенциал). Статистическая термодинамика объясняет все положения классической термодинамики, а также дает возможность разрабатывать методы расчета термодинамических функций и констант равновесия на основе получаемых опытным путем молекулярных характеристик.

Все молекулы, составляющие какую-либо систему, отличаются друг от друга своим положением в пространстве, т.е. значениями координат, а также скоростями движения и энергиями. Если считать, что эти величины могут меняться непрерывно, то любому макросостоянию будет соответствовать бесконечно большое число микросостояний.

Для описания положения частицы используется понятие фазового пространства – воображаемого многомерного пространства, координатами которого являются декартовы координаты атомов и проекции импульса (р = mv) на трехмерные координатные оси. Для одноатомной молекулы фазовое пространство имеет шесть координат – три координаты положения x, y, z и три проекции импульса на координатные оси р_х, р_у, р_z. Для n-атомной молекулы требуется 6n величин, а фазовое пространство в этом случае будет 6n-мерным.

Каждая молекула системы изображается точкой фазового пространства, а микросостояние системы характеризуется набором таких точек.

Фазовое пространство разбивается на отдельные ячейки – столь малые области, чтобы изменение координат в пределах одной области не могло изменить данного микросостояния. Подсчет числа микросостояний, т.е. термодинамической вероятности состояния, в этом случае сводится к нахождению числа возможных способов размещения всех молекул по различным ячейкам фазового пространства.

Конкретное вычисление термодинамической вероятности зависит от дальнейших допущений об областях и частицах. По классической статистике Больцмана размер областей неопределенен, частицы различимы (их можно пронумеровать), а их энергетический спектр непрерывен. В квантовых статистиках учитывается, что возможные состояния системы могут быть только дискретными, и на способы распределения влияет спиновое число частиц. Для тождественных частиц с полуцелым спином (фермионов) выполняется запрет Паули: в заданном квантовом одночастичном состоянии может находиться не более одной частицы. Для частиц с нулевым или целым спином (бозонов) ограничения на способы заполнения состояний отсутствуют. Различия фермионов и бозонов приводят к тому, что ансамбли этих частиц подчиняются разным статистикам: Ферми –Дирака (для фермионов) и Бозе – Эйнштейна (для бозонов). Однако, вдали от абсолютного нуля молекулярные системы ведут себя практически одинаково, независимо от того, составлены они из бозонов или фермионов, а их особенности не проявляются в распределении. В таких случаях при подсчете квантовых состояний формально допустимо описывать систему как образованную пронумерованными частицами, рассматривать способы распределения частиц по ячейкам фазового пространства как для классических частиц по статистике Больцмана, но вводить поправку на неразличимость тождественных частиц с помощью множителя 1/N!. Тогда термодинамическая вероятность состояния системы, состоящей из N частиц, равна

W = 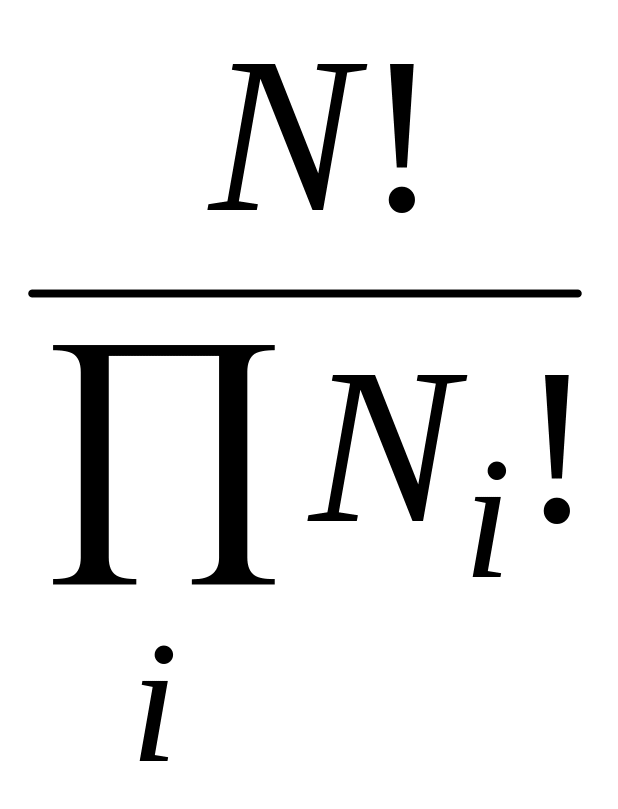, (2.1)

где ПN_і! – произведение факториалов числа частиц, находящихся в каждой ячейке фазового пространства.

По формуле Стирлинга, справедливой для больших N,

lnN!  NlnN – N (2.2)

или

N!  N^Nе^–N. (2.3)

Подставив это значение в уравнение (1.1), получим:

W = . (2.4)

Поскольку N_i = N, то = е^–N и

W = . (2.5)

Если подставить это выражение в формулу Больцмана, то получим для энтропии:

S = klnW = k(NlnN – N_ilnN_i). (2.6)

Основной целью статистического метода является установление количественной связи между характеристиками механических движений отдельных частиц, составляющих равновесный статистический коллектив, и усреднёнными свойствами этого коллектива, которые доступны для термодинамических измерений макроскопическими методами.

Цель состоит в том, чтобы на основании механических характеристик движений отдельных микроэлементов равновесного коллектива вывести количественные законы для термодинамических параметров системы.