Сумма по состояниям
Математическая вероятность w каждого из микросостояний, входящих в макросостояние, это его доля во всём ансамбле, то есть доля в макросостоянии. Она обратна термодинамической вероятности w =1/W и меньше единицы w <1.
Математические вероятности можно нормировать:
(4.1)
Всем микросостояниям отвечает одинаковая свободная энергия A, и поэтому множитель с нею можно вынести за знак суммы:
(4.2)
Второй сомножитель содержит сумму всех факторов Гиббса. Его называют суммой состояний, или суммой по состояниям, или статистической суммой исследуемого статистического коллектива (термодинамической системы) и обозначают как
(4.3)
Получаются очевидные соотношения,
;
(4.4)
Вероятность микросостояния
это одно из слагаемых суммы, и его можно
выделить
;
(4.5)
Часто применяется форма канонического распределения:
;
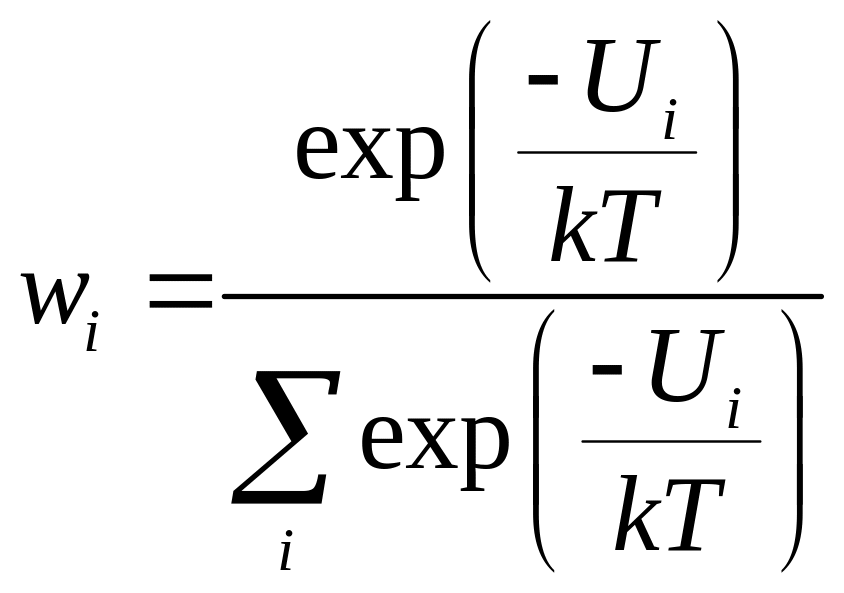(4.6)
Каноническое распределение по состояниям.
Запишем основную формулу:
(4.7)
Если у нескольких микросостояний энергии равны, то они относятся к общему вырожденному энергетическому уровню, а их вероятности одинаковы.
В этом случае удобно ввести кратности вырождения уровней gi. Объединяя равные слагаемые в формуле, статистическую сумму выражают через уровни:
;
(4.8)
Получают распределение по уровням.
Оно очень удобно для анализа квантовых стационарных движений.
Рассмотрим равновесную
изолированную систему, состоящую из N
молекул. По закону распределения
Больцмана число молекул Ni,
обладающих энергией i,
пропорционально фактору Больцмана,
равному
(k –
постоянная Больцмана):
Ni = А , (4.9)
где А – постоянная.
Общее число молекул равно
N = Ni = А (4.10)
или
N = Ni = АZ (4.11)
где
Z = (4.12)
называется статистической суммой по состояниям.
Из уравнений (4.9) и (4.11) получим отношение
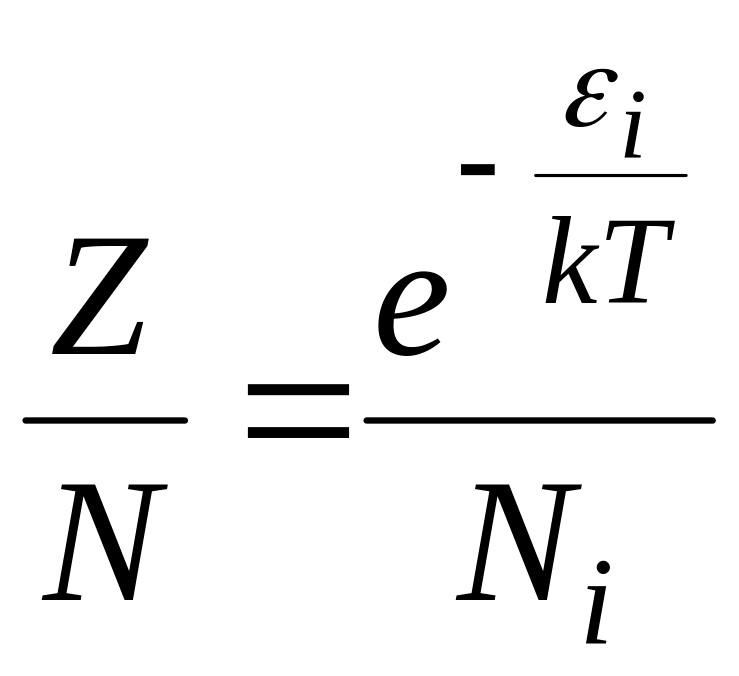, (4.13)
которое показывает, что сумма по состояниям так относится к полному числу молекул, как фактор Больцмана к числу молекул, обладающих заданной энергией.
Важным свойством суммы по состояниям является ее мультипликативность, т.е. общая сумма по состояниям может быть представлена как произведение сумм по состояниям, соответствующих отдельным независимым видам движения:
Z =
. (4.14)
Рассмотрим, например, случай, когда общая энергия молекул равна
i = пост,j + об,q. (4.15)
Тогда
Е =
=
ZпостZоб. (4.16)
Вместо абсолютного значения
энергии i
можно пользоваться энергией
=
i
– о,
отсчитанной от уровня энергии о
при абсолютном нуле
температуры (нулевая энергия). Тогда
уравнение (2.12) запишем в виде
Z =
, (4.17)
откуда
Z = Z
. (4.18)
В молекуле может быть несколько уровней с одинаковой или очень близкой энергией. Такие кратные уровни называются вырожденными. В этом случае одной и той же энергии отвечает несколько состояний молекулы, отличающихся не энергией, а каким-либо другим свойством (например, ориентацией магнитного момента).
Существование вырожденных уровней приводит к появлению в уравнении суммы по состояниям одинаковых членов, и эта сумма приобретает вид:
Z = qі , (4.19)
где qі – число совпадающих сомножителей для уровня i, которое называется вырожденностью уровня, или его статистическим весом.