1.2. Аксиомы статики

В основе статики лежит ряд основных положений, полученных в ре­зультате наблюдений, опыта и практической деятельности людей. На ос­новании этих положений, называемых аксиомами статики, путем строгих математических доказательств делаются все последующие выводы.

1 аксиома статики, получившая название аксиомы инерции, за­ключается в следующем:

Аксиома 1. Изолированная материальная точка находится в состоя­нии покоя или движется равномерно и прямолинейно.

Согласно этой аксиоме, материальная точка может двигаться равно­мерно и прямолинейно без приложенной к ней силы (по инерции). Изме­нить состояние покоя или равномерного прямолинейного движения мате­риальной точки может только сила.

Упомянутые два состояния точки объединяются в общем понятии "равновесие".

Аксиома 2. Две силы, приложенные к твердому телу, взаимно урав­новешиваются только тогда, когда они равны по величине и направлены по одной прямой в противоположные стороны (рис. 1.1).

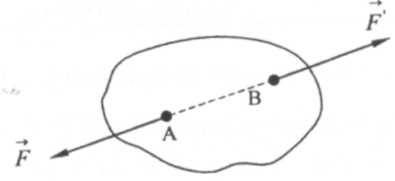Из этой аксиомы и рис. 1.1. следует, что при равновесии рассмат­риваемого тела F = F Рис. 1.1

Аксиома 3. Две силы, приложенные к твердому телу в одной точке, имеют равнодействующую, приложенную в этой же точке и изображаются диагональю параллелограмма, построенного на этих силах, как на сторонах.

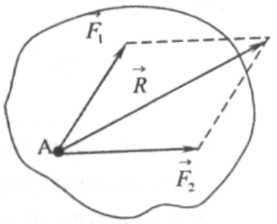На рис 1.2 показана равнодействующая R двух сил F₁ и F₂, при­ложенных к твердому телу в точке А. Операция замены системы сил её равнодействующей называется сложени­ем данной системы сил.

Мы видим, что сложение двух сил, приложенных к твердому телу в одной точке, подчиняется правилу векторного сложения, чем подтверждается вы­сказанное предположение о том, что сила есть вектор.

Таким образом, равнодействующая двух сил, приложенных к твердому телу в одной точке, равна их векторной сумме, т.е. ¯R = ¯F₁+¯F₂. (1.1)

Аксиома 4. Присоединение или отбрасывание взаимно уравновеши­вающихся сил не изменяет действия данной системы сил на твердое тело.

Например, если Q=Q, то системы сил, показанные на рис. 1.3, ста­тически эквивалентны, так как на основании аксиомы 2 силы Q и Q^/ вза­имно уравновешиваются и, следовательно, в силу аксиомы 4, их можно присоединить или отбросить.

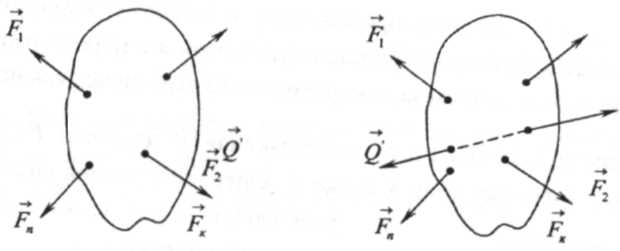
Рис. 1.3

Аксиома 5. Если каждая из двух систем статически эквивалентна одной и той же третьей системе, то они статически эквивалентны между собой. Понятно, что если система сил А статически эквивалентна системе С, и в то же время система В статически эквивалентна системе С, то и сис­темы А и В статически эквивалентны одна другой.

Из приведенных аксиом вытекают следующие следствия.

Следствие 1. Не изменяя действия силы на твердое тело, можно пе­реносить её точку приложения вдоль линии действия на любую точку тела.

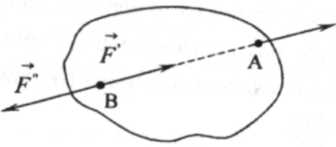
Рис. 1.4

В самом деле, три одинаковые по модулю силы F , F ^/ и —► F ^{? /} (рис. 1.4), направленные вдоль прямой, проходящие через точки А и В, статически эквивалентны, с одной стороны, силе F, так как силы F и F" взаимно уравновешиваются, и с другой стороны, силе и F , так как уравновешиваются силы F и F'^/ . Следовательно, статически эквивалентны силы F и F"', т.е. точку А приложения силы F можно переносить вдоль её линии в любую точку В твердого тела.

Такие векторы, которые по их физическому смыслу можно перено­сить вдоль прямых, по которым они направлены, называются скользящими векторами.

Следовательно, сила есть вектор скользящий.

Следствие 2. Сила ¯R (рис. 1.5) равная по модулю равнодействующей ¯R и направленная по одной с ней прямой в противоположную сторо­ну, уравновешивает данную систему сил.

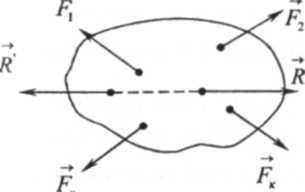Поскольку сила R^/ уравновешивает равнодействующую R, то она уравновешивает и статистически экви­валентную ей систему сил. F₁ F₂ ….F_n

Шестая аксиома, называемая аксиомой действия и противодействия, заключается в следующем:

Аксиома 6. Силы взаимодействия любых двух материальных объек­тов всегда равны по величине и направлены по одной прямой в противопо­ложные стороны.

¯ F¯ F^?¯ Эта аксиома, сформулированная Ньютоном, означает, что если объект А (рис. 1.6) действу­ет на объект В и это действие выражается силой F , то объект В оказывает объекту А противодействие, выраженное силой F^/ , причем F = - F'.

Таким образом, всякой силе, приложенной к некоторому материаль­ному объекту, соответствует равная ей по модулю и прямо противополож­ная по направлению сила, приложенная к другому объекту, взаимодействующему с данным. Подчеркнем, что силы действия и противодействия не уравновешивают друг друга, так как они приложены к различным объектам.

Седьмая аксиома называется аксиомой отвердения. Она заключается в следующем:

Аксиома 7. Если нетвердое тело находится в равновесии под дейст­вием приложенных к нему сил, то равновесие его не нарушается при его отвердении.

Из этой аксиомы следует, что если нетвердое тело находится в равновесии под действием прило­женных к нему сил, то под действием этой же системы сил будет находиться в равновесии и Рис. 1.7 соответствующее абсолютно твердое тело.

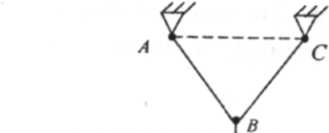Например, если нить ABC (рис. 1.7), закрепленная в точках А и С, находится в равновесии под действием приложенной к ней вертикальной

силы F, то под действием этой же силы будет находиться в равновесии и абсолютно твердое тело, имеющее такую же форму. Обратное заключение сделать нельзя, т.е. из того, что под действием некоторой системы сил на­ходится в равновесии абсолютно твердое тело, вовсе не следует, что под действием этой же системы сил будет находиться в равновесии и любое нетвердое тело.

Например, если к нити, показанной на рис. 1.7 приложить в. точке В силу, направленную по вертикали вверх, то она не будет находиться в рав­новесии, тогда как соответствующее абсолютное твердое тело и в этом случае будет находиться в равновесии.

Из этого следует, что вместо равновесия реально сущест­вующих тел, можно рассматривать равновесие соответствующих абсолют­но твердых тел.

Этими аксиомами и следствиями из них мы будем пользоваться при изложении последующих тем статики, в которых рассматриваются различ­ные виды систем сил, приложенных к материальному объекту.

Простейшей из таких систем является система сходящихся сил.