4.10. Задача выпуклого программирования

Пусть дана система неравенств следующего вида и функция Z

                               ,                                             (4.3)

,                                                 (4.4)

причем все функции  является выпуклыми на некотором выпуклом множестве , а функция  либо выпукла на множестве , либо вогнута. Задача выпуклого программирования (ВП) состоит в отыскании такого решения системы ограничений (4.3), при котором целевая функция  достигает минимального значения, или вогнутая функция  достигает максимального значения. (Условия неотрицательности переменных можно считать включенными в систему (4.3)).

Множество точек называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий эти точки. Если  — отрезок на числовой прямой и , то ,  или

, , , .                                                (4.5)

Нетрудно видеть и обратное: если выполняется (4.5), то . Таким образом, отрезок можно определить как множество всех точек , удовлетворяющих условию (4.5). Тогда выпуклое множество — это множество, которое вместе с любой парой своих точек ,  содержит и все точки , для которых выполняется (4.5). Эти определения отрезка и выпуклого множества сохраняются для случая, когда , ,  — точки n-мерного пространства (где операции в равенстве (4.5) выполняются покоординатно).

Исходя из равенства (4.5), по индукции можно показать, что если   — выпуклое пространство, то  для любых точек  и любых действительных чисел , удовлетворяющих условию .

Функция , определенная на выпуклом множестве    п-мерного пространства, называется выпуклой на этом множестве, если

                                        (4.6)

для любых точек и любого числа .

Если в условии (4.5) изменить знак неравенства  на , то получим определение вогнутой функции. Если же в условии (4.6) неравенство выполняется как строгое, то функция называется строго выпуклой (или строго вогнутой).

На рис. 4.3 изображен график функции одной переменной, выпуклой на всей числовой прямой.

Для любой пары  ,  значений аргумента произвольную точку   можно задать в виде  . Как видно из рис. 4.3, неравенство (4.6) означает, что отрезок, соединяющий точки   и   расположен не ниже графика функции на этом участке (для строго выпуклой функции этот отрезок лежит выше графика). Таким образом, выпуклость или вогнутость функции одной переменной сразу же видна по ее графику.

Пример. Геометрически решить следующую задачу ВП: найти минимум функции  при ограничениях:

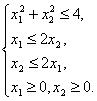
Решение. Строим область допустимых решений данной задачи:

а)      — окружность с центром в начале координат и радиусом       R = 2.   (рис. 11.3). Область решений неравенства  состоит из точек, лежащих внутри этой окружности и на ней самой;

б)       — прямая, которую можно построить, например, по точкам  и . Область решений неравенства  - полуплоскость, лежащая над этой прямой, включая и саму прямую;

в)       — прямая, которая строится, например, по точкам  и . Область решений неравенства — полуплоскость, лежащая под этой прямой, включая и саму прямую. Таким образом, с учетом условий неотрицательности переменных, областью допустимых решений данной задачи является замкнутый сектор  (рис. 4.4).

Теперь построим линию уровня функции  и определим направление убывания . Все линии уровня имеют равнение , т.е. . При  получаем линию уровня  - это окружность с центром в точке и радиусом . Ясно, что в любой точке этой линии уровня при перемещении от

центра окружности  функция  возрастает, а при перемещении к центру — убывает. Таким образом, минимум  достигается в точке ,  (нетрудно убедиться, что точка  является стационарной точкой функции ).