3.3. Задача о разорении. Вероятность разорения
Рассмотрим состояние страхового портфеля не только в конце более длинных периодов времени (чем год), но и в промежуточные моменты времени, вне зависимости от того, предъявляются ли страховой компании требования о выплате. В частности, обсудим вопрос: имеются ли у компании достаточные средства для того, чтобы оплатить потенциальные требования о выплате?
Сумма, которую компания имеет в момент времени t, называется активами на момент t. Ясно, что
[Активы на момент t] = [Исходные активы] + [Взносы на момент t] – [Выплаты на момент t] |
(3.1) |
Нашей целью будет определение вероятности разорения и ее зависимости от:
начальных активов;
надбавки безопасности.
Чтобы найти взаимосвязь предположим, что:
требования о выплате, предъявляемые страхователями, оплачиваются немедленно;
процентная ставка равна нулю;
издержки страховщика во внимание не принимаются
Пусть:
N(t) - число требований о выплате, имевших место до момента t; t>0.
{N(t)} 0t - случайный процесс, описывающий число требований о выплате.
Xi- размер i-й страховой выплаты.
S(t) - общий размер страховых выплат, имевших место до момента t, t>0.
{S(t)} 0t - случайный процесс, описывающий общий размер выплат.
Для каждого t>0 имеем:
,
U - начальные активы;
U(t) - активы страховщика в момент t.
Предположим, что страховые взносы поступают непрерывно и с фиксированной скоростью c. Тогда по (3.1) имеем
U(t)=U+ct-S(t)
Ясно, что {U(t)}t0 - случайный процесс, называемый процессом изменения активов.
Когда активы падают до нуля, то говорят, что произошло разорение страховщика.
(U) называется вероятностью окончательного разорения при данных начальных активах U:
(U)=Pr(u(t)<0, при некотором t, 0<t< )
3.4. Сложные пуассоновские процессы
Сложное пуассоновское распределение S ~ CP(l ,F), если
1. Xj одинаково распределены с общей для них функцией распределения F(x)
2. Xj независимы от N
3. N ~ P(l )
В этом случае
Введем дополнительные предположения:
а)
случайные величины
независимы
и одинаково распределены (обозначим
общую для всех Xi функцию
распределения через F(x), плотность
распределения через f(x));
б) случайные величины независимы от N(t) при всех t0;
в)
случайный процесс
является
пуассоновским с параметром ,
т.е.
Тогда процесс {S(t)}t 0 является пуассоновским процессом.
Обозначим
.
Предположим, что страховые взносы,
собранные страховщиком за единичный
момент времени, превосходят ожидаемую
величину страховых выплат за единицу
времени
C можно записать в терминах относительной надбавки
Предположим, что Mx(t) - производящая функция моментов для распределения страховых выплат.
3.5. Неравенство Лундберга
Обычно невероятно трудно вычислить точно вероятность (окончательного) разорения (U).
Неравенство Лундберга дает некоторую верхнюю границу для (U):
(U)
|
(3.2) |
exp(-RU)где R - поправочный коэффициент;
U - начальные активы.
Это неравенство имеет два преимущества над точным выражением для (U):
1) его просто применять;
2) если U не слишком малы, то достигаемая аппроксимация очень хорошая.
Неравенство (3.2) говорит о том, что вероятность разорения ограничена функцией, экспоненциально убывающей с ростом U. Вероятность разорения убывает с ростом U и R.
Поправочный коэффициент R является единственным положительным корнем уравнения
|
(3.3) |
Уравнение (3.3) обычно решается численно (например, используется метод Ньютона).
Пример 1. Распределение выплат экспоненциально с функцией распределения F(x)=1-exp(- x), x>0. Найти поправочный коэффициент.
Решение. Производящая функция моментов M(t)= /( -t), а среднее p1=1/, то нужно решить уравнение
Тогда поправочный коэффициент равен
Если (3.3) решается с помощью численных методов, то верхняя граница для R может оказаться очень полезной. Из (3.3) получаем
откуда
|
(3.4) |
Зависимость поправочного коэффициента от надбавки безопасности представлена на рис 3.2.; первый график соответствует экспоненциальному распределению со средним 1, а второй - постоянному распределению страховых выплат (каждая страховая выплата имеет размер 1).
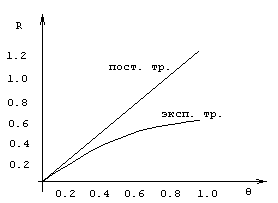
Рис 3.2. График зависимости R от .