39.Пути интенсификации теплопередачи.

И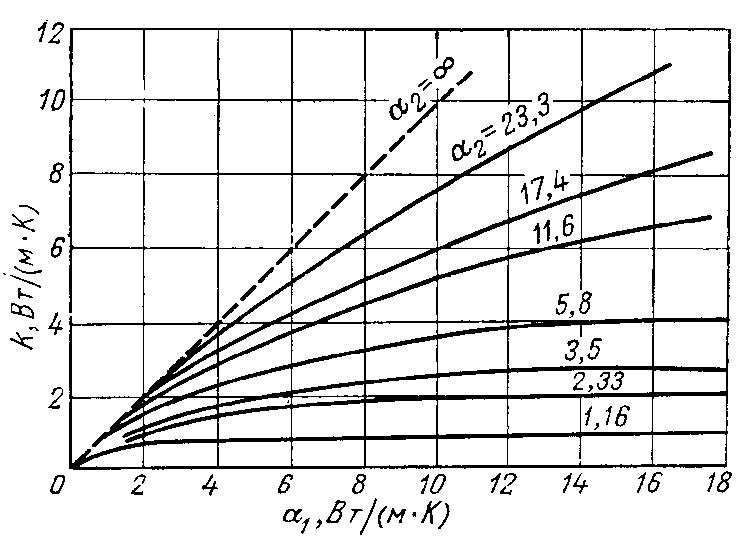 нтенсификация теплопередачи путем увеличения коэффициента теплоотдачи. Из уравнения теплопередачи следует, что при заданных размерах стенки и температурах жидкостей величиной, определяющей теплоотдачу, является k. Но поскольку теплопередача – явление сложное, то правильное решение можно найти на основе анализа частных составляющих, характеризующих процесс. Например, если мы имеем дело с плоской стенкой, для которо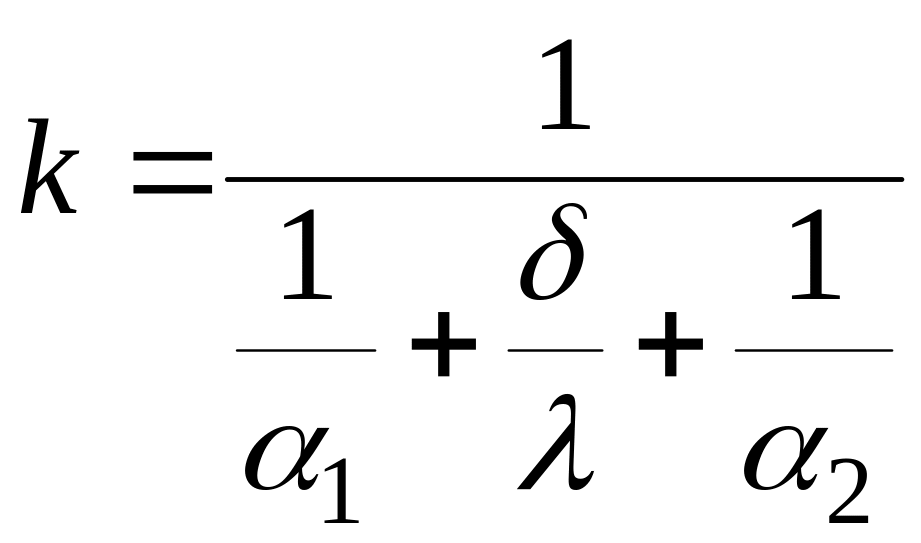й ,то при (что можно принять для тонких стенок с большим коэффициентом λ) 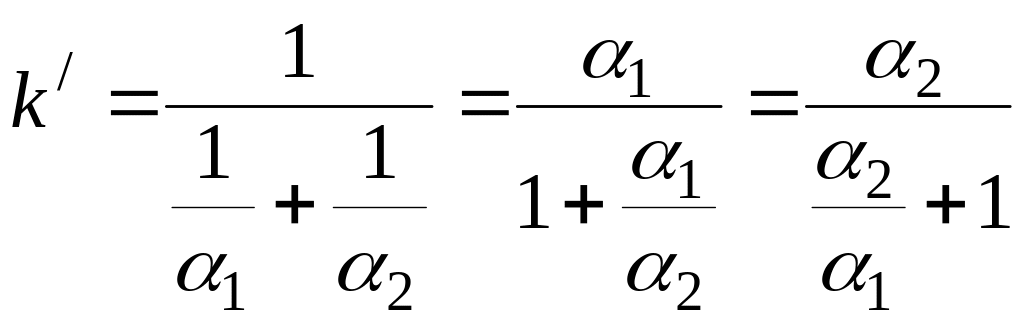. следует, что коэффициент теплопередачи не может быть больше самого малого α. При k^/ стремиться к своему предельному значению α₁. При коэффициент теплопередачи стремиться к . при α₁<<α₂ увеличение боль­шего из коэффициентов теплопередачи (α₂) практически не дает увели­чения . Увеличение меньшего из коэффициентов теплоотдачи (α₁) в 2 и 5 раз дает увеличение k' почти во столько же раз. при α₁<<α₂ увеличение k' возможно только за счет увеличения α₁. Если α₁≈α₂ увеличение коэффициента теплопередачи возможно за счет увеличения любого из α.

Интенсификация теплопередачи за счет оребрения стенок

При передаче теплоты через цилиндрическую стенку термические сопротивления и определяются не только значениями ко­эффициентов теплоотдачи, но и размерами самих поверхностей. При передаче тепла через шаровую стенку влияние диаметров d₁ и d₂ ока­зывается еще сильнее, что видно из соотношений и . Такой же результат можно получить и для плоской стенки, если одну из поверхностей увеличить путем оребрения. и .Следует указать, что при использовании метода оребрения нужно руководствоваться следующими соображениями: если α₁<<α₂, то оребрять поверхность со стороны α₁ следует до тех пор, пока не дости­гает значения . Дальнейшее увеличение поверхности F₁ малоэффек­тивно. Строгое аналитическое решение задачи о распространении теплоты в ребре связано со значительными трудностями. В основу решения по­этому кладут некоторые допущения, которые позволяют сравнительно простым путем получить нужный результат. Ниже рассмотрим метод решения задач о теплопроводности в ребрах простейших геометрических форм.

41.Дифферинциальные уравнения конвективного теплообмена: уравнения теплоотдачи, энергии, движения, неразрывности.

Из уравнения

следует, что плотность теплового потока в любой точке жидкости для каждого момента времени однозначно определяется, если известны поля температур, удельной энтальпии и скорости.

Связь между температурой и энтальпией может быть установлена следующим образом. Для реальной жидкости , и согласно понятию о полном дифференциале .

Отсюда .

При C_p=const

Температурное поле движущееся в жидкости определяется из уравнения энергии .

x, y, z – соответствующие скорости.

Поле скоростей, движущейся жидкости можно определить из уравнений движения, которые в векторной форме, записываются в виде:

.

Так как в уравнение движения, помимо входит еще неизвестная величина р, то система уравнений не является замкнутой. Необходимо добавить еще одно уравнение. Таким уравнением является дифференциальное уравнение сплошности (неразрывности).

(4.20)

Записав к этим уравнениям условия однозначности, которые дают математические описания всех частных особенностей данного процесса и решив эту систему получим значения температурного поля в движущейся жидкости, определим коэффициент теплоотдачи:

Зная ,

42.Критерии подобия креториальные уравнения.

В общем случае коэффициент теплоотдачи

Для того что бы переменных влияющих на процесс конвективного теплообмена эти размерные величины объединяют в безразмерные комплексу число которых значительно меньше размерных величин что позволяет упростить эти задачи.

Первый из этих безразмерных комплексов обозначают

и называют числом Нуссельта или безразмерным коэффициентом теплоотдачи. Число Нуссельта характеризует теплообмен на границе стенка – жидкость. В задачах конвективного теплообмена число Nu обычно является искомой величи­ной, поскольку в него входит определяемая величина α.

Безразмерный комплекс

называют числом Рейнольдса. Оно характеризует соотношение сил инерции и сил вязкости.

Безразмерный комплекс

называют числом Грасгофа. Оно характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей.

Безразмерная величина представляет собой новую перемен­ную, называемую числом Прандтля. Число Прандтля целиком со­ставлено из физических параметров, и поэтому и само является физи­ческим параметром. Его можно записать и в виде

Имеет смысл подобие температур и скоростей.

Используя эти критерии можно получить уравнение для определения коэффициента теплоотдачи