
- •Глава 1
- •§ 1.1. Радиоприемное устройство как составная часть радиосистемы
- •§ 1.2. Структурные схемы радиоприемников
- •§ 1.3. Основные характеристики радиоприемников
- •Глава 2
- •§ 2.1. Сигналы на входе приемника, прошедшие однолучевои канал
- •§ 2.2. Сигналы на входе приемника, отраженные пространственно-распределенными рассеивателя ми
- •§ 2.3. Внутренние шумы приемников
- •§ 2.4. Внешние шумы
- •§ 2.5. Коэффициент шума и шумовая температура
- •§ 2.6. Расчет реальной чувствительности радиоприемного устройства
- •Глава 3
- •§ 3.1. Входные цепи
- •1. Коэффициент передачи по напряжению
- •§ 3.2. Транзисторные усилители радиочастоты
- •§ 3.3. Регенеративные мшу диапазона свч
- •§ 3.4. Полупроводниковые параметрические усилители
- •§ 3.5. Усилители на туннельных диодах
- •Глава 4
- •§ 4.1. Основные показатели и типы упч
- •§ 4.2. Упч с распределенной избирательностью
- •§ 4.3. Упч с сосредоточенной избирательностью
- •§ 4.4. Упч с дискретными и цифровыми фильтрами
- •Глава 5
- •§ 5.1. Общая теория преобразования частоты
- •§ 5.2. Побочные каналы приема
- •§ 5.3. Преобразователи частоты на полевых и биполярных транзисторах
- •§ 5.4. Преобразователи частоты на интегральных микросхемах
- •§ 5.5. Диодные преобразователи частоты
- •§ 5.6. Гетеродины
- •Глава 6
- •§ 6.1. Параметры
- •§ 6.2. Принципы построения и функциональные схемы свч-модулей
- •§ 6.3. Гибридно-интегральные свч-модули
- •Глава 7
- •§ 7.1. Задачи, решаемые детекторами сигналов. Основные характеристики детекторов
- •§ 7.2. Амплитудные детекторы
- •§ 7.3. Ограничители амплитуды
- •§ 7.4. Фазовые детекторы
- •§ 7.5. Частотные детекторы
- •Глава 8
- •§ 8.1. Принципы автоматической регулировки усиления. Разновидности систем ару
- •§ 8.2. Элементы систем ару
- •§ 8.3. Работа ару
- •§ 8.4. Динамика систем ару
- •Глава 9
- •§ 9.1. Принципы автоматической подстройки частоты. Разновидности систем апч
- •§ 9.2. Элементы систем апч
- •§ 9.3. Переходные процессы
- •§ 9.4. Устойчивость систем апч
- •Глава 10
- •§ 10.1. Области применения и принципы работы системы фапч
- •§ 10.2. Дифференциальное уравнение
- •§ 10.3. Статистические характеристики системы фапч и ее модели
- •§ 10.4. Использование
- •§ 10.5. Цифровые системы фапч
- •Глава 11
- •§ 11.1. Радиоприем
- •§ 11.2. Оптимальный радиоприем в аддитивном гауссовом белом шуме
- •§ 11.3. Оптимальная нелинейная фильтрация сообщений
- •Глава 12
- •§ 12.1. Структурные схемы радиоприемников импульсных сигналов
- •§ 12.2. Особенности линейного тракта радиоприемника импульсного сигнала
- •§ 12.3. Прохождение импульсного сигнала через линейную часть радиоприемника
- •§ 12.4. Согласованные
- •§ 12.5. Согласованные фильтры и конвольверы на пав
- •Глава 13
- •§ 13.1. Особенности иас
- •§ 13.2. Структурная схема приемника иас
- •§ 13.3. Квазикогерентные демодуляторы квантованных вим-и чим-смгналов
- •§ 13.4. Квазикогерентный приемник ким-сигналов
- •§ 14.1. Структурная схема приемника дискретных сигналов
- •§ 14.2. Квазикогерентные демодуляторы двоично-манипулированных сигналов
- •§ 14.3. Некогерентные демодуляторы двоично-маиипулироваииых сигналов
- •Глава 15
- •§ 15.1. Общие сведения о приеме непрерывных сигналов и сообщениях
- •§ 15.3. Прохождение ам-сигнала через линейную часть приемника
- •§ 15.4. Приемники чм-и фм-сигналов
- •9Ш(0 y(t)iAlt.
- •§ 15.5. Прохождение чм (фм)-сигнал а через линейную часть приемника
- •§ 15.6. Приемники чм-сигнала с обратным управлением
- •§ 15.7. Приемники однополосных сигналов
- •Глава 16
- •§ 16.1. Особенности приема сигналов в оптическом диапазоне
- •§ 16.2. Приемные устройства
- •§ 16.3. Приемные устройства
- •Глава 17
- •§ 17.1. Задачи и организация математического моделирования
- •§ 17.2. Методы математического моделирования (методы составления математических моделей)
- •§ 17.3. Методы составления цифровых моделей (методы оцифровывания математических моделей)
- •§ 17.4. Математическое моделирование рпу методом несущей
- •§ 17.5. Математическое моделирование рпу методом комплексной огибающей
- •§ 17.6. Математическое моделирование рпу методом статистических эквивалентов
- •§ 17.7. Математическое моделирование рпу методом информационного параметра
- •17. Кривицкий б. X., Салтыков е. Н.
- •29. Тихонов в. И., Кульман н. К.
§ 7.5. Частотные детекторы
В частотных детекторах (ЧД) ЧМ-колебание преобразуется в колебание, модулированное по амплитуде, фазе или в импульсно-модулирован-ное колебание с последующим применением амплитудного, фазового или пикового детекторов. При этом для неискаженного воспроизведения модулирующей функции детекторная характеристика должна обладать достаточной линейностью в диапазоне изменения мгновенной частоты сигнала. Для частотных детекторов, используемых в системах автоподстройки частоты, необходимо, чтобы детекторная характеристика проходила через нуль на некоторой центральной частоте /0. Фиксация этой частоты может осуществляться либо резонансными цепями, входящими в схему ЧД, либо с помощью специального высокостабильного генератора.
Рассмотрим разновидности частотных детекторов в соответствии с осуществляемыми в них видами преобразования частотной модуляции и способами фиксации центральной (переходной) частоты.
Частотные детекторы с амплитудным преобразованием частотной модуляции. Принцип действия таких ЧД основан на том, что при прохождении ЧМ-колебания через дифференцирующую цепь выходное колебание приобретает дополнительную амплитудную модуляцию, причем закон изменения амплитуды полностью повторяет закон изменения частоты. Пусть "вх(0 - с7вх sin \w0t ! <г(/)1. Тогда на выходе дифференцирующей цепи с коэффициентом передачи Кл„,\,
![]()
Подав это напряжение на амплитудный детектор, получим на его выходе напряжение U_(t) = ЛГдс7вхх
X Кд/СдИф), пропорцио-
нальное изменению частоты. Струк-
турная схема подобного ЧД легко реализуется средствами современной микроэлектроники. Например, дифференцирующая цепь может быть выполнена на операционном усилителе (ОУ) с линейной обратной связью, а амплитудный детектор — на операционном усилителе с нелинейной обратной связью. Диапазон рабочих частот указанных ЧД ограничен частотными свойствами ОУ.
С позиций частотных представлений идеальная дифференцирующая цепь имеет коэффициент передачи К (/<о) у ют (для резонансных цепей К (/<•>) / ("> ft>o) т)- модуль которого является прямой, проходящей с угловым коэффициентом т к оси частот. На основе такого представления можно построить ЧД, используя, скаты частотных характеристик RC-, RL и RLC-цепей, выбирая на них относительно линейные участки. Простейшая схема подобного детектора ЧМ изображена на рис. 7.35. Комплексный коэффициент усиления резонансного усилителя, входящего в частотный детектор, с учетом выходного сопротивления и емкости транзистора Т. а также входного сопротивления и емкости амплитудного детектора на диоде Д можно определить из выражения
![]() (7.58)
(7.58)
Здесь | (///„ — /„//') daK — обобщенная расстройка; 4ЯИ " 1/м„С2/? ,|;: Сх Ск '■ Свых /i," Свх/;-; 5„ крутизна транзистора (полагается что /» <■'.' fs', fs — граничная частот'
транзистора по крутизне); R9K =^ <Як II«; #ВЬ1х 11#вх/лЦ) — эквивалентное резонансное сопротивление контура; л,, п.г— коэффициенты трансформации при подключении транзистора и детектора к контуру; К» 50/?чкп2//г, — резонансный коэффициент усиления.
В предположении линейности амплитудного детектора выпрямленное напряжение

(7.59)
Уравнение (7.59) описывает детекторную характеристику, которая по форме повторяет амплитудно-частотную характеристику резонансного усилителя (рис. 7.36). На скатах этой характеристики можно выбрать относительно линейные участки, пригодные для осуществления частотного детектирования (отмечены на рис. 7.36 жирными линиями). Крутизна детекторной характеристики в координатах £/_, £ изменяется по закону
![]()
(7.601
и имеет максимальное значение npi-расстройках £т — ±0,7. Практиче ски подобный простейший частотны» детектор применяют только в систе мах с узкополосной ЧМ, так как oi не обеспечивает высокой линейност* и крутизны детекторной характеристи ки. При этом выбирают £г = \/daKX X (/,.//,, /„//с) ~ 1- где /,. --- несу' щая частота сигнала.
В системах широкополосной ЧМ и АПЧ используют балансные ЧД с двумя расстроенными контурами. Схема такого ЧД с параллельными расстрое-енными контурами изображена на рис. 7.37. Контуры ЧД настроены на
частоты /01 и /и3, расположенные симметрично по обе стороны от центральной частоты /"„ = /с. Выпрямленные напряжения амплитудных детекторов, подсоединенных к контурам, включены встречно и выходное напряжение образуется как разность выпрямленных напряжений: ы_ — м_, — ы_2. Формирование детекторной характеристики ясно из рис. 7.38. Пунктиром изображены положительные полуволны детекторной характеристики при Е0 0,707; 2,0 (So So. IS021 -(/«,//« - /о //„,) Л*эн ^
* HUrfo - /*//м)/^.к1).
В предположении одинаковости резонансных сопротивлений контуров и коэффициентов передачи амплитудных детекторов на диодах Д1 и Д2 получаем следующее уравнение детекторной характеристики:
![]()
17.61)
В координатах l}_, | крутизна детекторной характеристики при £=0

и имеет максимальное значение при
So - Soopt 1 V2" 0,707.
Экстремумы детекторной характеристики расположены в точках \т
± £„. Заметим, что в координатах / крутизна детекторной характеристики

пускания чД (расстояние между экстремумами на оси частот), и вычисляя 5цд с подстановкой А\к т

Эта функция возрастает с увеличением |0, причем

(7.64)
Это означает, что при заданной полосе пропускания Д/чд и центральной частоте /„ увеличение крутизны Shjx может быть достигнуто снижением затухания контуров d3K, так как
£о == А/чд/^эк/о-
Практически снижать затухание контуров целесообразно до значений, при которых |0 = 2 -т- 3, так как дальнейшее уменьшение d9K приводит к очень медленному росту 5чд.
Частотные детекторы с фазовым преобразованием частотной модуляции. В ЧД этого типа частотная модуляция преобразуется в фазовую и используется фазовый детектор для выделения модулирующей функции.
Принцип действия таких ЧД основан на том, что при прохождении ЧМ-колебания через цепь, вносящую идеальную задержку, фазовый сдвиг выходного колебания относительно входного, которое выполняет в данном случае роль опорного напряжения, повторяет закон изменения частоты. Действительно, пусть на входе цепи, вносящей задержку т, действует ЧМ-колебание ивх — U0 sin [со„/ + +ф (г)], частота которого изменяется по закону со (t) — со,, + dcp/df. Тогда на выходе этой цепи имеем
«вых tV0 sin [со,, (/— т) + ф (/- т)].
Фазовый сдвиг выходного напряжения относительно входного
изменения фазы чм-колеоания на выходе линии задержки относительно входного ЧМ-колебания совпадает с законом изменения частоты. .
На основе такого представления можно построить ЧД, используя относительно линейные участки фазо-частотных характеристик четырехпо-

люсников, так как в пределах этих участков задержка примерно постоянна. Структурная схема подобного ЧД представлена на рис. 7.39. Здесь через К (/со) обозначен комплексный коэффициент передачи четырехполюсника. В схему рис. 7.39 включен также фазовращатель на ф = 90°. При Ф = 90° детекторная характеристика ФД проходит через нуль (см. рис. 7.31), благодаря чему переходная частота детекторной характеристики ЧД будет совпадать с резонансной частотой четырехполюсника К (/со), если этот четырехполюсник имеет резонансную АЧХ и вносит на резонансной частоте нулевой фазовый сдвиг. Однако если четырехполюсник К (/со) вносит на резонансной частоте фазовый сдвиг (2п + 1)-90°, где п -— 0, \, 2, то отдельного фазовращателя на ф = 90° не требуется (поэтому на рис. 7.39 он показан пунктиром).
В простейшем случае четырехполюсником К (/to) может быть, например, одиночный колебательный контур (или усилитель с одиночным контуром), фазовая характеристика которого описывается уравнением Ф(£) = - arctg £, I = Шэ„(т7/о-— /„//). Эта характеристика имеет почти линейный участок в области | да 0 и, следовательно, может быть использована для преобразования входного ЧМ-колебания в ФМ-ко-лебание на контуре.
Суммируя напряжение на контуре усилителя с опорным напряжением и подвергая результирующее напряжение амплитудному детектированию, получаем низкочастотное колебание, воспроизводящее закон изменения мгновенной частоты сигнала.

Н9
Пример подобной схемы ЧД приведен на рис. 7.40. Контур LKC„ связан с первичным контуром LrC, индуктивной связью М, кроме того, через разделительный конденсатор Cv на дроссель L подается полное напряжение с первичной катушки, являющееся опорным напряжением U„. Оба контура настроены на центральную частоту /0 и имеют одинаковые затухания dAK. Полное напряжение на лиоле
![]()
Анализ схемы приводит к следующему выражению для с7д:

где р = KcJd™ М/1/LtLKd3K — обобщенный коэффициент связи; R— резонансное эквивалентное сопротивление контура.
При наличии линейного амплитудного детектора с коэффициентом передачи К я

Уравнение (7.66) описывает детекторную характеристику рассматриваемого ЧД. Примерный вид ее изображен на рис. 7.41.
На практике обычно применяют балансные ЧД с фазовым преобразованием ЧМ. Схема подобного ЧД приведена на рис. 7.42. В нее входит балансный фазовый детектор, опорным напряжением для которого является напряжение на первичном контуре L,C,, действующее также на дросселе L. Поскольку нагрузки включены встречно, U_ - U -, - (/_,, Напряжения на диодах.

(7.67)
Этим векторным уравнениям соответствуют векторные диаграммы рис. 7.30, причем отклонение срс от я/2 обусловлено расстройкой контура LKCK. Уравнение детекторной характеристики получается как разность уравнений вида (7.66) с учетом того, что здесь напряжение сигнала на каждом диоде равно/У J2, а не (У к и для диода Д2 имеет место вычитание UJ2:
Вид детекторной характеристики и способ ее формирования иллюстрируются рис. 7.43. Параметром детекторной характеристики при UBX ~-
const является обобщенный коэффициент связи р. При р > 1 положение точек экстремума на оси абсцисс примерно соответствует величинам р, т. е. £m = ± р. Отсюда Д/чд да рД/0,7, где Д/0|7 = /od8„ — полоса пропускания одиночного контура ЧД без учета вносимого сопротивления.
Анализ уравнения (7.68) в области Е = О приводит к следующему выражению для крутизны детекторной характеристики:

Поскольку р = KcJd3K, это означает, что для увеличения крутизны характеристики при выбранном значении /С,:в следует уменьшать затухания контуров d3K, что эффективно при р < 3.
Если затухания контуров и центральная частота выбраны, то добиваться максимума крутизны следует выбором р. Анализ выражения (7.69) дает при этих условиях р = popt == = 0,85. Отметим, что усилительный прибор Т, в схемах рис. 7.35, 7.37, 7.40, 7.42 может работать в сугубо нелинейном режиме (амплитудный ограничитель) и тогда всюду вместо низкочастотного значения крутизны следует подставлять крутизну по первой гармонике выходного тока, т. е.
Для преобразования изменений частбты в изменения фазы можно непосредственно использовать линию задержки в качестве фазосдвигающе-ю четырехполюсника (см. рис. 7.39). В *том случае К (/to) — е^'",т. Иде-

Рис. 7.43
альная линия задержки имеет линейную фазовую характеристику ср (со) = = — сот, и, следовательно, при прочих равных условиях можно существенно снизить уровень нелинейных искажений. В зависимости от диапазона частот и технологии изготовления линия задержки может быть мик-рополосковой, коаксиальной, вол-новодной, на ПАВ, и т. д.
Воспользовавшись выражением для детекторной характеристики фазового детектора (7.50) при условиг сУ0 — с7с, получим
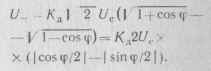
(7.7Г
Учитывая, что ср = сот, находил уравнение детекторной характеристи ки ЧД с линией задержки:
£/_ =2с7гА:д(|соя (сот/2) | —
— | sin (сот/2) |. (7.72
Вид детекторной характеристик! в координатах UJ2UcKp,\ toT/2 по казан на рис. 7.44. Частоты переход через нуль находят из соотношение со„т/2 = (1 4 2 А) л/4, k — 0, 1 2, ... .

Отсюда определяем необходимое время задержки для выбранной частоты
Л.:
![]() (7.73)
(7.73)
Представляя мгновенную частоту в виде со со,, ; Асо, получим уравнение детекторной характеристики в пределах одной ветви:
![]() (7.74)
(7.74)
Крутизна характеристики ЧД на частоте настройки
![]()
Из рис. 7.44 видно, что расстояние между точками излома функции ф (сот/2) составляет л/2, следовательно, полосу ЧД в пределах точек излома можно найти из условия Дсот/2 =* л/2, откуда
![]()
(7.76)
Как показывает более подробный анализ, достоинствами ЧД с линией задержки является примерно вдвое более широкая полоса детекторной характеристики по сравнению с ЧД на связанных и расстроенных контурах при одинаковом уровне нелиней-
ных искажений, а также в 3—5 раз меньшее время переходного процесса ввиду отсутствия резонансных контуров, что важно при детектировании импульсных ЧМ-сигналов.
Заметим, что во избежание появ-ния «изрезанное™» детекторной характеристики линия задержки должна быть тщательно согласована, т. е. не иметь отражений с обоих концов.
Частотные детекторы модуляционного типа. Подобные ЧД получили широкое распространение в диапазоне СВЧ как для демодуляции СВЧ-ко-лебаний, так и в качестве чувствительных элементов систем АПЧ по эталонному резонатору. В них используется контур (резонатор) с переменной частотой настройки (модулированный контур). Использование высокодобротного резонатора дает возможность получить стабильное значение центральной (переходной) частоты, а введение модуляции частоты настройки позволяет всю дальнейшую обработку выходного сигнала резонатора выполнить на низкой частоте модуляции и обеспечить выявление направления изменения мгновенной частоты входного сигнала.
На рис. 7.45 изображена частотная характеристика контура U (/).
Резонансная частота /р периодически изменяется с низкой частотой модуляции F в соответствии с кривой /р (/). Если частота входного сигнала расположена в точке а, т. е. / — /ро + -f-ДД то изменение частоты настройки контура вызовет изменение амплитуды напряжения на нем в соответствии с рис. 7.45,0. При нахождении частоты сигнала в точке б амплитудная модуляция будет соответствовать рис. 7.45, б, а в точке в — рис. 7.45, в.
Как видим, фаза огибающей изменяется на л при переходе частоты сигнала с одного ската частотной характеристики на другой. Если же частота сигнала соответствует центральному значению /р (/ро), то амплитудная модуляция сигнала осуществляется по кривой, в спектре которой отсутствует составляющая частоты модуляции (основная частота этой кривой равна 2 F). Таким образом, амплитуда составляющей частоты F в спектре огибающей свидетельствует об отклонении частоты сигнала от центрального значения fp (/р0), а фаза этой составляющей — о направлении отклонения (больше, меньше).
Анализ процессов, происходящих в модулированном контуре при условии F <g /р0, дает следующее приближенное выражение для относительной амплитуды первой гармоники огибающей (частоты F):

девиация резонансной частоты контура.
Графики, построенные по уравнению (7.77), приведены на рис. 7.46. Они имеют почти линейные участки в области 1 — 0, а крутизна зависит от относительной девиации резонансной частоты контура. Максимальная крутизна соответствует |m х 0,8. При меньших девиациях мала глубина AM, а при больших уменьшается содержание первой гармоники, так как захватывается большая часть ре-

Рис. 7.46
зонансной кривой, в том числе области, где амплитуда первой гармоники равна нулю.
Использование модулированного контура для построения ЧД возможно в соответствии со структурной схемой рис. 7.47. Входной сигнал поступает на модулированный контур МК, резонансная частота которого изменяется при подаче напряжения от гетеродина Г (варикап, феррит, вибрирующая мембрана в объемном резонаторе и т.д.). Огибающая АМ-коле-бания выделяется амплитудным детектором АД и усиливается усилителем огибающей УО. Последний одновременно фильтрует первую гармонику, отсеивая высшие составляющие. Напряжение с выхода УО продается на фазовый детектор ФД, причем в качестве опорного напряжения используются колебания модулирующего гетеродина.
Выходное напряжение ФД (в целом — ЧД) по значению пропорционально амплитуде первой гармоники огибающей (отклонению частоты сигнала от /ро), а по знаку соответствует фазе этой гармоники относительно фазы опорного напряжения.
Частотные детекторы с внутренним ограничением. Выходное напряжение ЧД пропорционально амплитуде
входного напряжения [см. выражения (7.59), (7.61), (7.66), (7.68)]. Поэтому при наличии во входном напряжении паразитной амплитудной модуляции (ПАМ) выходное напряжение ЧД будет определяться изменением не только частоты, но и амплитуды, что приведет к нелинейным искажениям. Во избежание этого перед ЧД ставят амплитудный ограничитель. Однако при этом необходимо увеличить усиление в тракте УПЧ. Кроме того, с ростом частоты (особенно в диапазоне СВЧ) начинают проявляться инерционные свойства ограничителей, что является причиной преобразования паразитной амплитудной модуляции в паразитную фазовую модуляцию, которая создает на выходе ЧД нелинейные искажения полезного сигнала.
Вместе с тем существуют ЧД, мало чувствительные к изменениям амплитуды входного сигнала, так называемые ЧД с внутренним ограничением. Одним из таких ЧД является дробный частотный детектор, или детектор отношений (рис. 7.48). В нем осуществляется фазовое преобразование ЧМ, как и в схеме рис. 7.42, но диоды включены разнополярно. Обычно конденсаторы Сн1, Сн2 и резисторы Rv, R2 выбирают одинаковыми, * а постоянную времени С„ (Ri 4 R-z) выбирают настолько большой, чтобы детекторы на диодах Ди Д2 проявляли инерционные свойства для самых низ-
ких модулирующих частот ПАМ. В этом случае сумма продетектирован-ных напряжений £/_, 1 U_., да да const, т. е. практически постоянна при изменении амплитуды входного напряжения.
Из рис. 7.48 непосредственно следует соотношение 0_аЫх V— - 4- t/_,)/2 = (U_t- U_2)/2, т. е. формируется детекторная характеристика, аналогичная характеристике ЧД на связанных контурах, только с крутизной, в 2 раза меньшей при прочих равных условиях.
Малую чувствительность дробного детектора к ПАМ можно пояснить так. Представим выходное напряжение ЧД в виде
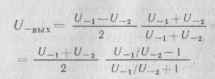
Поскольку U_i + tV_2 да const, а в отношении U_-.IU_2 (отсюда и название детектора — дробный, или детектор отношений) числитель и знаменатель одинаково изменяются при колебаниях амплитуды входного сигнала, выходное напряжение tV_Bblx также будет практически неизменно. Этому результату можно дать следующее физическое толкование.
Так как сумма напряжений (V_i + + <У_2 ="= f/д, cos (->! 4 t/д, cos 62 да да const, то при возрастании амплитуды напряжения на входе напряжения на диодах <Уд,, (Уд2 также должны возрасти, но, поскольку 1)_л 4-4- {/_2 да const, пропорционально уменьшатся cos 0Х и cos в2, что повлечет за собой уменьшение входного сопротивления диодных детекторов на диодах Д\, Д2 и, следовательно, увеличение их шунтирующего действия на контуры. Это приводит к тому, что при возрастании входного сигнала напряжения на диодах (Уд, и £/д2 изменяются в значительно меньшей степени.
В дробном детекторе можно достигнуть подавления ПАМ примерно на 40 дБ вблизи переходной частоты ЧД и до 30 дБ в рабочей полосе частот.
В диапазоне СВЧ из-за влияния паразитных параметров диодов подавление ПАМ в дробном детекторе значительно ухудшается. Поэтому для диапазона СВЧ разработаны другие схемы ЧД с внутренним ограничением (рис. 7.49). Этот ЧД относится
к частотным детекторам с фазовым детектированием и его структурная схема соответствует рис. 7.39.
Роль четырехполюсника с коэффициентом передачи К (/to) выполняет резонатор, включенный на отражение в плечо / первого двойного Т-образного моста. Фазовый детектор собран на втором двойном Т-образном мосте. В качестве опорного напряжения для фазового детектора используется исходный ЧМ-сигнал, подаваемый в Н-плечо (плечо 3) второго моста через регулируемые фазовращатель (ф) и аттенюатор (Ат).
Подавление ПАМ можно проследить с помощью векторных диаграмм (рис. 7.50). Представим для простоты, что волна ая имеет только амплитудную модуляцию и состоит из несущей с двумя боковыми частотами (рис. 7.50, а). Учитывая коэффициент отражения от резонатора Г, ** — — /Qo (Д///о)> находим, что вслнг Ь4, а следовательно, и волна at полу чается из волны ая путем подавления в ней несущей /„ и изменения знакг нижней боковой частоты (рис. 7.50.6) Регулируя фазовращатель, можнс
всегда добиться того, чтобы на входе детектора /' верхние боковые частоты волн a'i и аз сложились в фазе, нижние — в противофазе, а на входе детектора 2' — наоборот. Кроме того, с помощью аттенюатора можно подобрать амплитуду волны а.з так, чтобы результирующие напряжения волн Ощ, на детекторах V, 2' были одинаковы и, следовательно, выходное напряжение было равно нулю (рис. 7.50, в, г).
В общем случае, когда входной сигнал имеет как полезную частотную модуляцию, так и паразитную амплитудную модуляцию, можно показать, что результирующие колебания на детекторах, обусловленные ПАМ. имеют одинаковую амплитуду и к ним добавляются составляющие от полезной частотной модуляции. При этом на выходе дифференциального усилителя ДУ-уровни, обусловленные ПАМ, взаимно компенсируются и остается сигнал, который изменяется в соответствии с закономизменения частоты.
Частотные и фазовые детекторы с преобразованием частотной или фазовой модуляции в импульсные виды модуляции. Частотные и фазовые детекторы этого типа не содержат колебательных цепей и поэтому могут быть с успехом реализованы средствами современной микроэлектроники при частоте сигнала до единиц мегагерц. Функциональная схема ЧД подобного типа изображена на рис. 7.51. Там же приведены эпюры напряжений в различных точках схемы.
Входное синусоидальное ЧМ-коле-бание подвергается двустороннему ограничению в ограничителе мгновен-
ных значений О. Полученная квадратная волна напряжения пропускается через дифференцирующую цепь ДЦ. На выходе ДЦ получается последовательность коротких остроконечных импульсов положительной и отрицательной полярности, возникающих в моменты перепадов напряжения входной квадратной волны. Указанная импульсная последовательность подается на вход формирующей цепи ФЦ, где отрицательные импульсы отсеиваются, а положительные ограничиваются по максимуму и превращаются в почти прямоугольные импульсы стандартной амплитуды и длительности. Эти импульсы детектируются в видеоимпульсном (пиковом) детекторе ПД, выходное напряжение которого обратно пропорционально скважности входной импульсной последовательности q = 77т = 1//т, т. е. пропорционально, частоте входного напряжения.
Как следует из описания работы данного ЧД, в нем ЧМ-колебание преобразуется в импульсную последовательность, модулированную по частоте следования импульсов (ЧИМ). Полученная импульсная последовательность сохраняет всю информацию, заложенную в виде частотной модуляции исходного колебания, и эта информация выделяется пиковым детектором, выходное напряжение которого повторяет по форме модулирующую функцию.
В процессе преобразования ЧМ в ЧИМ полностью устраняется зависимость выходного напряжения от амплитуды входного и детектор является чисто частотным.
Остановимся коротко на особенностях работы частотных детекторов при импульсных сигналах. Одна из особенностей состоит в том, что выходное напряжение частотного детектора образуется в этом случае как результат детектирования импульсов, возникающих на контурах избирательной системы, с последующим вычитанием видеоимпульсов в выходной цепи частотного детектора. Широкое применение в системах АПЧ импульсных приемников получили ЧД с амплитудным и фазовым преобразованием частотных отклонений, т. е. ЧД с расстроенными и связанными настроенными контурами.
При непрерывных сигналах увеличение крутизны детекторной характеристики требовало уменьшения затухания контуров. При импульсных сигналах это может снизить крутизну детекторной характеристики из-за плохого использования спектра импульсного сигнала и снижения амплитуды импульсов на входах амплитудных детекторов, входящих в ЧД. Обычно для импульсных ЧД берут значение
Д/чд = (1.5-Н 3)/ти. (7.78)
Для ЧД со связанными контурами должно быть выполнено условие Л/чд С /о- В противном случае приходится чрезмерно увеличивать коэффициент связи между контурами, что не позволяет получить симметричную детекторную характеристику. Симметрия детекторной характеристики при импульсных сигналах необходима, так как выходной эффект зависит от различия площадей ее положительной и отрицательной полуволн.
Частотные детекторы с расстроенными контурами могут обеспечить большую полосу А/чд при той же центральной частоте /0, чем ЧД со связанными контурами. Этим объясняется их преимущественное использование в широкополосных системах АПЧ.
Снижению затуханий контуров, входящих в состав ЧД, препятствует

также возможность появления побочных переходов через нуль детекторной характеристики. Дело в том, что при воздействии на избирательную систему импульсов с частотой заполнения, отличающейся от резонансной частоты, процесс установления огибающей напряжении имеет колебательный характер. Колебания огибающей обусловлены биениями процессов, происходящих с частотой входного воздействия, и свободных колебаний, происходящих с собственной частотой системы (резонансной час тотой).
Применительно к частотному де тектору с расстроенными контурамк процесс образования побочных нуле? детекторной характеристики иллюстрируется рис. 7.52. На рис. 7.52, с представлены зависимости амплитуд напряжений на контурах частотной: детектора от обобщенной расстрой ки центральной частоты ЧД и часто ты заполнения импульсного сигнал, при некоторой фиксированной дли тельности импульса т„. Такук же форму имеют и зависимо
СТИ LL,(£)|tll~const, U.-i(l)lt„-coibl
Детекторная характеристик*
(рис. 7.52, б) описывается выражение:*.
*М£) |т„= const =U-i(t)U„ со,„. -
Как видно, на ней образуются до полнительные переходы через нул1 при некоторых значениях расстройки
В системах АПЧ подобные «ложные» нули детекторной характеристики или вообще должны отсутствовать, или отстоять достаточно далеко от центральной частоты /„ (I = 0). Условием этого является выполнение неравенства
![]() (7.80)
(7.80)
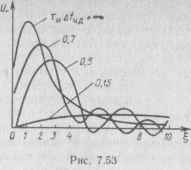
Отсюда можно определить минимальное затухание контуров при заданных /0 и ти. Семейство детекторных характеристик при различных значе-
ниях параметра тиД/чд приведено на рис. 7.53. Характерным является снижение крутизны детекторной характеристики при уменьшении параметра т„Д/чд и появление побочных нулей. Как указывалось, при выборе Д/чд -- (1,5-=-3)/ти эти эффекты проявляются незначительно.
При импульсных входных сигналах выходное напряжение ЧД может быть постоянным или импульсным. Это зависит от постоянных времени нагрузочных цепей амплитудных детекторов. Амплитудные детекторы могут быть пиковыми (RC > Т, где Т период повторения импульсов) или импульсными.
При импульсном выходе требуется равенство амплитуд видеоимпульсов (/_], и_2 и одинаковость их форм при воздействии радиоимпульсов с частотой заполнения, равной переходной частоте ЧД. В противном случае на выходе ЧД не будет точной компенсации разнополярных видеоимпульсов на переходной частоте.
