Простые:

1. ф-ия следования (f(x)=x+1)

2. семейство ф-ий тождества

Iⁿ_m (x₁,x₂,…,x_m,…,x_n)=x_m

3. константа, функция следования, семейство функций тождества

4. Sⁿ_m(h,g₁,g₂,…,g_m)=h(g₁(x₁…x_n),g₂(x₁..x_n),…)

5.  Оператор примитивной рекурсии сопоставляет функциям f от n переменных и g от n + 2 переменных функцию h от n + 1 переменных такую, что для любых натуральных чисел x₁, .. .., x_n, y h(x₁, .., x_n ,0) @ f(x₁, .., x_n) h(x₁, .., x_n, y + 1) @ g(x₁, .., x_n, y, h(x₁, .., x_n, y )).

6. Проверка принадлежности к базису

Проверка по оператору суперпозиции

Проверка по оператору примитивной рекурсии

7. F(x1,…,xn,0)=g(x1,…xn) – фиксируем последний аргумент и смотрим

F(x1,…,xn,y+1)=h(x1,…xn,y, F(x1,…,xn,y-1)) – правило, как подсчитать следующее значение функции

F(x1,…,xn,y)=Rn(g,h)

8. M_y=(f(x₁,…,x_i-1,y,x_i+1,..,x_n))=x_i

9. Ф-ия называется частично-рекурсивной, если она может быть построена из функций 0,f',I путем применения конечного числа операторов примитивной рекурсии, суперпозиции и минимизации

10. Частично-рекурсивная функция называется общерекурсивной, если она всюду определена

11. Смежные слова в ассоциативном исчислении

Два слова P1 и P2 называются смежными в ассоциативном исчислении, если одно из них может быть преобразовано в другое путем подстановок.

12. Дедуктивная цепочка в ассоциативном исчислении

Последовательность слов P1, P2,…, M называется дедуктивной цепочкой от слова P к слову M, если каждое из 2-х рядом стоящих слов смежное с соседним.

13. Эквивалентные слова в ассоциативном исчислении

Слова P и M называются эквивалентными, если существует дедуктивная цепочка от P к M и обратно.

14. Суперпозиция нормальных алгоритмов

При суперпозиции двух алгоритмов А и В выходное слово алгоритма А рассматривается как входное слово алгоритма В. Результат суперпозиции можно представить в виде C(p)=B(A(p)).

15. Объединение нормальных алгоритмов

Объединением алгоритмов А и В в одном и том же алфавите Х называют алгоритм С в том же алфавите, преобразующий любое слово Р, содержащееся в пересечении областей определения алгоритмов А и В, в записанные рядом слова А(р) и В(р). На всех остальных словах этот алгоритм считается неопределенным.

16. Разветвление нормальных алгоритмов

Разветвление алгоритмов представляет собой композицию алгоритмов А, В и С. Обозначая результат этой композиции D, будем считать, что область определения D совпадает с пересечением областей определения всех трех алгоритмов А, В, С, а для любого слова р из этого пересечения

17. Итерация нормальных алгоритмов

Повторение(итерация) представляет собой композицию двух алгоритмов А и В с результатом С.

18. Логика

Это наука, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других высказываний.

19. Цель математической логики

Свести логические заключения к формальным действиям над символами, не затрагивая содержание утверждения (высказывания)

20. Высказывание

Это предположение, относительно которого можно сказать истинно оно или ложно в настоящее время

21) Перечислите основные логические связки (операции)

Конъюнкция И

Дизъюнкция ИЛИ

Инверсия НЕ

Импликация ЕСЛИ – ТО

Неравнозначность ЛИБО – ЛИБО

Эквивалентность

22) Таблица истинности дизъюнкции

A	B	A или B
0	0	0
0	1	1
1	0	1
1	1	1

23) Таблица истинности конъюнкции

A	B	A и B
0	0	0
0	1	0
1	0	0
1	1	1

24) Таблица истинности импликации

Ложно, если первое 1, а второе 0

A	B	A -> B
0	0	1
0	1	1
1	0	0
1	1	1

25) Таблица истинности эквивалентности

Если одинаковые, то истинно

A	B	A <-> B
0	0	1
0	1	0
1	0	0
1	1	1

26) Таблица истинности неравнозначности

Если есть одна 1, то истинно

A	B	A B
0	0	0
0	1	1
1	0	1
1	1	0

27) Порядок выполнения логических операций

Круглые скобки

При отсутствии:

• Отрицание

• &

• Дизъюнкция

• Все остальное слева направо

28) Понятие алгебры

Алгебра логики – наука, рассматривающая логические формулы как алгебраические выражения, которые можно преобразовать по определенным правилам.

29) Носитель алгебры

Множество M с заданной совокупностью операций называют системой алгебры.

O = {M, f1, f2, …, fm}

тут M – носитель алгебры, а O – сигнатура алгебры.

30) типы алгебры

Группы, кольца, поля и решетки

31)сигнатура алгебры

O = {M, f1, f2, …, fm}

32) Подалгебра

Подалгебра — подмножество алгебры над кольцом (алгебраической системы), замкнутое относительно всех операций этой алгебры, и само являющееся алгеброй. Другими словами, если результат бинарной операции над множеством А, не выходит за пределы этого множества.

33) Ассоциативная бинарная операция

Ассоциативная операция — это бинарная операция  , обладающая ассоциативностью  (лат associatio — соединение), или сочетательностью:

 для любых элементов  .

34) Коммутативная бинарная операция

Коммутативная операция — это бинарная операция  , обладающая коммутативностью (от позднелат commutativus — «меняющийся»), то есть переместительностью

 для любых элементов  .

35) Бинарная операция, дистрибутивная слева и справа

свойство согласованности двух бинарных операций, определённых на одном и том же множестве.

Говорят, что две бинарные операции + и × удовлетворяют свойству дистрибутивности, если для любых трех элементов  :

 — дистрибутивность слева;

 — дистрибутивность справа.

36) Логическая переменная

Переменная, принимающая значения 0 или 1, т.е истина или ложь

37) Логическая функция

Это функция вида f(x1, x2, … , xn ), которая принимает логические значения, заданные логическими переменными.

38) Булева алгебра

Алгебра А вида

А = {B, f1, f2,…,fn} называется булевой, если B={0,1}, а f – это логические функции.

39) Фиктивная переменная в логической функции

-Переменная, которая не является существенной для булевой функции, называется фиктивной переменной.

40) Логические функции одной переменной

		Значения переменной   х	0	1
	Название функции	Обозначение функции	Значения  функции
f1	Тождественный нуль	0	0	0
f2	Тождественная	х	0	1
f3	Отрицание		1	0
f4	Тождественная единица	1	1	1

41) Формула

Совокупность переменных и применимых к ним операций

42 Глубина формулы

43 Эквивалентные формулы

2 формулы, представляющие одну функцию, эквивалентны

44 Способы доказательства равносильности формул

Сравнить таблицы истинности

45 Формула разложения функции от n переменных по m переменным

F(x1, xm, xm+1, … xn)=V

46 Совершенная дизъюнктивная нормальная форма

СДНФ - это такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке. 

47 Алгоритм построения СДНФ

Для построения СДНФ из таблицы истинности выбираются функции f=1. Для каждого единичного набора записывается элементарная конъюнкция, в которую переменная входит без инверсий, если в наборе она равна 1, иначе с инверсией.

48 Совершенная конъюнктивная нормальная форма

СКНФ – это такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.

49 Алгоритм построения СКНФ

Для построения СДНФ из таблицы истинности выбираются функции f=0. Для каждого нулевого набора записывается элементарная дизъюнкция, в которую переменная входит без инверсий, если в наборе она равна 0, иначе с инверсией.

50 Ассоциативность логических операций

• Ассоциативность

X & Y & Z=X&(Y&Z)=(X&Y)&Z

X или Y или Z=X или (Y или Z)

51 Коммутативность логических операций

• Коммутативность

X&Y=Y&X

X или Y=Y или X

52 Дистрибутивность логических операций

• Дистрибутивность

X&(Y или Z)=X&Y или X&Z

(Y или Z)&X=Y&X или Z&X

X или (Y&Z)=(X или Y)&(X или Z)

53 Законы идемпотентности (тавтологии)

• Идемпотентность

X&X=X

X или X=X

54 Законы универсального и нулевого множества

• Законы универсальных множеств

X&1=X

X или 1=1

• Законы нулевого множества

X&0=0

X или 0=X

55 Правила (законы) де Моргана

Не(X&Y)=неX или не

Не(X или Y)=неX&неY

56 Закон дополнительности

• Не 0=1 не 1=0

57 Элементарная дизъюнкция

Дизъюнкция любого числа переменных из конечного набора из n – переменных называется элементарной, если в нее входит либо переменные, либо их отрицания

Пример: x1&_x2&x3&_x4

58 Элементарная конъюнкция

Конъюнкция любого числа переменных из конечного набора из n – переменных называется элементарной, если в нее входит либо переменные, либо их отрицания.

59 Ранг элементарной дизъюнкции (конъюнкции)

Рангом элементарной дизъюнкции (конъюнкции) называется количество ее операндов, переменных.(Не n!)

60 Конституента нуля

Элементарная дизъюнкция ранга n (r=n) называется конституентой нуля

61 Конституента единицы

Элементарная конъюнкция ранга n (r=n) называется конституентой единицы

62 Соседние элементарные дизъюнкции (конъюнкции)

Элементарные дизъюнкции (конъюнкции) называются соседними, если в них участвуют одни и те же переменные, и они отличаются только инверсией одной переменной.

63 Правило склеивания

Дизъюнкцию двух соседних конъюнкций можно заменить одной элементарной конъюнкцией, которая является общей частью.

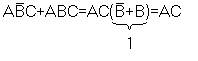
Аналогично с конъюнкцией

64 Правило поглощения

Дизъюнкцию двух элементарных конъюнкций, одна из которых является частью другой, можно заменить одной элементарной конъюнкцией, имеющее меньшее количество операндов.

65 Правило развертывания

Это правило противоположно правилу склеивания и позволяет получить из элементарной конъюнкции дизъюнкцию элементарных конъюнкций большего ранга.

66 Полная система в алгебре логики

A = {f1, f2, … , fn} называется полной системой, если любую другую функцию алгебры-логики можно выразить через A

67 Минимальный базис

Базис является минимальным, если удаление хотя бы одной fi делает систему неполной

68 Перечислите примеры полных систем

Системы И, ИЛИ, НЕ