3.2 Локализация корней

В большинстве случаев отделение корней можно произвести графически, однако в более сложных случаях для исследования вопроса о наличии (и количестве) корней уравнения на заданном отрезке целесообразнее воспользоваться инструментальным пакетом или составить программу для компьютера на языке программирования.

При решении задачи о локализации корней применяют следующие положения:

1. Если непрерывная на отрезке [a; b] функция F(x) принимает на его концах значения разных знаков (т.е. F(a)∙F(b) < 0), то уравнение F(x)= 0 имеет на этом отрезке по меньшей мере один корень.

2. Если функция F(x) к тому же еще и монотонна, то корень на отрезке [a; b] единственный.

Локализация корней с помощью Excel путем табулирования:

1.Выбирают отрезок, на котором будет проводиться отделение корней, например [-10; 10] и шаг табулирования h, например h = 0,1.

2. Колонка А – значения х. В клетку А1 вводят левое значение интервала: –10 В клетку А2 вводят формулу для табуляции = А1 + 0,1. Копируют операцию до значения 10.

3. Колонка В – значения функции. В клетку В1 вводят исходную функцию (в формуле х заменяют на А1), получают ее значение. Копируют операцию для всех значений х.

4. Строят график: выделяют все полученные значения, открывают диаграмму в меню вставка, используют точечную диаграмму.

5. Количество корней удобно определить по графику: количество пересечений с осью х. Отрезками, в которых находятся корни будут те значения х, при которых значение функции меняет свой знак.

Пример:

Для функции локализация корней на интервале (–1; 1) путем табулирования с помощью Excel показана на рис. 3.2

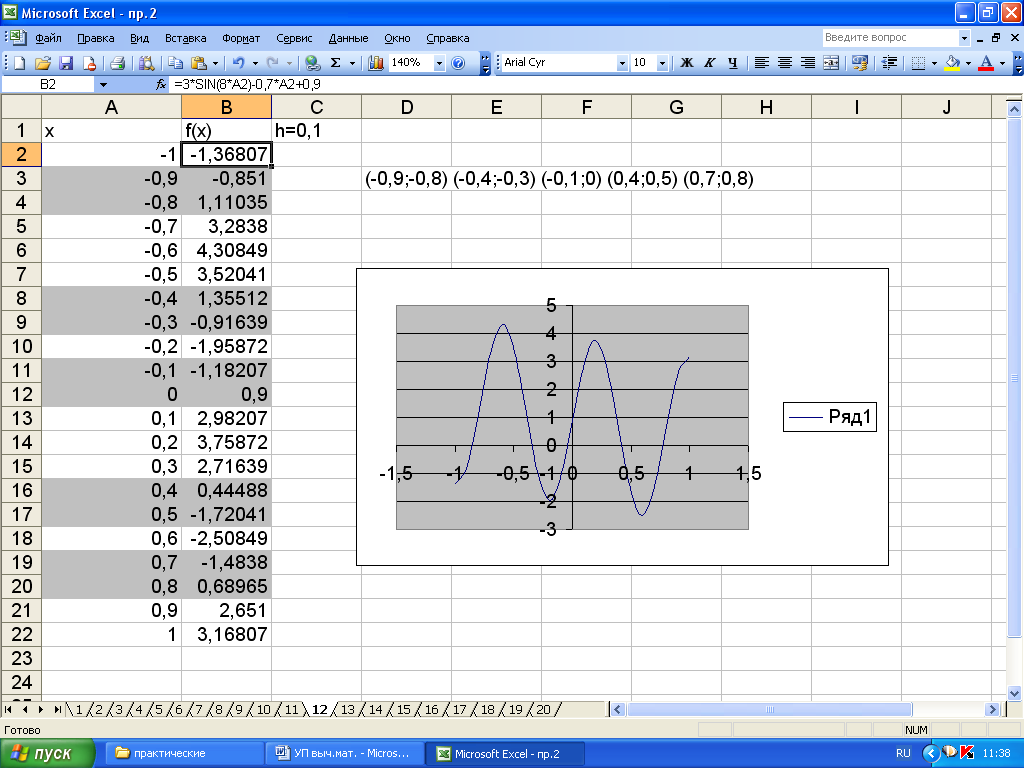
Рисунок 3.2. Локализация корней нелинейного уравнения в MS Excel

3.3 Метод деления отрезка пополам (метод бисекции, метод дихотомии)

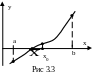На этапе локализации было установлено, что на отрезке [a, b] функция y=f(x) меняет знак, т.е. имеем f(a)·f(b)<0 и имеется всего один корень (рис.3.2). Предположим, что функция непрерывна, тогда внутри отрезка имеется точка с, где y=f(c)=0, a< c <b.

В качестве начального приближения выбирается точка , лежащая посередине отрезка [a,b], которая делит этот отрезок на два отрезка равной длины и вычисляется значение функции в этой точке y₀=f(x₀). Далее рассматривается один из двух отрезков, на концах которого функция имеет разные знаки, т.к. корень может находиться только на этом отрезке. Этот отрезок в два раза меньше первоначального. В качестве первой итерации принимают середину этого нового отрезка и т.д. Таким образом, после n итераций отрезок [a,b] уменьшился в 2ⁿ раз, отсюда имеем . Следовательно, метод бисекции сходится со скоростью геометрической прогрессии, знаменатель которой . По сравнению с другими методами он обладает более медленной сходимостью, но зато очень надежен. Для его применения необходимо чтобы функция была непрерывна и обязательно меняла знак на концах отрезка.

Условие непрерывности обязательно, т.к. функция может менять знак в окрестности некоторой точки и одновременно стремится к , т.е. функция имеет особенность внутри отрезка [a,b]. Естественно метод не годится для поиска кратных корней, когда функция y=f(x) не меняют знак.