Примеры выполнения заданий работы

Задание 1. Для функции, заданной таблицей узловых значений, составить формулу интерполяционного многочлена Лагранжа, вычислить с его помощью одно значение функции для промежуточного значения аргумента х^*.

х	-1	0	1	2
f(x)	0,5	1	2	4

х^* = 0,3

Решение:

Из таблицы следует, что n = 3 (т.к. в таблице четыре узла).

= =

=

Вычислим значение функции при х^* = 0,3

f(0,3) = = 1,236

Задание 2. Вычислить значение заданной функции f(x) для промежуточного значения аргумента х^* по интерполяционному многочлену Лагранжа с помощью вычислительной таблицы.

х	0,41	1,55	2,67	3,84
f(x)	2,63	3,75	4,87	5,03

х^* = 1,91

Решение:

х = 1,91	х0=0,41	х1=1,55	х2=2,67	х3 =3,84	рi	yi	yi / pi
х0=0,41	1,50	– 1,14	– 2,26	– 3,43	– 13,26	2,63	– 0,198
х1=1,55	1,14	0,36	– 1,12	– 2,29	1,05	3,75	3,561
х2=2,67	2,26	1,12	– 0,76	– 1,17	2,25	4,87	2,163
х3 =3,84	3,43	2,29	1,17	– 1,93	– 17,74	5,03	– 0,284
							5,242

f(1,91) = 5,242∙1,50∙0,36∙(– 0,76)∙(– 1,93) = 4,15

Контрольные вопросы

1. Что из себя представляет аппроксимация функций?

2. В чем отличие экстраполяции от интерполяции?

2 Каким образом составляется многочлен Лагранжа?

3 В каких случаях используется вычислительная таблица Лагранжа?

4 Каким образом может быть оценена точность получения значения функции по многочлену Лагранжа?

5. Как используются программные средства для аппроксимации функций?

5.3 Интерполяционные формулы Ньютона

Часто интерполирование ведется для функций, заданных таб­лицами с равноотстоящими значениями аргумента. В этом случае шаг таблицы h = x_i+i – x_i (i=0, 1, 2, ...) является величиной по­стоянной. Для таких таблиц применяют интерполяци­онные формулы Ньютона.

Конечные разности

Пусть задана функция y = f (x) и Δx = h – фиксированный шаг аргумента, тогда приращением или первой конечной разностью функции y называется выражение

Δy = Δf (x) = f (x + Δx) − f (x) .

n-й конечной разностью функции y будет Δⁿ y = Δ(Δ^n–1 y) (5.3)

Например, вторая конечная разность имеет вид

Δ² y = Δ(Δy) = Δ( f (x + Δx) − f (x)) = f (x + 2Δx) − 2 f (x + Δx) + f (x) .

По заданной таблице функ­ции можно составить таблицу конечных разностей (табл. 5.2)

Таблица 5.2

х0	y0
		Δy0
x1	y1		Δ2y0
		Δy1		…
x3	y3
		…			Δn y0
…	…		…
		…		…
xn-1	yn-1		Δ2yn -2
		Δyn -1
xn	yn

Первая интерполяционная формула Ньютона

Пусть заданы узлы интерполяции x₀, x₁,…, x_n причем расстояния между узлами одинаковы: h = x_i+i – x_i - const, h – шаг интерполяции. Требуется найти для функции y = f (x) такой многочлен P_n (x) , что P_n (x) = y_i и Δ^k P(x₀) = Δ^k y₀ , для k, i = 0, 1, 2,…, K,…, n .

P_n (x) будем искать в виде

P_n (x) = a₀+a₁(x–x₀)+ a₂(x–x₀)(x–x₁)+…+ a_n(x–x₀) (x–x₁)·…· (x–x _n–1).

Используя понятие обобщенной степени числа, запишем его как

P_n (x) = a₀+a₁(x–x₀)^[1] + a₂(x–x₀)^[2] +…+ a_n(x–x₀)^[n].

Для определения коэффициентов a_i , i = 0, 1, 2, … , n вычислим k-е конечные разности полинома P_n (x) в точке x₀, k = 0, 1, 2, … , n и приравняем их значения k-м конечным разностям самой функции f (x₀) :

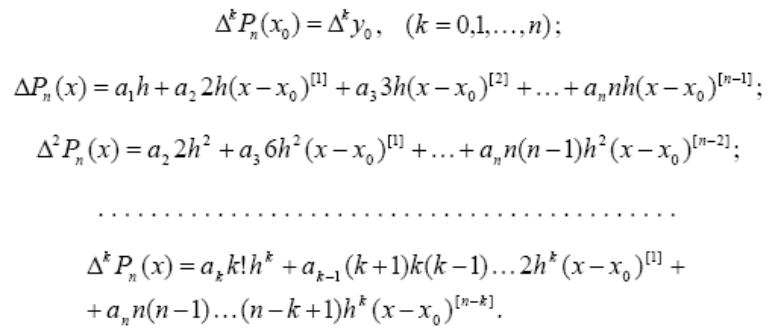
Так как при x = x₀ все члены в Δⁱ P_n (x), кроме первого, равны нулю, получаем:

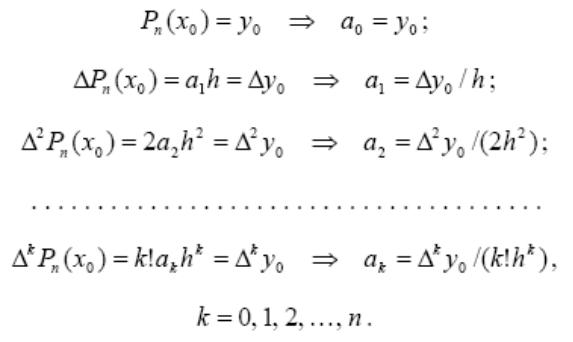
Подставляя найденные значения a _k в полином P_n (x), имеем

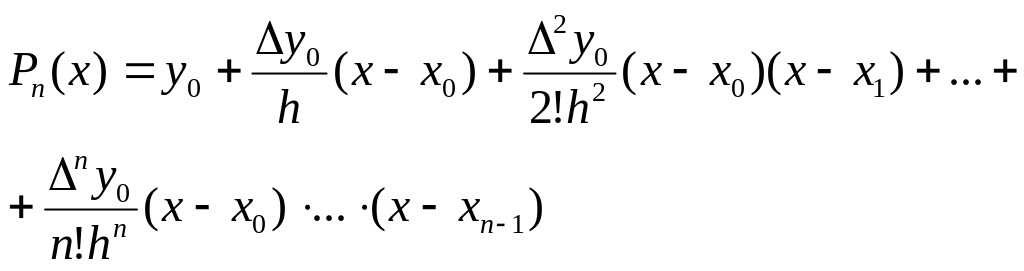(5.4)

Формула называется первой интерполяционной формулой Ньютона.

Часто эта формула записывается в несколько ином виде.

Введя переменную t= (x–x₀) / h, первая формула Ньютона примет вид:

(5.5)

Первая интерполяционная формула Ньютона применяется для интерполирова­ния в начале отрезка интерполяции, для значений t в интервале (0, 1). Первую интерполяционную формулу Ньютона называют по этой причине формулой для интерполирования вперед.

Когда значение аргумента находится ближе к концу отрезка интерполяции, применяется формула для интерполирования на­зад – вторая интерполяционная формула Ньютона

Вторая интерполяционная формула Ньютона

Вторая интерполяционная формула Ньютона ищется в виде:

P_n (x) = a₀+a₁(x–x _n)+ a₂(x–x _n)(x–x _n–1)+…+ a_n(x–x _n) ·…· (x–x₁).

Таким образом вторая интерполяционная формула Ньютона имеет вид:

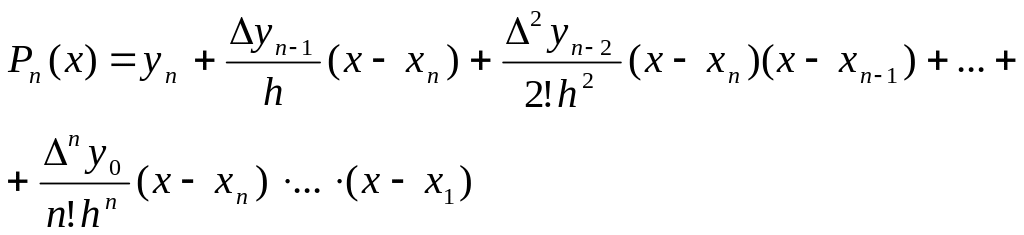(5.6)

При замене t= (x–x _n) / h, вторая формула Ньютона примет вид:

(5.7)

Оценка погрешности для первой формулы Ньютона может производится по формуле: (5.8),

для второй формулы Ньютона:

(5.9)

Предполагая, что Δⁿ⁺¹ y почти постоянно для функции y = f (x) и h достаточ-

но мало для формул Ньютона можно получить:

(5.10)

(5.11)