Контрольные вопросы.

1. Каков алгоритм решения уравнений методом касательных?

2. Каков алгоритм решения уравнений методом хорд?

3. По каким причинам методы хорд и касательных предпочтительнее метода простой итерации?

4. Каким образом математические программные средства используются для решения нелинейных уравнений?

§4. Методы решения систем уравнений

4.1 Система линейных уравнений

Системой n линейных алгебраических уравнений с n неизвестными называется система имеющая вид:

, j=1,2,...,n. (4.1)

Методы решения такой системы можно разделить на 2 класса:

1. прямые методы: метод определителей (Крамера), матричный метод(с помощью обратной матрицы) и метод Гаусса;

2. итерационные методы – методы основанные на применении принципа сжимающихся отображений.

4.1.1 Прямые методы решения систем линейных уравнений

В матричном виде система линейных алгебраических уравнений записывается следующим образом:

, (4.2)

где A - квадратная матрица, а и - матрицы - столбцы:

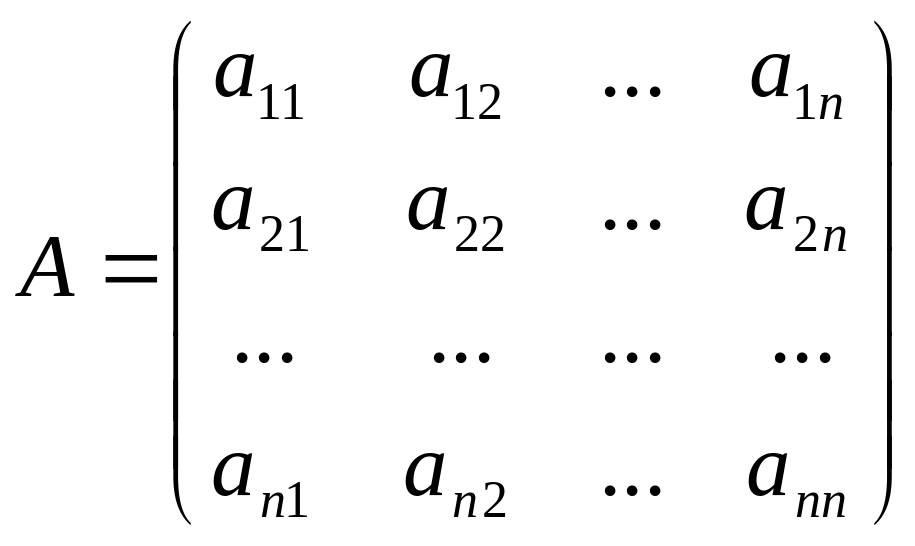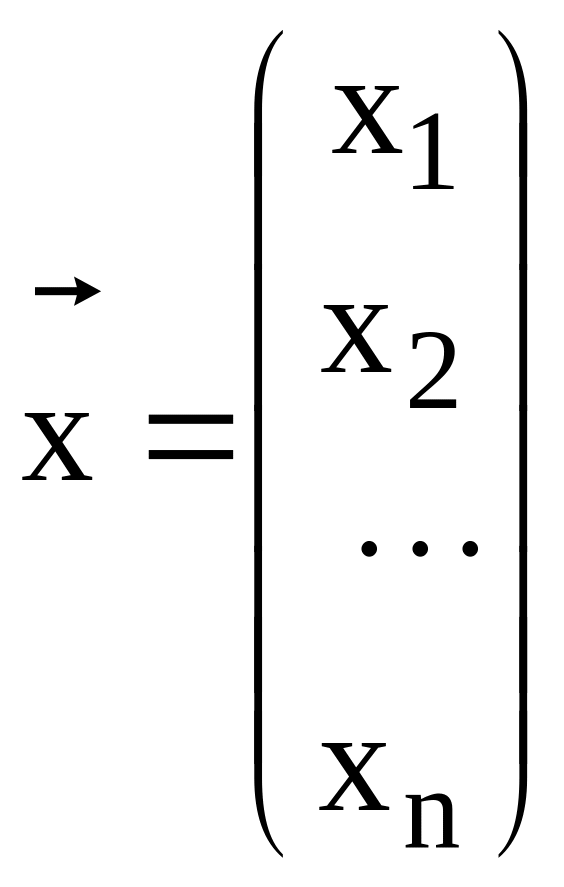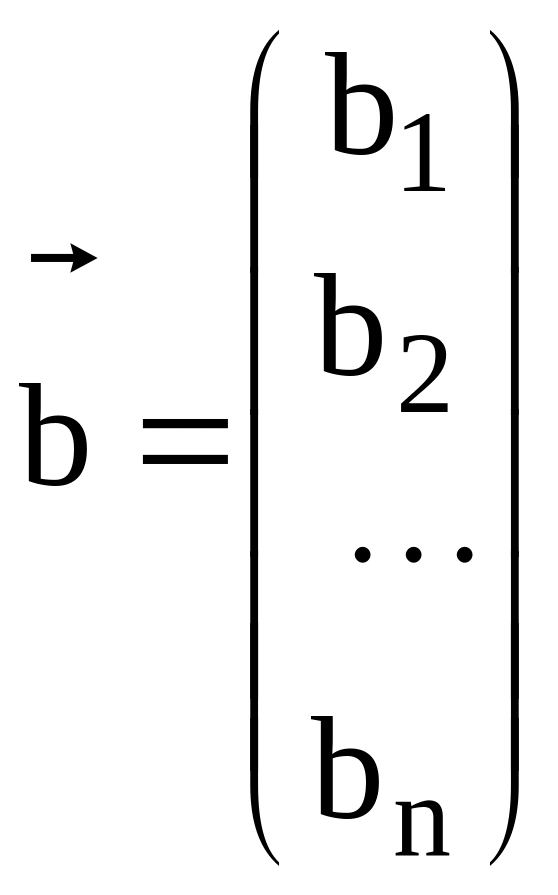, , . (4.3)

Признак вектора у величин и говорит о том, что мы имеем дело с величинами, определяемыми наборами элементов x₁,...,x_n и b₁,...b_n. Причем каждому единственному набору x₁,...,x_n сопоставляется единственная величина , набору b₁,...b_n - величина . Операции сложения и вычитания величин и осуществляются по правилу сложения и вычитания векторов, т.е. по правилу параллелограмма.

Уравнение (4.2) можно интерпретировать следующим образом. Если величины и являются элементами векторного пространства Rⁿ (n - мерного пространства вещественных чисел), то матрица А является линейным оператором A в этом пространстве, который преобразует вектор пространства Rⁿ в вектор того же пространства: . Действительно на основании правила умножения матрицы на некоторую величину и правила сложения двух матриц можем записать: , , т.е. оператор A - является линейным оператором в пространстве Rⁿ.

Определителем (детерминантом) матрицы А порядка n (системы из n линейных алгебраических уравнений) называется число _n (Det A) равное:

, (4.4)

где p - порядковый номер одной из перестановок чисел 1,2,...n; P=n! - максимальное количество таких перестановок; значения индексов ..., соответствуют перестановке с номером p, k - число инверсий в данной перестановке.

Если в перестановке значение предыдущего индекса (например, индекса ) больше значения одного из последующих индексов (например, индекса ), то говорят, что в данной паре индексов (паре  и ) имеется инверсия. Поэтому, если в перестановке имеется k таких пар, то данная перестановка имеет k инверсий.

Существует другое определение детерминанта матрицы. Детерминантом (определителем) матрицы А порядка n называется число равное:

(4.5)

где ¹ⁱ_n-1 - определитель матрицы A_1i порядка (n-1), которая образована исключением из матрицы А первой строки и i - го столбца. Определитель ¹ⁱ_n-1 называется минором, а величина (-1)^i-1a_1i называется алгебраическим дополнением. Определитель матрицы, состоящей всего из одного элемента, например, a_ij равен самому этому элементу ₁=a_ij.

Формулу (4.5) часто называют правилом вычисления определителя по первому столбцу. Определения (4.4) и (4.5) эквивалентны. Из одного следует другое и наоборот.

Необходимым и достаточным условием существования единственного решения системы линейных алгебраических уравнений является условие _n0. В случае равенства нулю определителя матрица является вырожденной, при этом система (4.1) либо не имеет решение, либо имеет их бесчисленное множество.

Правило Крамера. Решение системы (4.1) представляется в виде:

(4.6)

где _jn - определитель порядка n, образованный из матрицы A заменой элементов j-го столбца на элементы столбца свободных членов .

Этот метод используется при решении уравнений малого порядка. Для решения системы из n уравнений необходимо найти значения (n+1) определителя, а для вычисления определителя необходимо вычислить n! слагаемых каждое из которых состоит из n произведений. Поэтому количество операций N равно: N(n+1)(n!)n(n+2)!.

Таким образом, количество операций катастрофически нарастает с ростом n. Например, для n=10 требуется N=12! операций, откуда N10⁸.

Метод Гаусса. Этот метод состоит из двух этапов: прямого хода и обратного хода. На первом этапе (прямой ход) матрица приводится к треугольному виду. Рассмотрим систему:

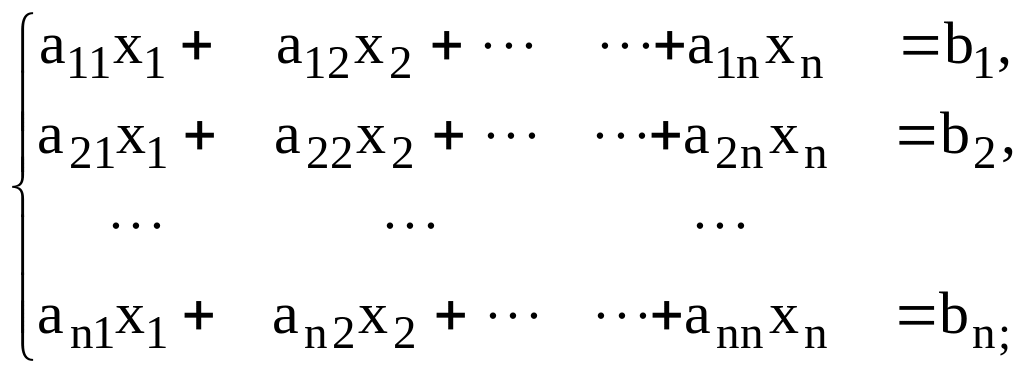(4.7)

Предположим, что элемент первой строки, расположенный на главной диагонали не равен нулю: a₁₁0. Исключим x₁ из второго уравнения. Для этого умножим первое уравнение на s₂₁= – а₂₁/а₁₁ и сложим со вторым. В итоге получим:

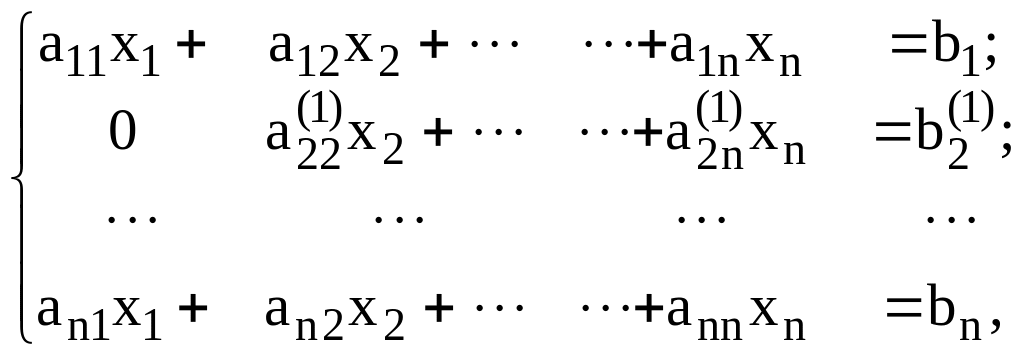(4.8)

где элементы второй строки вычисляются по формуле

Естественно решение системы не изменится.

Исключим x₁ из третьего уравнения. Для этого умножим первое на s₃₁= – a₃₁/a₁₁ и сложим с третьим. В результате в третьей строке получим элементы

,

при этом элемент первого столбца .

Процедуру исключения проделаем для всех оставшихся уравнений. В результате получим новую систему уравнений, в которой все элементы первого столбца, расположенные ниже главной диагонали равны нулю:

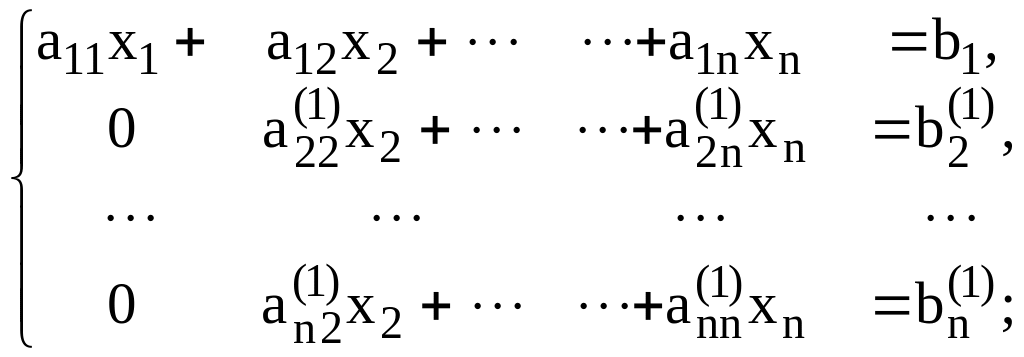(4.9)

при этом новые элементы вычисляются по формулам:

(4.10)

где s_j1= – a_j1/a₁₁.

Аналогично полагая, что элемент, стоящий на главной диагонали во второй строке , исключим все элементы второго столбца уравнения (4.9) стоящие ниже главной диагонали, и так далее до n - го столбца. В результате получим систему уравнений с верхней треугольной матрицей, у которой все элементы ниже главной диагонали равны нулю:

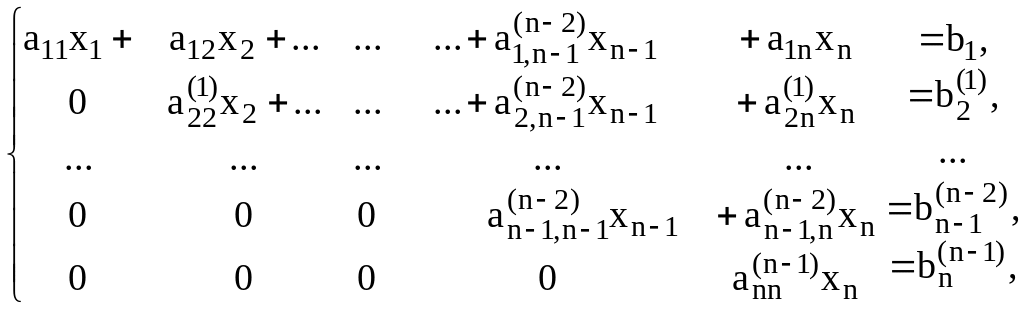(4.11)

где

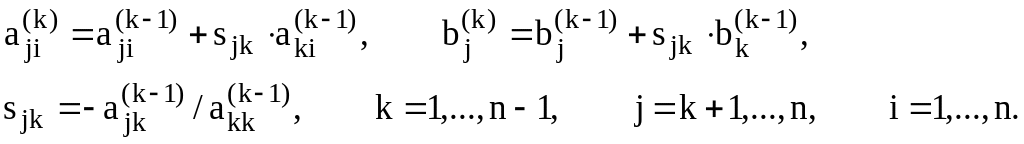(4.12)

Формулы (4.12) являются общим алгоритм исключения j - той строки и k - го столбца метода Гаусса. Они получены из (4.10) (формулы исключения 1 - го столбца) заменой индекс 1 на индекс k.

Обратный ход состоит в вычислении искомых величин. Из последнего уравнения определяется значен6ие и это значение переносится в правую часть уравнения (значение заменяется на значение x_n). Далее подставляем x_n в (n-1) ое уравнение и определяем x_n-1 и т.д. до x₁. Таким образом, полученное решение будет находиться в столбце свободных членов.

Для того, чтобы избежать деления на 0, а также для уменьшения погрешности округления, в столбце выбирается максимальный по модулю элемент и с помощью перестановки строк он делается диагональным. Это называется выбором главного элемента по столбцу. Аналогично можно осуществить выбор главного элемента по строке.

Если выбор главного элемента осуществляется по столбцу или строке , то такие схемы называются схемами частичного выбора, если по всей матрице, то схемой глобального выбора. Обычно используется схема выбора главного элемента по столбцу.

Оценим количество операций. При исключении x₁ из 2 - го уравнения мы делаем (n+1) умножений и (n+1) сложений, т.е. 2(n+1) операций. Следовательно, для исключения из всех строк (таких строк n-1) необходимо выполнить N₁=2(n+1)(n-1)=2(n²-1)2n² операций. На следующем этапе N₂2(n-1)² и т.д. Общее количество операций равно:

NN₁+N₂+...+N_n=2n²+2(n-1)²+...+22n³/3.

Метод Гаусса уже при n=2 имеет преимущество по сравнению с правилом Крамера, не говоря уже о больших n.

Пример. Методом Гаусса решить следующую систему уравнений: . Расчеты проводить с четырьмя знаками после запятой.

; .

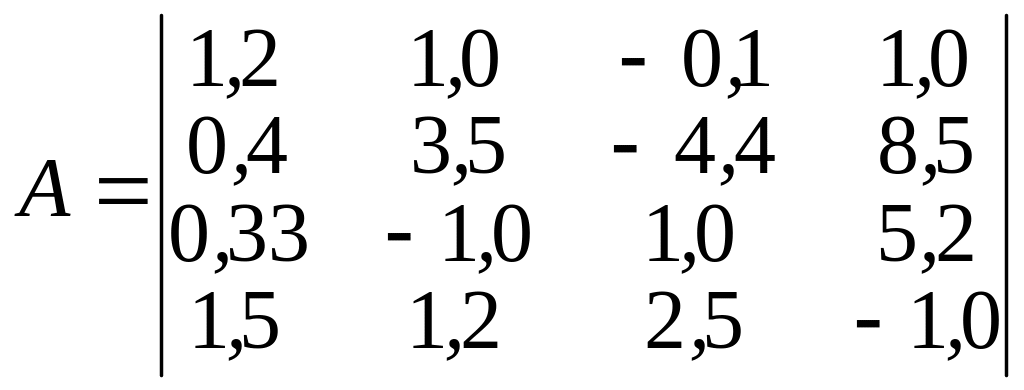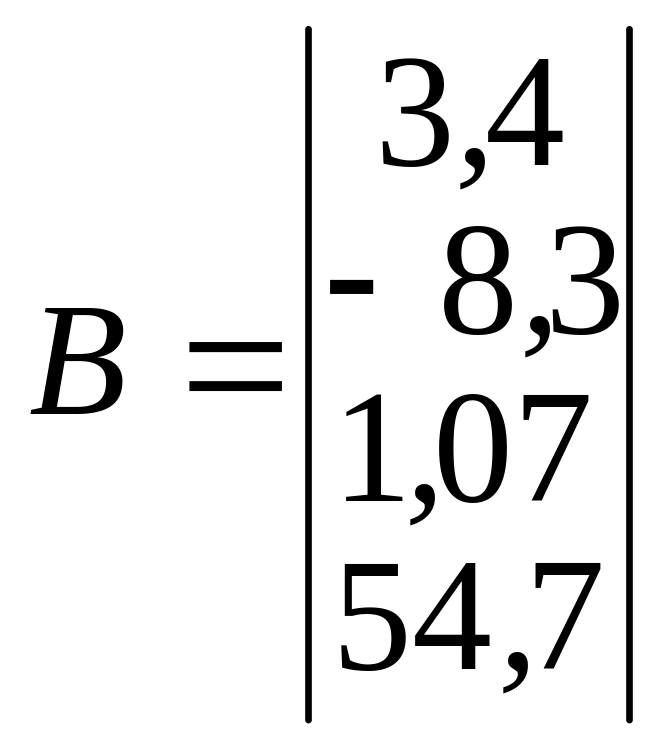Решение.

Записываем систему уравнений:

;

;

;

.

Прямой ход

В первом столбце выбираем максимальный по модулю коэффициент. Это элемент четвертой строки, имеющий значение 1,5. Переставляем первую и четвертую строки местами, делая элемент 1,5 диагональным.:

;

;

;

.

Исключаем неизвестное из всех строк, начиная со второй. Для этого первую строку умножаем на и складываем со второй, умножаем первую строку на и складываем с третьей, умножаем первую строку на и складываем с четвертой. В итоге получаем:

;

;

;

.

Исключаем неизвестное из всех строк, начиная с третьей. Так как максимальный по модулю элемент находится во второй строке, т.е. является диагональным, то строки не переставляем. Умножаем вторую строку на и складываем с третьей, умножаем вторую строку на и складываем с четвертой. Имеем:

;

;

;

.

Исключаем неизвестное х₃. Так как максимальный по модулю элемент находится в четвертой строке, то переставляем третью и четвертую строки местами, чтобы сделать его диагональным:

;

;

;

.

Умножаем третью строку на и складываем с четвертой. Получаем:

;

;

;

.

Так как мы имеем верхнетреугольную матрицу, то прямой ход метода Гаусса завершен.

Обратный ход

Из последнего уравнения определяем х₄, затем из третьего х₃, из второго х₂ и из первого х₁. Получаем:

;

;

;

.

Иногда, преобразования удобнее производить не с уравнениями системы, а с матрицей системы, и вычисления оформлять в виде расчетной таблицы.

Используя метод Гаусса и свойство определителя матрицы, по которому определитель треугольной матрицы равен произведению элементов главной диагонали, можно вычислять определитель произвольной матрицы. Для вычисления определителя некоторой квадратной матрицы, необходимо решить систему уравнений с этой матрицей и произвольной правой частью и определитель будет равен произведению ведущих элементов.

Если матрица сводится не к треугольному, а диагональному виду, то такая модификация метода Гаусса называется методом Жордана-Гаусса. Он требует 2n³ операций и обычно применяется для нахождения обратных матриц.