7.3 Метод Рунге – Кутта

Семейство методов Рунге-Кутты основано на аппроксимации неизвестных аргументов y (t_n) в правых частях дифференциальных уравнений f(t,y).

Рассмотрим идею этих методов на примере алгоритма 2-го порядка.

Для метода Эйлера путем простейшей правосторонней аппроксимации производной имеем: . В это выражение входят значения функции в двух точках. Если взять в правой части дифференциального уравнения y ' = f(x, y) значение f(x, y) в точке с номером i, то придем к методу Эйлера. Однако можно рассудить и иначе: раз для аппроксимации производной взяты две точки, то лучшей аппроксимацией правой части уравнения будет полусумма . Тогда для нахождения y_i+1 получим равенство . Поскольку оно представляет собой уравнение для y_i,, то решать его можно ме­тодом итераций, причем в качестве первого приближения взять то значение y_i+1, которое определяется методом Эйлера. В итоге получим формулы Рунге – Кутта 2-го порядка:

(7.3),

где ,

Чем выше порядок формул Рунге—Кутта, тем более точные значения они дают. На практике соблюдается некоторый компро­мисс между высоким порядком формул и их громоздкостью, с одной стороны, и объемом вычислений по ним для достижения заданной точности, с другой.

Одной из самых по­пулярных является формула 4-го порядка, часто называемая просто, без уточнений, формулой Рунге — Кутта:

(7.4),

где ,

, ,

Погрешность данного метода Рунге – Кутта на шаге пропорциональна пятой степени шага ξ ~ h⁵.

Общий недостаток методов Рунге—Кутта — отсутствие про­стых способов оценки погрешности метода. Погрешность на од­ном шаге оценить сравнительно нетрудно, гораздо труднее оце­нить накопление погрешностей на протяжении многих шагов. Широко используемый на практике для этих методов полуэмпи­рический способ контроля точности — двойной счет.

Задания для самостоятельного решения

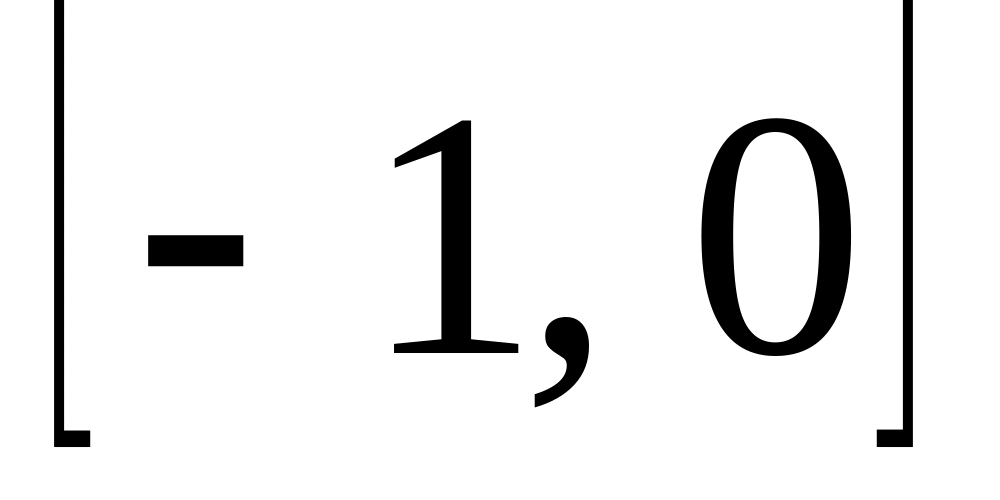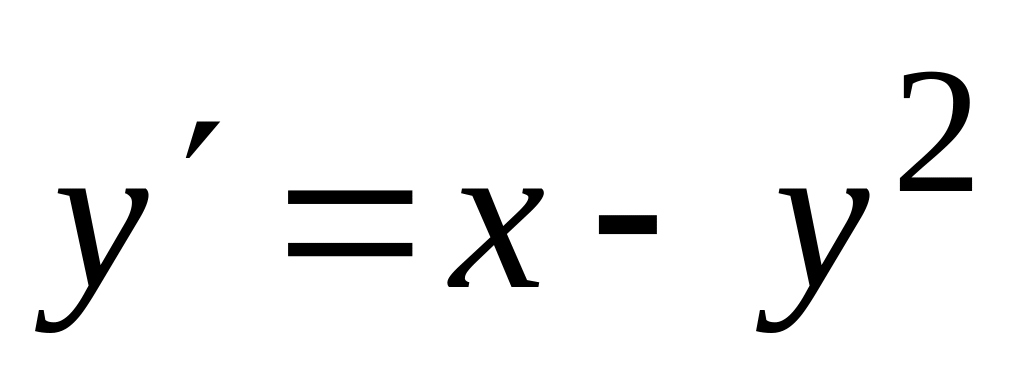1. Используя метод Эйлера, на отрезке с шагом численно решить дифференциальное уравнение при заданном начальном условии .

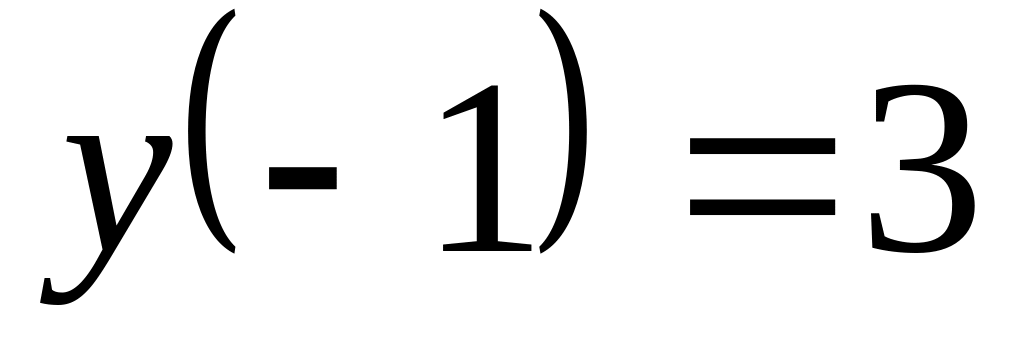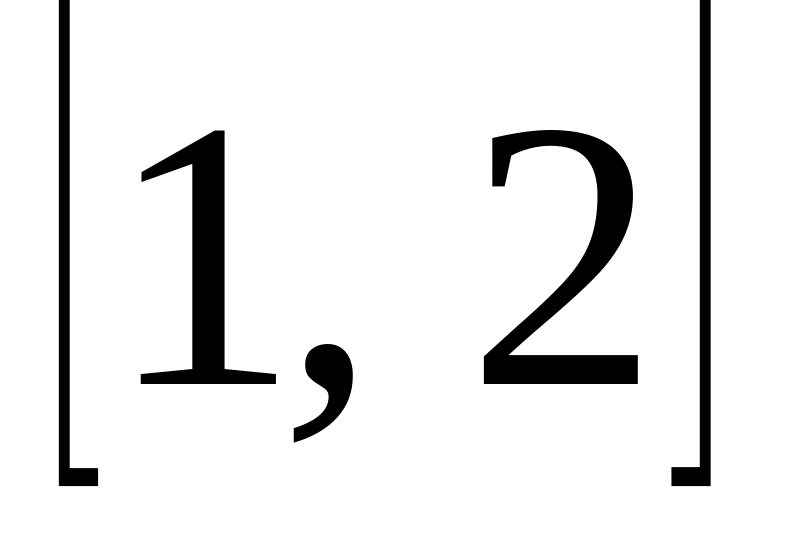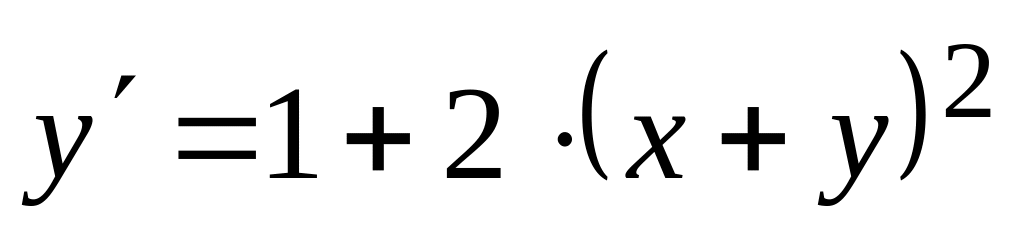2. Используя метод Рунге-Кутта, на отрезке с шагом численно решить дифференциальное уравнение при заданном начальном условии .

3. Используя усовершенствованный метод Эйлера-Коши, на отрезке с шагом численно решить дифференциальное уравнение 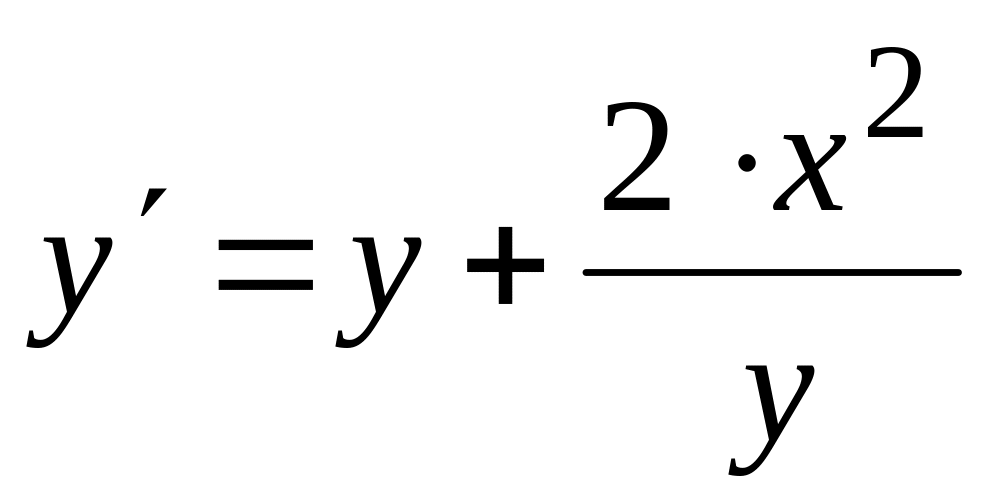при заданном начальном условии .

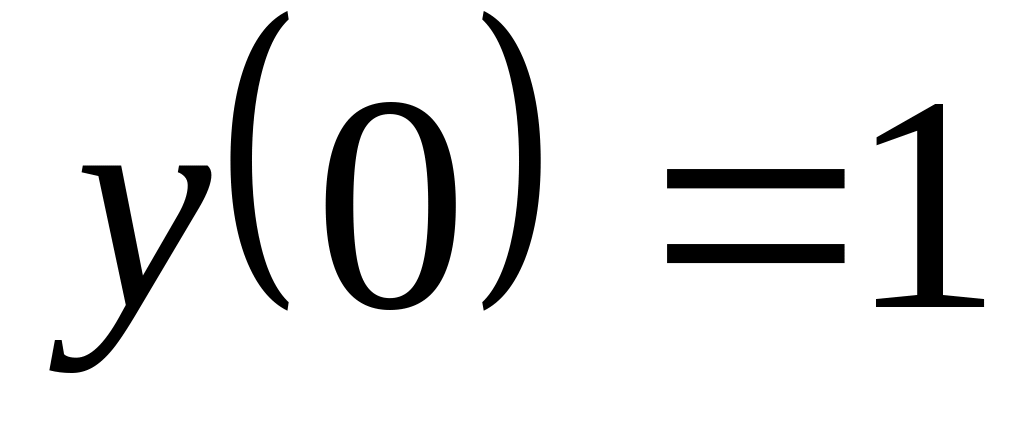4. Используя метод Эйлера-Коши, на отрезк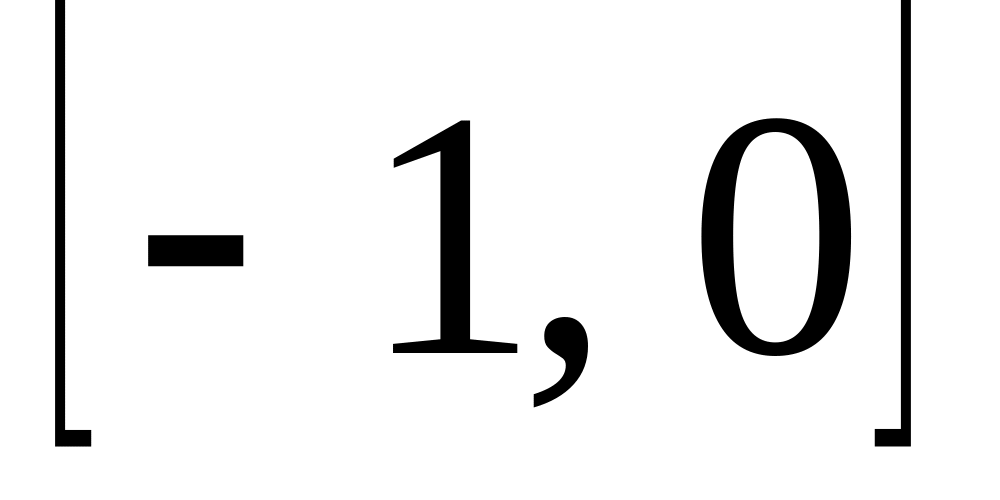е с шагом численно решить дифференциальное уравнение 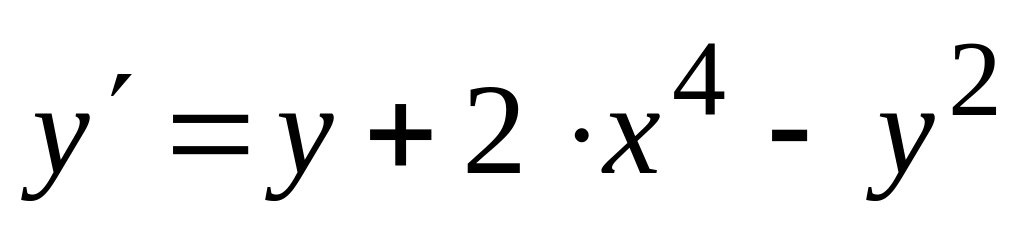при заданном начальном условии y(–1)=1.

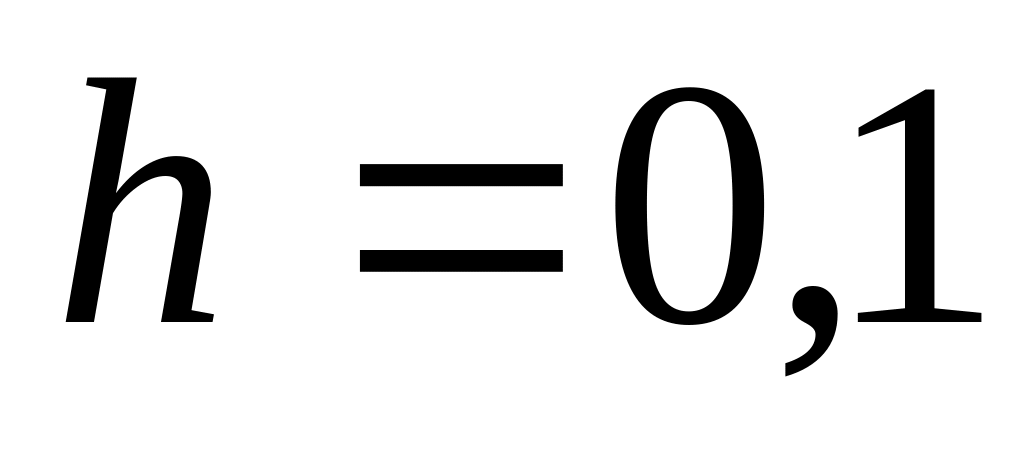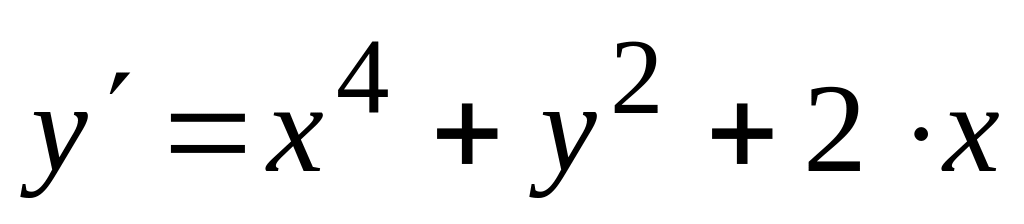5. Используя математические программные средства, на отрезке с шагом численно решить дифференциальное уравнение при заданном начальном условии у (0) = 0.

Практическая работа №9

Тема: «Решение дифференциальных уравнений»

Цели: освоение решения дифференциальных уравнений с помощью метода Эйлера и уточненного метода Эйлера; оценка точности результатов методом двойных вычислений.

Задания.

1. Решить задачу Коши для дифференциального уравнения у' = f(x,у) на отрезке [a; b] при заданном начальном условии у(х₀) = у₀ и шаге интегрирования 2h с помощью метода Эйлера.

2. Произвести те же вычисления с шагом h.

3. Свести результаты вычислений в одну таблицу и сопоставить точность полученных значений функции.

4. Решить задачу Коши для дифференциального уравнения у' = f(x,у) на отрезке [a; b] при заданном начальном условии у(х₀) = у₀ и шаге интегрирования 2h с помощью метода Эйлера - Коши.

Исходные данные:

Вариант 1. f(x; y) = xy³ – x² на отрезке [4; 5] , у(4) = 0,7; h = 0,1

Вариант 2. на отрезке [2,6; 4,6] , у(2,6) = 1,8; h = 0,2

Вариант 3. на отрезке [0; 0,5] , у(0) = 0,3; h = 0,05

Вариант 4. f(x; y) = 4,1x – y² +0,6 на отрезке [0,6; 2,6] , у(0,6) = 3,4; h = 0,2

Вариант 5. на отрезке [2,1; 3,1] , у(2,1) = 2,5; h = 0,1

Вариант 6. f(x; y)= 2,5x+ cos(y + 0,6) на отрезке [1; 3] , у(1) = 1,5; h = 0,2

Вариант 7. на отрезке [0,1; 0,5] , у(0,1) = 1,25; h = 0,05

Вариант 8. на отрезке [-2; -1] , у(-2) = 3; h = 0,1

Вариант 9. f(x; y) = sin(x + y) + 1,5 на отрезке [1,5; 2,5] , у(1,5) = 0,5; h = 0,1 Вариант 10. f(x; y) = e^{2 x} + 0,25y² на отрезке [0; 0,5] , у(0) = 2,6; h = 0,05

Вариант 11. f(x; y) = cos(1,5x – y²) 1,3 на отрезке [-1; 1] , у(-1) = 0,2; h = 0,2

Вариант 12. f(x; y) = x² + xy + y² на отрезке [2; 3] , у(2) = 1,2; h = 0,1

Вариант 13. f(x; y) = cos(1,5y + x)² + 1,4 на отрезке [1; 2] , у(1) = 0,9; h = 0,1

Вариант 14. на отрезке [1,5; 2] , у(1,5) = 2,1; h = 0,05

Вариант 15. на отрезке [3; 5] , у(3) = 1,7; h = 0,2

Вариант 16. f(x; y) = x + 2,5y² + 2 на отрезке [1; 2] , у(1) = 0,9; h = 0,1

Вариант 17. f(x; y) = 2 - sin(x + y)² на отрезке [2; 3] , у(2) = 2,3; h = 0,1

Вариант 18. на отрезке [0; 2] , у(0) = 2,9; h = 0,2

Вариант 19. на отрезке [1,5; 2] , у(1,5) = 1,4; h = 0,05

Вариант 20. f(x; y) = 0,4x² + y² на отрезке [1; 3] , у(1) = 1,8; h = 0,2