Задания для самостоятельного решения

1. Найти точку минимума функции с точностью 0,1, используя метод деления отрезка пополам.

2. Найти точку минимума функции с точностью 0,1, используя метод золотого сечения.

3. Найти точку минимума функции с точностью 0,1, используя метод деления отрезка пополам.

4. Найти точку минимума функции с точностью 0,1, используя оптимально-пассивный поиск.

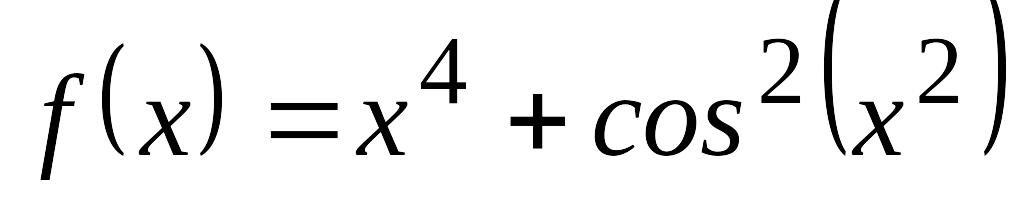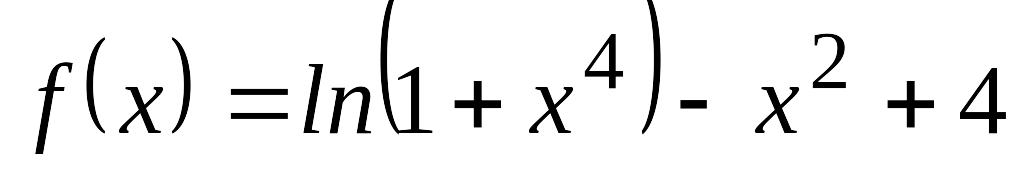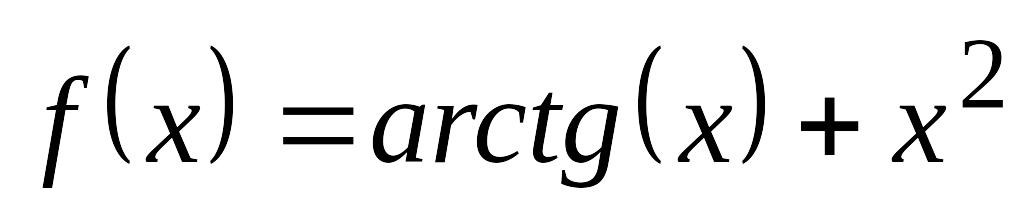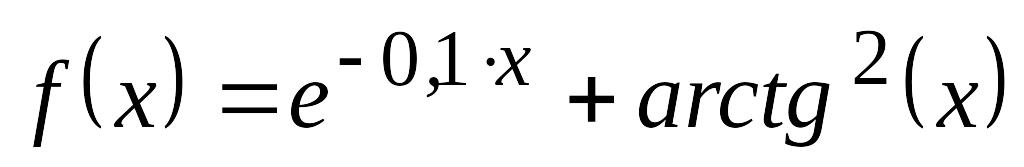5. Найти точку минимума функции с точностью 0,1, используя оптимально-пассивный поиск.

8.2 Методы многомерной оптимизации

Покоординатный спуск

В методе покоординатного спуска выбирается точка с координатами . Фиксируются все координаты кроме первой. Тогда функция является функцией одной переменной x₁. Решается одномерная задача минимизации одним из методов, изложенных в предыдущем разделе. В результате определяется точка , где принимает минимальное значение. На этом заканчивается первый шаг поиска минимума, состоящий в спускании по координате x₁. Этот процесс наглядно иллюстрируется в случае функций двух переменных. Далее фиксируются все координаты, кроме x₂ и повторяется процесс одномерной минимизации по этой координате. В результате находится точка , полученная в результате спуска по координате x₂. В результате последовательного спуска по всем остальным координатам определяется точка с координатами . На этом первая итерация заканчивается. Обозначим точку как точку с координатами . Потом процесс повторяется, начиная с координаты x₁. В результате k итераций получается последовательность точек стремящихся к точке минимума .

На практике используются следующие критерии окончания итерационного процесса:

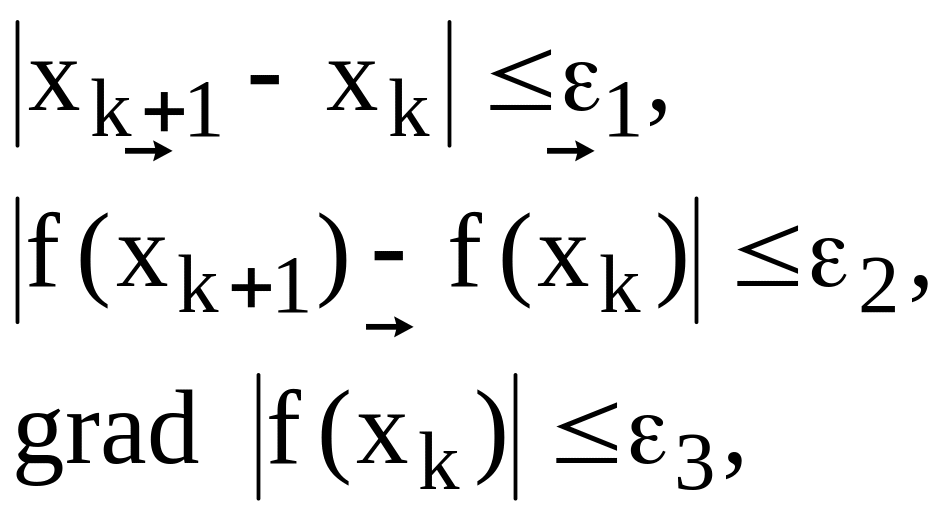(8.2) (2.9)

где ₁,₂,₃ - заданные положительные числа.

Выбирается либо один из этих критериев, либо их различные сочетания, либо все три вместе одновременно.

В методе покоординатного спуска важным является вопрос о сходимости рассмотренного процесса минимизации. Это зависит от выбора самой функции, а также от начального приближения.

Если линии уровня имеют изломы, то данный метод может оказаться быть непременным. Изломы соответствуют так называемому “оврагу” на поверхности, задаваемой уравнением U=f(x₁,x₂). На рисунке 8.3 представлены линии уровня соответствующие “оврагу”. Дно оврага соответствует пунктирной линии соединяющей изломы. Спускаясь по какой-либо координате, мы можем попасть в точку , соответствующей дну “оврага”. Проведем с одной и другой стороны от точки касательные к линии уровня. В результате мы получим две касательные из которых можно образовать сектор, имеющий угол раскрыва , который включает все направления движения от точки по которым функция f(x₁,x₂) убывает. Назовем этот сектор “сектором “оврага” убывания” функции f(x₁,x₂). Естественно движения по направлениям от точки не принадлежащим “сектору оврага” будут приводить к возрастанию функции f(x₁,x₂).

Таким образом, при покоординатном спуске возможна такая ситуация, что любое движение от точки по координатам будет происходить в направлениях, лежащих вне “сектора оврага”, т.е. приводить к возрастанию функции. Следовательно, итерационный процесс на основании признаков (8.2) закончится в точке . Спуститься ниже мы не можем, а точки минимума мы еще не достигли.

Простой градиентный метод.

Идея метода состоит в следующем. Выбирается точка и вычисляется в ней градиент функции

.

Делаем шаг в направлении обратном градиенту (рис.8.4). В результате вычисляем точку

для которой выполняется условие: . Если это условие не выполняется, то шаг h₀ уменьшают до тех пор, пока это условие не будет выполнено. Далее в точке вычисляется значение и делаем шаг h₁ в противоположном направлении и вычисляется значение .

Процесс продолжается до выполнения условия:

, или , i=1,2,...,n. (8.3)

Данный метод представляет собой полный аналог метода оптимального пассивного поиска точки минимума для функции одной переменной, там и здесь изменяется только один параметр - величина шага h.

В описанном методе требуется вычисление градиента функции на каждом шаге. Расчетные формулы для частных производных можно получить только в том случае, если функция задана аналитически. В противном случае эти производные вычисляются численно с помощью формул численного дифференцирования:

(8.4)

При использовании градиентного спуска основной объем вычислений приходится на вычисление самого градиента. Поэтому были созданы различные модификации этого метода. Одной из них является следующий метод.

Метод наискорейшего спуска.

Через точку перпендикулярно линии уровня (в направлении антиградиента) проводится прямая линия. По этой прямой двигаются до тех пор, пока функция убывает. Так как точки на этой прямой определяются уравнением:

,

где   0 - параметр, то такое движение представляет собой решение одномерной задачи минимизации функции

относительно параметра . В результате находится такое значение параметра ₁, а следовательно такая точка

,

которая соответствует минимальному значению функции на выбранной прямой.