4.1.2 Вычисление определителей и обратной матрицы

Вычисление определителей

Рассмотрим систему линейных уравнений:

Определитель системы линейных уравнений имеет вид:

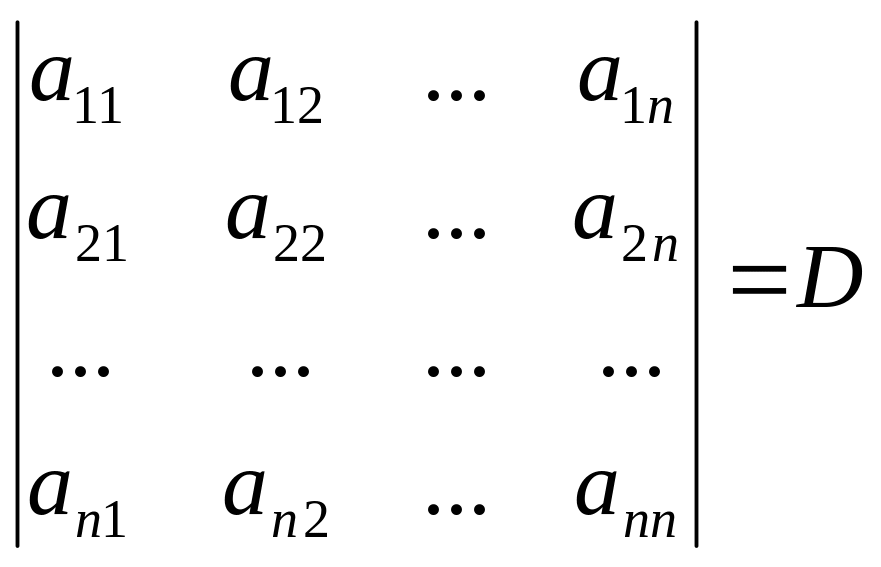(4.13)

Вычисление определителя системы линейных уравнений удобно производить методом Гаусса.

Рассмотрим, что происходит с определителем при реализации метода Гаусса:

1. Первое уравнение системы делят на элемент а₁₁ – соответственно первая строчка определителя разделится на а₁₁ , т.е.

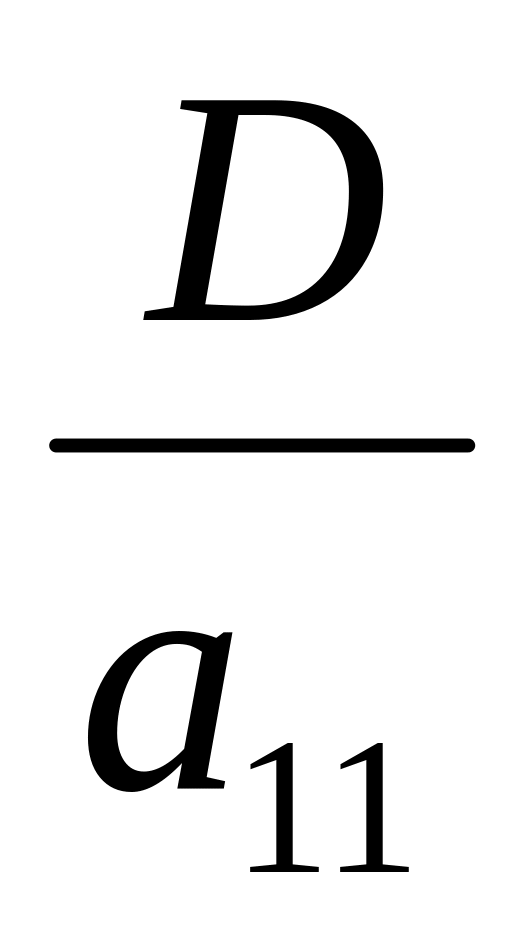
2. Преобразования, связанные с исключением х₁ (вычитание строк) величину D не меняют.

3. Второе уравнение делится на второй ведущий элемент 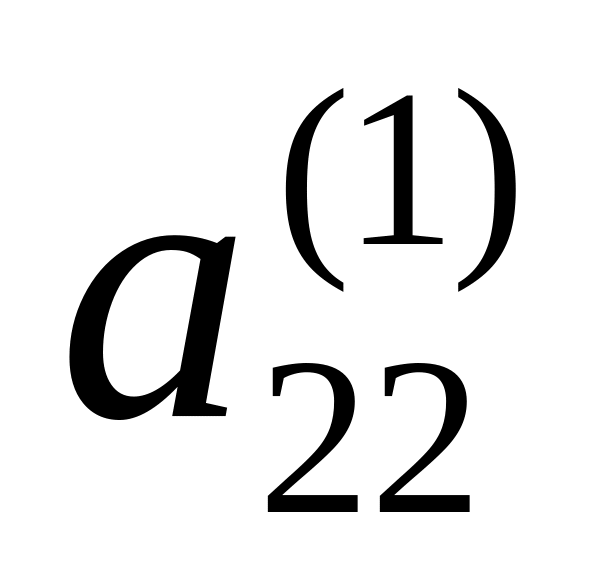, следовательно величина определителя станет

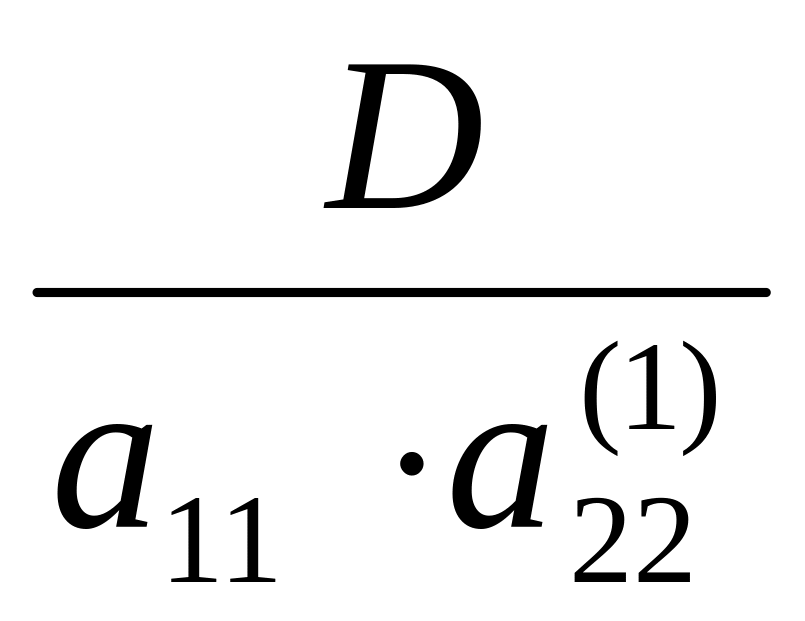
Продолжая аналогичные рассуждения на n-ом шаге приходим к треугольной системе и ее определитель равен . Поскольку определитель треугольной матрицы равен произведению элементов главной диагонали, а после преобразований получается система с единичной матрицей, определитель которой равен 1, тогда . Отсюда получаем:

(4.14),

где - ведущие элементы схемы единственного деления.

Таким образом, чтобы вычислить определитель некоторой квадратной матрицы, нужно решить систему уравнений без учета правой части и воспользоваться формулой 4.2.

Пример: Вычислить определитель:

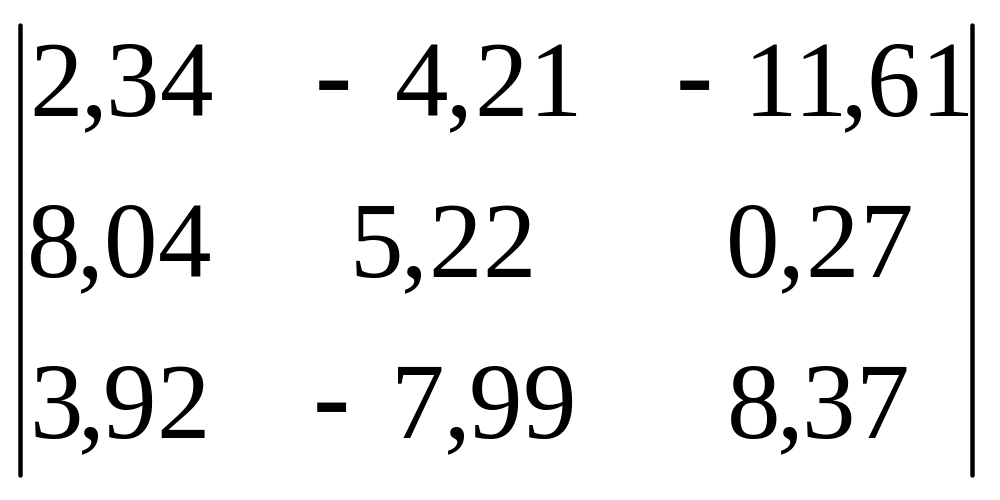
Решение:

Расчеты будем производить с использованием расчетной таблицы:

Таблица 4.2

раздел	х1	х2	х3
А	2,34 8,04 3,92	– 4,21 5,22 – 7,49	–11,61 0,27 8,37
	1	– 1,799	– 4,962
А1		19,685 – 0,938	40,161 27,819
		1	2,040
А2			29,732
			1

Ведущие элементы схемы единственного деления метода Гаусса: 2,34; 19,685; 29,732. Находим значение определителя

D = 2,34 ∙ 19,685 ∙ 29,732 = 1369,5.

Вычисление обратной матрицы

Схема единственного деления в методе Гаусса может использоваться и для нахождения обратной матрицы А^–1 для невырожденной матрицы А.

Обратной матрицей А^–1 для матрицы А называется матрица, для которой выполняется условие А· А^–1 = Е, где Е – единичная матрица.

Если представить искомую матрицу А^–1 и единичную матрицу в виде совокупности векторов-столбцов А^–1 = (х⁽¹⁾, х⁽²⁾, … , х⁽ⁿ⁾) , Е = (е⁽¹⁾, е⁽²⁾, … , е⁽ⁿ⁾), где х⁽ⁱ⁾ – i-й столбец А^–1, е⁽ⁱ⁾ – столбец, где i-й элемент равен 1, остальные нули. Тогда соотношение А· А^–1 = Е можно представить в виде совокупности n систем линейных уравнений А· х⁽ⁱ⁾ = е⁽ⁱ⁾. Решение каждой системы дает соответствующий столбец обратной матрицы.

Таким образом нахождение обратной матрицы можно выполнять в виде схемы единственного деления, заменив столбец свободных элементов столбцами единичной матрицы.

Пример: Найти обратную матрицу для А:

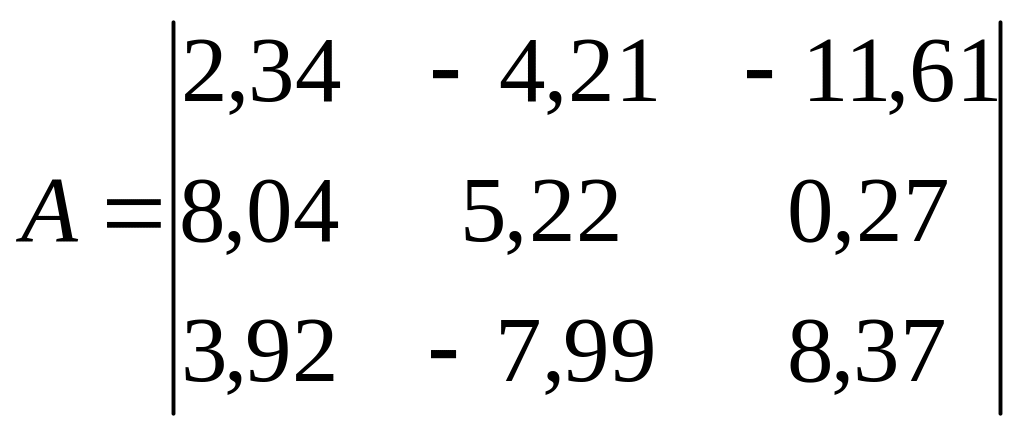
Решение:

Расчеты будем производить с использованием расчетной таблицы:

Таблица 4.3

раздел	х1j	х2j	х3j	j =1	j=2	j=3
А	2,34 8,04 3,92	– 4,21 5,22 – 7,49	–11,61 0,27 8,37	1 0 0	0 1 0	0 0 1
	1	– 1,799	– 4,962	0,427	0	0
А1		19,685 – 0,938	40,161 27,819	–3,436 –1,674	1 0	0 1
		1	2,040	–0,174	0,051	0
А2			29,732	–1,839	0,048	1
			1	–0,062	0,002	0,034
В	1	1	1	–0,062 –0,048 0,036	0,002 0,048 0,093	0,034 –0,069 0,043

Обратная матрица .

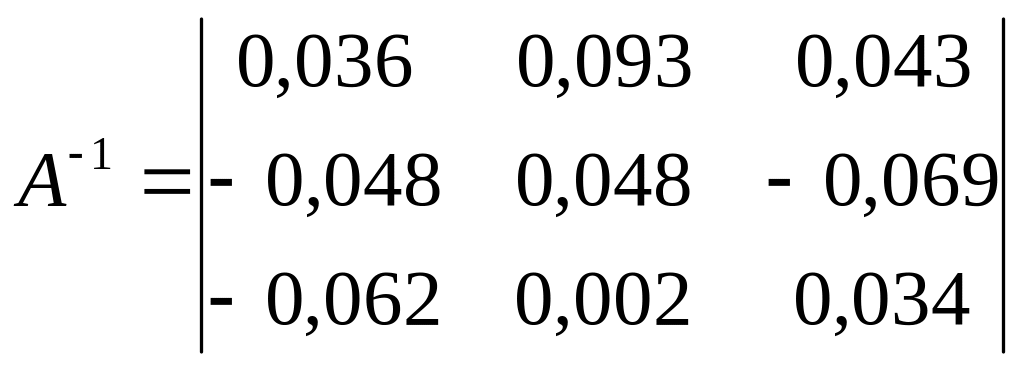Примечание: При умножении прямой и обратной матриц естественно возникновение невязок, так как в процессе вычислений возникают погрешности.