Контрольные вопросы

1. На какой идее основывается построение квадратурных формул Гаусса?

2. Что можно сказать о точности метода Гаусса?

§7. Решение обыкновенных дифференциальных уравнений

7.1. Задача численного решения обыкновенных дифференциальных уравнений

Дифференциальные уравнения - это уравнения, в которых неизвестными являются не переменные (т. е. числа), а функции одной или нескольких переменных. Эти уравнения (или системы) включают соотношения между искомыми функциями и их производными. Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями. В противном случае говорят об уравнениях в частных производных.

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида y ' = f(x, y).

Таким образом, решить (иногда употребляют другое слово проинтегрировать) дифференциальное уравнение - значит определить неизвестную функцию на определенном интервале изменения ее переменных.

Как известно, обыкновенное дифференциальное уравнение имеет единственное решение, если помимо уравнения определенным образом заданы начальные или граничные условия. Отыскание такого решения называется задачей Коши.

Задача Коши: Найти решение дифференциального уравнения, в виде функции у(х), удовлетворяющей начальному условию у(х₀) = у₀.

7.2. Методы Эйлера

В основе метода Эйлера лежит идея графического построения решения дифференциальных уравнений (рис. 7.1). Заметим, что дифференциальное уравнение совместно с начальным условием задают направление касательной к искомой интегральной кривой в точке М₀(х₀, у₀). Двигаясь вдоль этой касательной (рис. 7.1), получим приближенное значение решения в точке х₁: y₁ = у₀+ h f(x₁; y₁). Продолжая данную процедуру, можно построить прямую проходящую через данную точку (рис. 7.1), и найти приближенное значение решения в точке х₂ = х₁ + h.

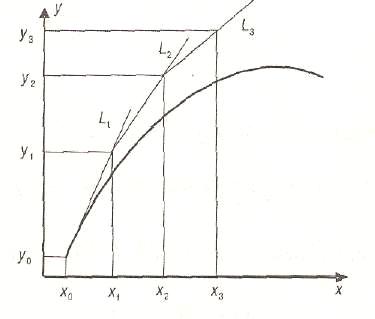
Рисунок 7.1. Графическая интерпритация метода Эйлера

Таким образом получаем формулы метода Эйлера.

Формулы Эйлера:

x_i = x₀ + ih;

∆y_i = hf(x_i; y_i);

y_i₊₁ = y_i +∆y_i (7.1) где (i = 0, 1, 2, …, n), х₀ – начальное условие, h – шаг.

Вычисления удобно оформлять в таблицу:

Таблица 7.1

i	x_i	y_i	∆y_i = hf(x_i; y_i)

Методы численного интегрирования дифференциальных уравнений, в которых решение получается от одного узла к другому, называются пошаговыми. Метод Эйлера – простейший представитель таких методов.

Погрешность метода Эйлера на каждом шаге пропорциональна h².

Оценка общей погрешности сложна, что усугубляется систематическим возрастанием погрешности с каждым шагом.

Наиболее используемым методом оценки точности является способ двойного прохождения заданного отрезка – с шагом 2h и с шагом h (метод двойных вычислений). Для удобства сопоставления, полученные значения сводят в одну таблицу:

x_i	y_i(2h)	y_i(h)

Таблица 7.2

Совпадение соответствующих десятичных знаков в полученных двумя способами результатах дает основание считать их верными.

Известны различные уточнения метода Эйлера. Модификации данных методов направлены на уточнение направления перехода из одной точки в другую. Наиболее известным из уточненных методов является метод Эйлера – Коши.

Формулы Эйлера – Коши:

x_i = x₀ + ih;

y_i+1 = y_i +∆y_i

(7.2)