Контрольные вопросы

1. По каким формулам производятся вычисления в методе Эйлера?

2. В какой форме получается приближенное решение дифференциального уравнения по методу Эйлера?

3. Что можно сказать о динамике погрешности в пошаговом методе Эйлера?

4. Что представляют собой уточненные формулы Эйлера?

5. В чем различие методов Эйлера и Рунге –Кутта? Как это различие можно охарактеризовать с графической точки зрения?

§8. Методы оптимизации

8.1 Методы одномерной оптимизации

Пусть задана функция f(x) на отрезке [a,b], график которой представлен на рис1.. Точка называется точкой глобального минимума, если выполняется условие: , для всех .

Точка называется точкой локального минимума, если существует  - окрестность этой точки, что выполняется условие

Если вместо знака неравенства или равенства стоит просто знак неравенства, то говорят, что является точкой строгого глобального или локального минимума.

Здесь, как и при решении нелинейных уравнений, вначале проводится этап локализации, т.е. определяется отрезок локализации [a,b], на котором существует только одна точка локального минимума, а затем этап итерационного уточнения. Не существует общего алгоритма определения отрезка локализации, поэтому для каждой задачи стараются либо подобрать аналогичную, но уже решенную ранее задачу, либо просто проводят вычисления и смотрят на поведение функции, т.е проводится ее предварительный анализ, чтобы оценить ее свойств.

Унимодальные функции.

Пусть функция f(x) определена на отрезке локализации [a,b] с одной точкой локального минимума . Если слева от точки минимума функция строго убывает ( , ), а справа строго возрастает ( , ), то такая функция называется унимодальной. Из этого определения следует, что унимодальная функция не обязательно непрерывна (см. рис.8.1).

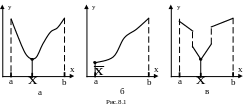
О птимально-пассивный поиск.

На отрезке локализации [a,b] с помощью точек x₀, x₁,...,x_n, строится равномерная сетка: x_i=a+ih, i=0,1,2,...,n; h=(b-a)/n и вычисляются значения функции в узлах f(x_i) (рис. 9.2). Определяется точка x _k , в которой функция принимает минимальное значение: . Точка x_k принимается за приближенное значение точки минимума: .

Оценим погрешность. Можем записать и . Точка минимума может находится только в интервале [x_k-1, x_k+1], т.к. в противном случае функция не будет унимодальной. Так как , то или . Отсюда . Следовательно для абсолютной погрешности метода оптимального пассивного поиска можем записать:

(8.1).

Алгоритм нахождения экстремумов функции методом половинного деления:

1. Находят производную заданной функции y' = f(x);

2. Если не задан отрезок [a; b], на котором необходимо найти точку экстремума, то производят отделение корней уравнения f'(x) = 0;

3. Начальное приближение точки экстремума получают по формуле:

х₀ = (a + b)/2; при этом погрешность ∆x₀ = |a – b|/2;

4. Находят значения производной f'(a), f'(b), f'(x₀);

5. Из получившихся отрезков [a; x₀] или [x₀;b] выбирают отрезок, на котором производная функции меняет знак, ему принадлежит точка экстремума;

6. Находят следующее приближение точки экстремума путем деления полученного отрезка пополам, вычисляя погрешность аналогично п.3.

7. Продолжают итерационный процесс, пока ни получат ∆x_i < ε, где ε – заданная погрешность.

8. Находят значение функции y = f(x_i) в точке экстремума.