6.5. Вычисление интеграла с использованием табличного процессора Excel.
Вычисления интеграла методом Гаусса можно производить с помощью табличного процессора Excel. В данном случае пользуются той же таблицей, что и при ручном счете. Выгода использования Excel в том, что можно увеличить количество частей, на которые разбивается отрезок интегрирования, тем самым, уменьшив погрешность результата.
Вычисления методом трапеций интеграла с помощью Excel представлено на рис. 6.5., 6.6.
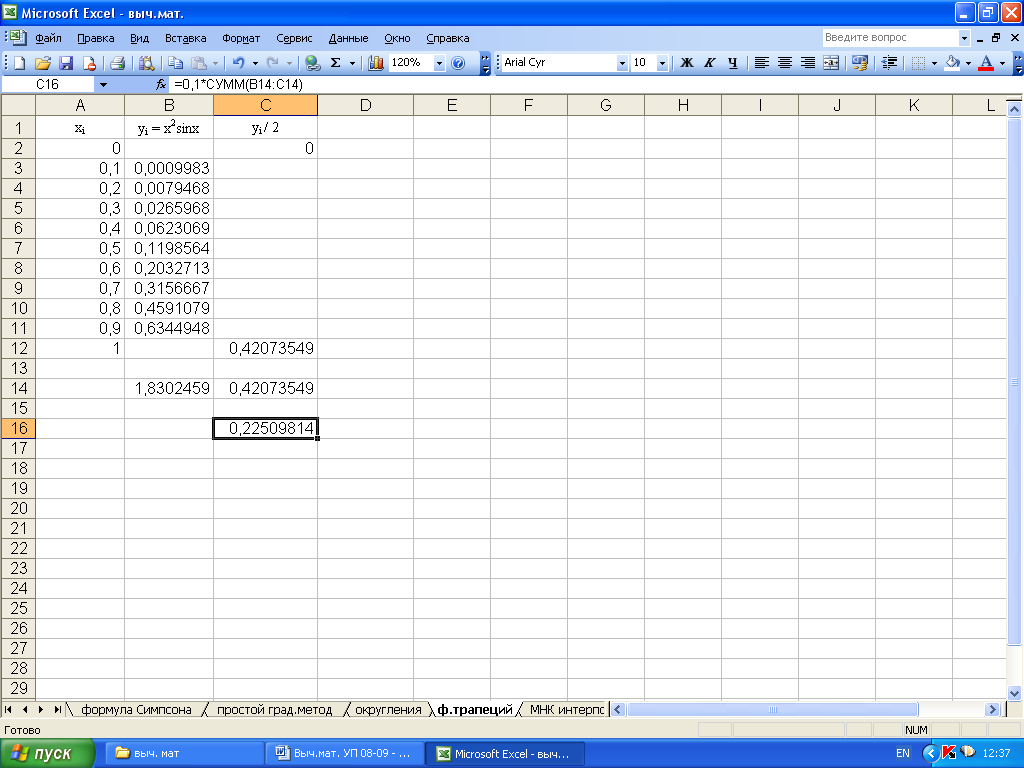
Рисунок 6.5. Вычисление интеграла методом трапеций в Excel
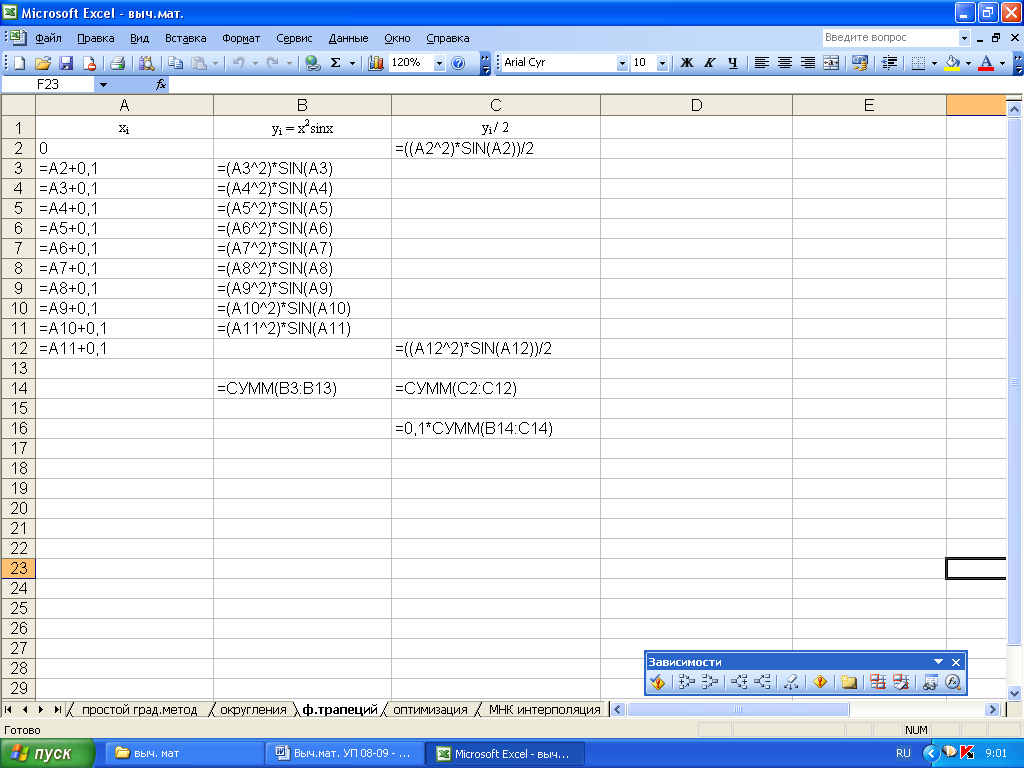
Рисунок 6.6. Вычисление интеграла методом трапеций в режиме проверки формул
Задания для самостоятельного решения
Приближенно вычислить интеграл с использованием метода Гаусса, при этом на всем отрезке интегрирования использовать четыре узла.
.
Приближенно вычислить интеграл с использованием метода Гаусса, при этом на всем отрезке интегрирования использовать пять узлов. .
Приближенно вычислить интеграл с использованием метода Гаусса, при этом на всем отрезке интегрирования использовать пять узлов. Оценить погрешность результата
.
Приближенно вычислить интеграл с использованием метода Гаусса, при этом на всем отрезке интегрирования использовать пять узлов. Оценить погрешность результата
.
Приближенно вычислить интеграл с использованием метода Гаусса, при этом на всем отрезке интегрирования использовать пять узлов. Оценить погрешность результата
Практическая работа №8
Тема: «Вычисление интегралов по формулам Гаусса»
Цели: освоение вычисления интегралов приближенными методами с помощью квадратурных формул Гаусса; сравнение методов трапеций и парабол с методом Гаусса.
Задание 1. Вычислить интеграл от заданной функции f(x) на отрезке [a; b] при делении отрезка на 10 равных частей по формуле Гаусса.
Задание 2. Вычислить интеграл от заданной функции f(x) на отрезке [a; b] при h = 0,01 с помощью математических программных средств
Задание 3. Сравнить полученный в задании 1 результат с результатами, полученными при вычислении интеграла методами трапеций и парабол.
Исходные данные:
Вариант 1. ; Вариант 2.
Вариант 3. ; Вариант 4.
Вариант 5. ; Вариант 6.
Вариант 7. ; Вариант 8.
Вариант 9. ; Вариант 10.
Вариант 11. ; Вариант 12.
Вариант 13. ; Вариант 14.
Вариант 15. ; Вариант 16.
Вариант 17. ; Вариант 18.
Вариант 19. ; Вариант 20.
Примеры выполнения заданий работы
Задание 1. Вычислить интеграл от заданной функции f(x) на отрезке [a; b] при делении отрезка на 10 равных частей по формуле Гаусса.
Решение:
Оформим вычисления в таблицу:
i |
xi |
хi1= |
хi2= |
yi (хi1) (i = 0,…,n-1) |
yi (хi2) (i = 0,..,n-1) |
0 |
0 |
0,02113249 |
0,078868 |
0,00000944 |
0,00049005 |
1 |
0,1 |
0,12113249 |
0,178868 |
0,00177304 |
0,00569215 |
2 |
0,2 |
0,22113249 |
0,278868 |
0,01072537 |
0,02140672 |
3 |
0,3 |
0,32113249 |
0,378868 |
0,3255086 |
0,05309115 |
4 |
0,4 |
0,42113249 |
0,478868 |
0,07250071 |
0,10566206 |
5 |
0,5 |
0,52113249 |
0,578868 |
0,13520907 |
0,18331848 |
6 |
0,6 |
0,62113249 |
0,678868 |
0,22452206 |
0,28938023 |
7 |
0,7 |
0,72113249 |
0,778868 |
0,34334373 |
0,42614496 |
8 |
0,8 |
0,82113249 |
0,878868 |
0,49350196 |
0,59476723 |
9 |
0,9 |
0,92113249 |
0,978868 |
0,67563779 |
0,79516236 |
10 |
1 |
|
|
|
|
|
|
|
2,28273177 |
2,47511539 |
|
= 0,1/2(2,28273177+2,47511539) = 0,22324447
Оценим погрешность: F(4)(x) = (x2– 12) sinx – 8x cosx
= 14;
= 0,223244± 0,000001.