Контрольные вопросы

1. Каким образом производится вычисление интегралов приближенными методами?

2. В чем выражается преимущество формулы парабол перед формулой трапеций?

3. Как производится оценка погрешности методов прямоугольников, трапеций, парабол?

6.4 Квадратурная формула Гаусса

В методах трапеций и парабол основной акцент делается на построение интерполяционного многочлена, выбор же узлов на исходном отрезке, с точки зрения теории, произволен. Существует, однако, иной под­ход к построению квадратурных формул, в котором центральное место играет выбор узлов для интерполирования подынтеграль­ной функции. Такой метод называется методом квадратурных формул Гаусса.

Рассмотрим его простейшую реализацию.

Традиционно при получении квадратурных формул Гаусса в исходном интеграле выполняется замена переменной, переводя­щая интеграл по отрезку [а; Ь] в интеграл по отрезку [-1; 1]:

, или

Тогда (6.8)

и можно далее, не теряя общности, развивать метод Гаусса применительно к

интегралу вида .

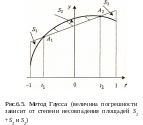Рассмотрим геометрическую интерпритацию метода (рис. 6.5).

Будем использовать простейшую (т.е. линейную) интерполяцию подынтегральной функции. Если в качестве узлов интерполяции взять концы отрезка [-1; 1], то различие в площадях криволинейной трапеции, ограниченной сверху кривой у = φ(х), и «обычной» трапеции, ог­раниченной сверху прямой, проведенной через концы указанной кривой, фиксировано видом функции у = φ(х). Одна­ко если сделать узлы интерполяции «подвижными» (рис.7.5), то можно выбрать их таким образом, чтобы разность между пло­щадями криволинейной и «обычной» трапеции была значительно меньше.

Выб­ерем значения А₁ и А₂ так, чтобы площадь трапеции, ограниченной сверху прямой, проходящей через точки А₁ (t₁, φ(t₁)) и A₂(t₁, φ(t₁)) была равна интегралу от любого многочлена некоторой (наивыс­шей возможной) степени. Поскольку положение точек А₁ и А₂ определяют четыре координаты, то этот многочлен может опре­деляться максимум четырьмя коэффициентами, т. е. является мно­гочленом 3-й степени Р₃(t) = a₀ + a₁t + a₂t² + a₃ t³.

Уравнение прямой, проходящей через точки А₁ и А₂, имеет вид

Таким образом возникает задача: выбрать t₁ и t₂ так, чтобы равенство , имело место при любых значениях a₀ , a_1, a₂ ,a₃ . При решении данной задачи следует одно из двух решений:

1) 2) .

С учетом этого и формулы (7.8), получаем формулу Гаусса в следующем виде:

(6.9)

Отметим, что формула (7.9) – лишь одна из семейства формул, называемых формулами Гаусса для вычисления интегралов. Опираясь на изложенную выше идею, можно строить квадратурные формулы, точные для любого алгебраического многочлена любой нечетной степени.

Формула для оценки погрешности:

(6.10),

где

Вычисления по формуле Гаусса (6.9) удобно оформлять в таблицу:

Таблица 6.1.

i	xi	хi1=	хi2=	yi (хi1) (i = 0,..,n-1)	yi (хi2) (i = 0,..,n-1)
				∑yi(хi1)	∑yi(хi2)