6.2 Методы прямоугольников и трапеций

Если функция f (x) на отрезке [x_i–1; x_i] заменяется полиномом нулевой степени, то приближенное значение интеграла на частичном отрезке будет иметь вид

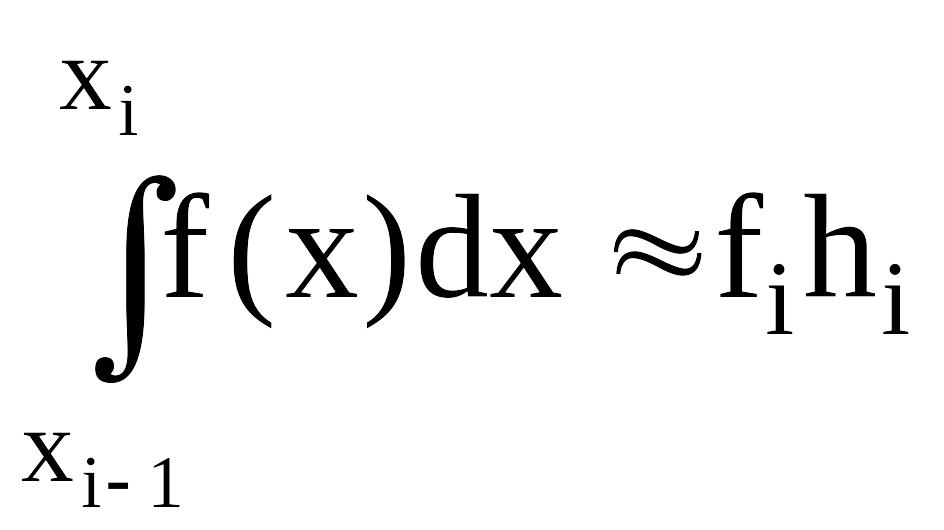, где h_i=x_i-x_i+1 , а f_i=f(_i) - значение функции в точке _i=(x_i+x_i-1)/2.

Данная формула означает, что определенный интеграл от функции f(x) на элементарном отрезке [x_i-1,x_i] приближенно равен площади прямоугольника, у которого основание равно h_i, а высота - значению функции, вычисленное в средней точке отрезка.

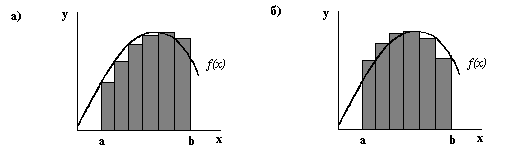
Рисунок 6.2. Геометрическая интерпритация метода прямоугольников

В зависимости от выбора точки ξ _i получаются различные формулы прямоугольников, то есть ξ _i = х _i–1 (рис.6.2 а) или ξ _i = х _i (рис. 7.2 б):

(6.1)

или (6.2)

Формулы (6.1) и (6.2) называются формулами прямоугольников.

Формула для оценки погрешности: (6.3),

где

Заменяя в частичном интеграле 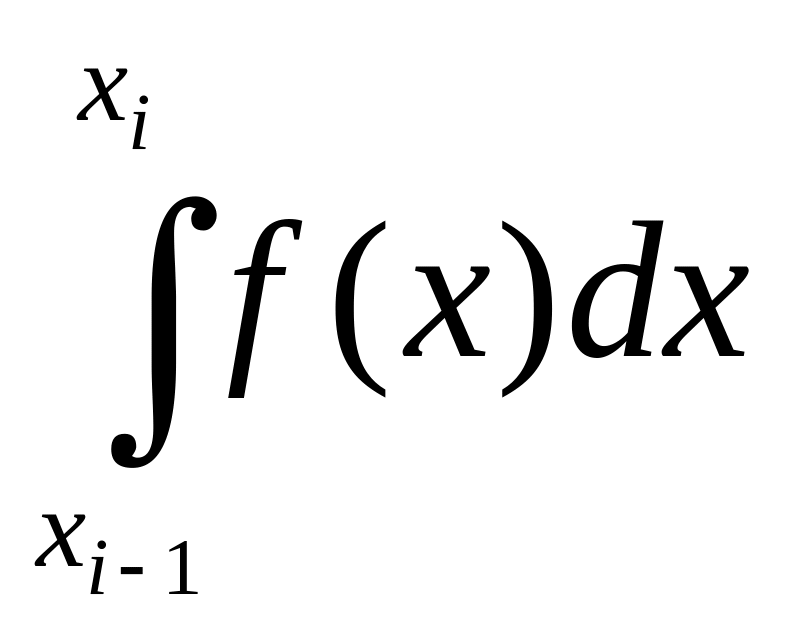функцию f (x) линейным полиномом получаем формулу трапеций на частичном отрезке (рис. 7.3)

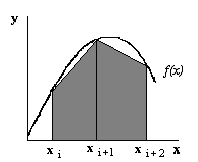
Рисунок 6.3 Метод трапеций

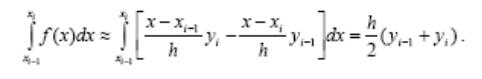
Общая формула трапеций получается суммированием частичных интегралов и имеет вид:

(6.4)

формула для оценки погрешности: (6.5),

где

6.3 Метод Симпсона (метод парабол)

Аппроксимируя в частичном интеграле функцию f (x) квадратичным полиномом Лагранжа получаем так называемую формулу Симпсона (формулу парабол) для частичного интервала.

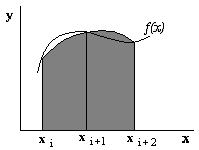
Рисунок 6.6. Метод парабол

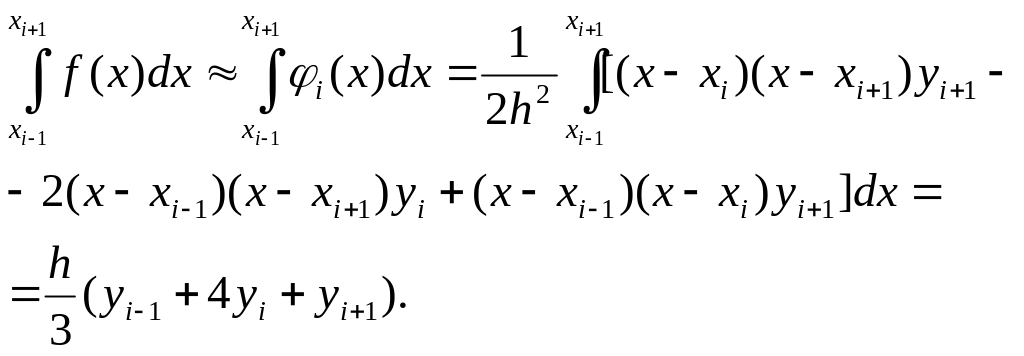
Для всего отрезка [a, b] соответственно получаем:

(6.6)

Формула для оценки погрешности: (6.7),

где

Задания для самостоятельного решения

1. Приближенно вычислить интеграл с использованием метода трапеций, при этом на всем отрезке интегрирования использовать пять узлов и в результате оставить только верные знаки.

.

2. Приближенно вычислить интеграл с использованием метода Симпсона, при этом на всем отрезке интегрирования использовать пять узлов и в результате оставить только верные знаки. .

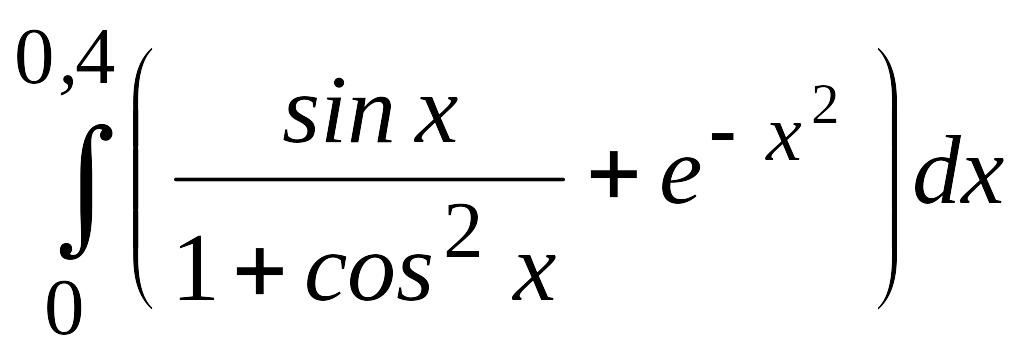3. Приближенно вычислить интеграл с использованием метода прямоугольников, при этом на всем отрезке интегрирования использовать пять узлов и в результате оставить только верные знаки. Оценить погрешность результата .

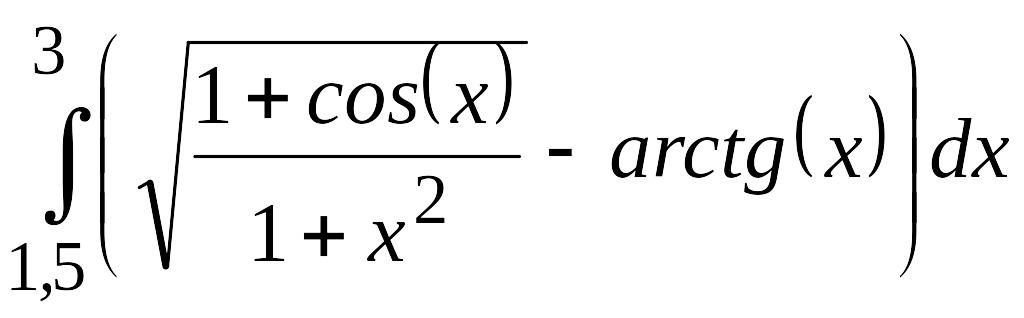4. Приближенно вычислить интеграл с использованием метода трапеций, при этом на всем отрезке интегрирования использовать пять узлов и в результате оставить только верные знаки. Оценить погрешность результата .

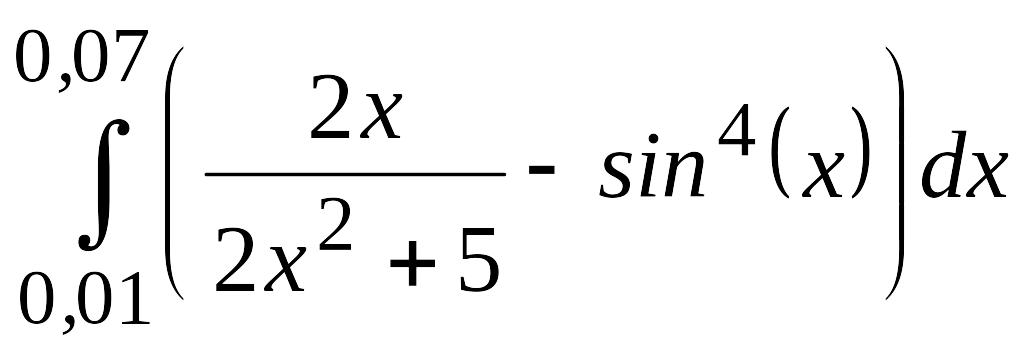5. Приближенно вычислить интеграл с использованием метода Симпсона, при этом на всем отрезке интегрирования использовать пять узлов и в результате оставить только верные знаки. Оценить погрешность результата .

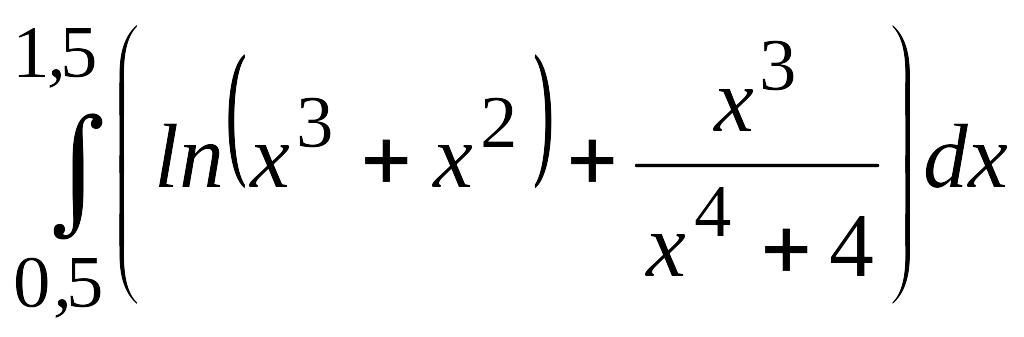Практическая работа №7

Тема: «Вычисление интегралов по формулам Ньютона-Котеса»

Цели: освоение вычисления интегралов приближенными методами прямоугольников, трапеций и с помощью формулы Симпсона - методом парабол; сравнение методов.

Задание 1. Вычислить интеграл от заданной функции f(x) на отрезке [a; b] при делении отрезка на 10 равных частей по формуле прямоугольников.

Задание 2. Вычислить интеграл от заданной функции f(x) на отрезке [a; b] при делении отрезка на 10 равных частей по формуле трапеций.

Задание 3. Вычислить интеграл от заданной функции f(x) на отрезке [a; b] при делении отрезка на 10 равных частей по формуле парабол.

Задание 4. Сравнить полученные результаты.

Исходные данные:

Вариант 1. ; Вариант 2.

Вариант 3. ; Вариант 4.

Вариант 5. ; Вариант 6.

Вариант 7. ; Вариант 8.

Вариант 9. ; Вариант 10.

Вариант 11. ; Вариант 12.

Вариант 13. ; Вариант 14.

Вариант 15. ; Вариант 16.

Вариант 17. ; Вариант 18.

Вариант 19. ; Вариант 20.