5.3 Приближение функций с помощью табличного процессора Excel
В табличном процессоре Excel для интерполяции с помощью формулы Лагранжа можно воспользоваться соответствующей таблицей (таблица 5.1).
А также для аппроксимации Excel имеет удобные встроенные средства. Самый наглядный способ – использование графического представления данных:
Необходимо ввести таблицу данных и построить по ним точечную диаграмму;
Выделив диаграмму, через главное меню выполнить команды Диаграмма Добавить линию тренда (рис. 5.1) Тренд (тенденция) – термин для обозначения линии графика аппраксимируемой функции.
В открывшемся диалоговом окне на закладке Тип необходимо выбрать один из видов функции, предлагаемых для аппроксимации (рис. 5.1). Таким образом перебирая различные виды функций можно подобрать линию тренда наиболее подходящую к заданным значениям
В том же диалоговом окне, перейдя к закладке Параметры необходимо установить галочку на флажке показывать уравнение на диаграмме – после выполнения команд на диаграмме появляется уравнение, которое соответствует линии тренда и является искомой функцией (рис. 5.2).
В закладке Параметры можно также установить галочку на флажке поместить на диаграмму величину достоверности аппроксимации R^2. В статистике данная величина называется коэффициентом детерминированности,она показывает насколько точной получилась построенная функция (рис. 5.2).
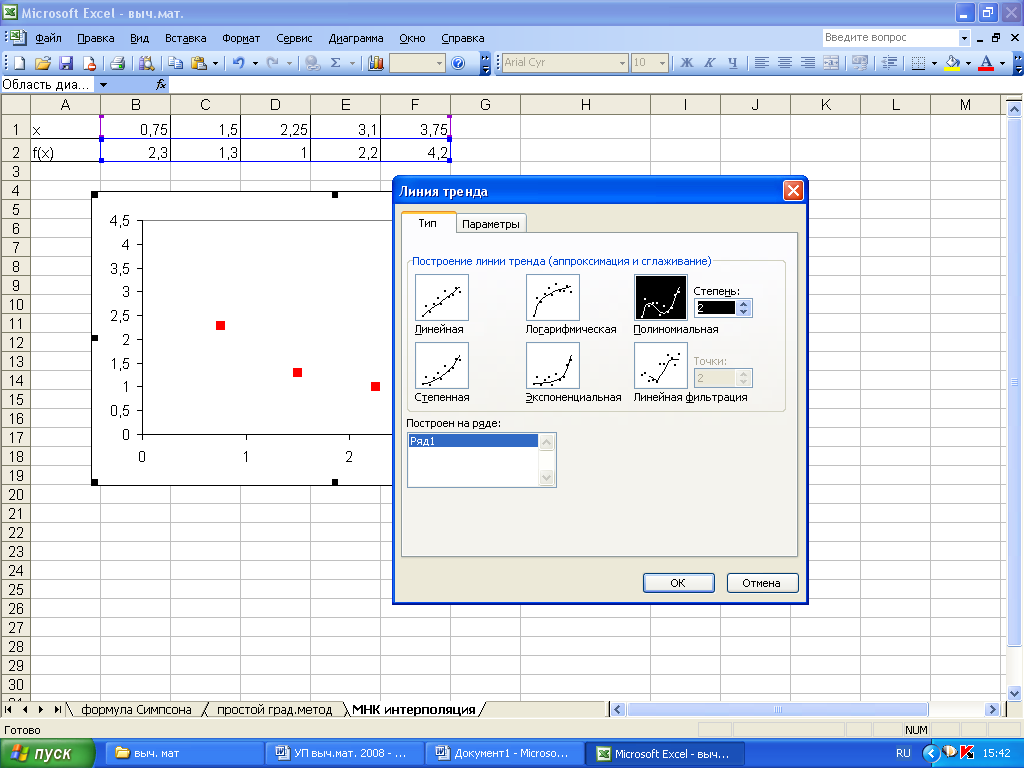
Рисунок 5.1. Получение линии тренда при аппроксимации функции в Excel
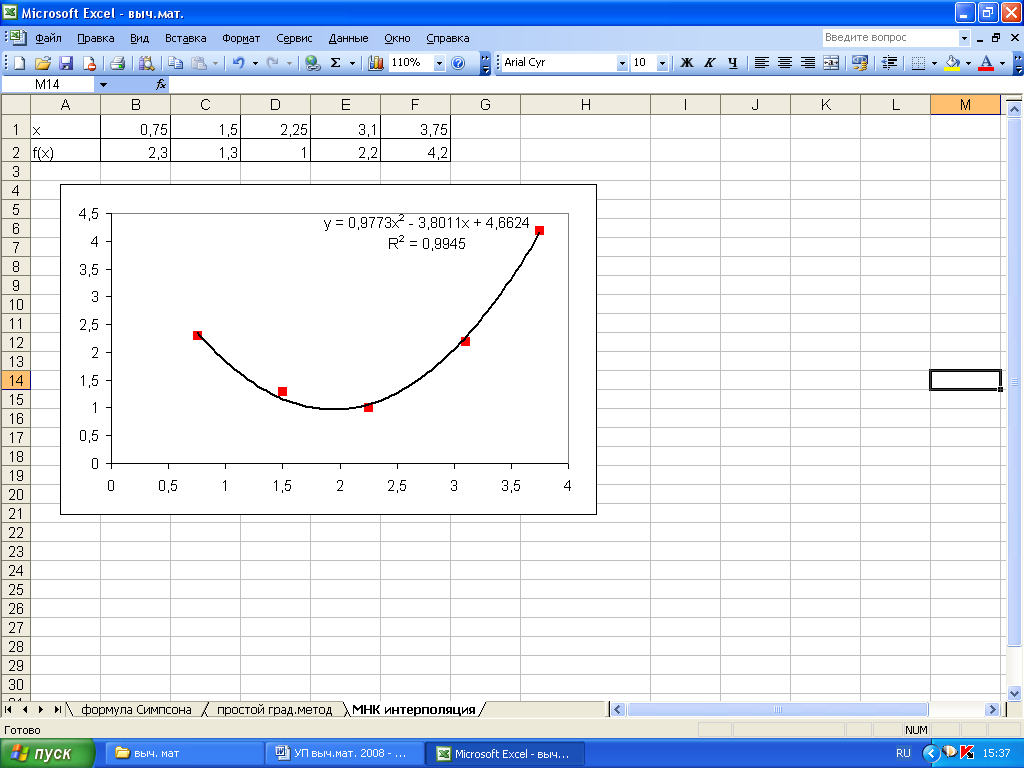
Рисунок 5.2. Результат аппроксимации функции в Excel
Интерполяцию или экстраполяцию можно получить, используя функцию ПРЕДСКАЗ в мастере функций (рис. 5.3).
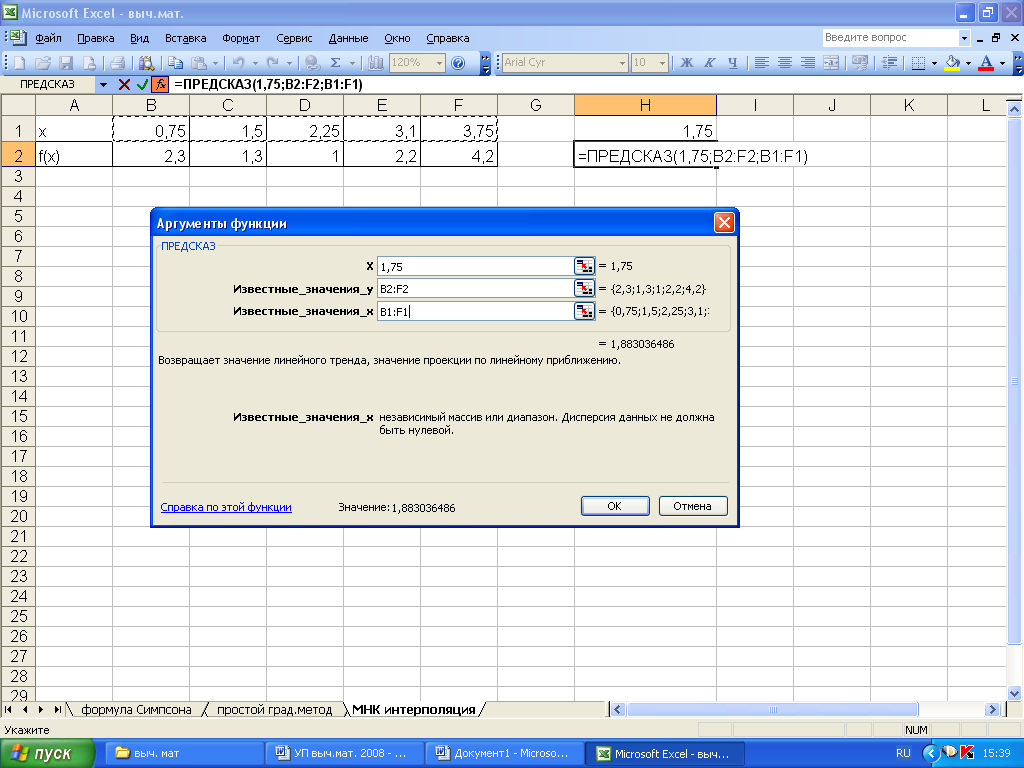
Рисунок 5.3. Нахождение интерполяционного значения функции в табличном процессоре Excel
Задания для самостоятельного решения
x |
2,0 |
2,2 |
2,4 |
2,6 |
2,8 |
3,0 |
f(x) |
8,69 |
11,44 |
14,70 |
18,53 |
22,98 |
28,10 |
x |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
f(x) |
-1,67 |
-1,80 |
-1,93 |
-2,05 |
-2,18 |
-2,30 |
Практическая работа №6
Тема: «Составление интерполяционного многочлена Лагранжа»
Цели: освоение применения интерполяционного многочлена Лагранжа для вычисления значения функции по промежуточному значению аргумента;
Задание1. Для функции, заданной таблицей узловых значений, составить формулу интерполяционного многочлена Лагранжа, вычислить с его помощью одно значение функции для промежуточного значения аргумента х*.
Исходные данные для задания 1:
Вариант 1. х* = 0,7
х |
-1 |
0 |
3 |
4 |
f(x) |
-3 |
5 |
2 |
-6 |
Вариант 2. х* = 2,4
х |
2 |
3 |
5 |
6 |
f(x) |
4 |
1 |
7 |
2 |
Вариант 3. х* = 0,7
х |
0 |
2 |
3 |
5 |
f(x) |
-1 |
-4 |
2 |
-8 |
Вариант 4. х* = 7,3
х |
7 |
9 |
13 |
15 |
f(x) |
2 |
-2 |
3 |
-4 |
Вариант 5. х* = 3,6
х |
-3 |
-1 |
3 |
5 |
f(x) |
7 |
-1 |
4 |
-6 |
Вариант 6. х* = 1,7
х |
1 |
2 |
4 |
7 |
f(x) |
-3 |
-7 |
2 |
8 |
Вариант 7. х* = 2,7
х |
2 |
4 |
5 |
7 |
f(x) |
9 |
-3 |
6 |
-2 |
Вариант 8. х* = 0,7
х |
-4 |
-2 |
0 |
3 |
f(x) |
2 |
8 |
5 |
10 |
Вариант 9. х* = 2,8
х |
2 |
4 |
7 |
8 |
f(x) |
-1 |
-6 |
3 |
12 |
Вариант 10. х* = 0,7
х |
0 |
1 |
4 |
6 |
f(x) |
7 |
-1 |
8 |
2 |
Вариант 11. х* = 2,7
Х |
-1 |
-1 |
2 |
4 |
f(x) |
4 |
9 |
1 |
6 |
Вариант 12. х* = 3,4
Х |
-1 |
1,5 |
3 |
5 |
f(x) |
4 |
-7 |
1 |
-8 |
Вариант 13. х* = – 4,5
Х |
-9 |
-7 |
- 4 |
-1 |
f(x) |
3 |
-3 |
4 |
-9 |
Вариант 14. х* = 1,3
Х |
-8 |
-5 |
0 |
2 |
f(x) |
9 |
-2 |
4 |
6 |
Вариант 15. х* = –3,6
Х |
-7 |
-5 |
- 4 |
-1 |
f(x) |
4 |
- 4 |
5 |
10 |
Вариант 16. х* = 2,7
Х |
1 |
4 |
9 |
11 |
f(x) |
-2 |
9 |
3 |
-7 |
Вариант 17. х* = 8,5
Х |
7 |
8 |
9 |
13 |
f(x) |
6 |
-2 |
7 |
-10 |
Вариант 18. х* = 0,7
Х |
-4 |
0 |
2 |
5 |
f(x) |
4 |
8 |
-2 |
-9 |
Вариант 19. х* = 2,8
Х |
-3 |
-1 |
1 |
3 |
f(x) |
11 |
-1 |
6 |
-2 |
Вариант 20. х* = 0,7
х |
0 |
3 |
8 |
11 |
f(x) |
1 |
5 |
- 4 |
-8 |
Задание 2. Вычислить значение заданной функции f(x) для промежуточного значения аргумента х* по интерполяционному многочлену Лагранжа с помощью вычислительной таблицы. Сравните результат интерполирования со значением функции, которое вычислите, используя ее аналитическое выражение.
Задание 3. Для таблично заданной функции получить эмпирическую формулу с помощью математических программных средств (табличный процессор Excel). Сравнить полученную формулу с заданным аналитическим выражением.
Исходные данные для задания 2, 3:
Вариант 1.
х*
= 3,8
х |
1,3 |
2,1 |
3,7 |
4,5 |
6,1 |
7,7 |
8,5 |
f(x) |
1,7777 |
4,5634 |
13,8436 |
20,3952 |
37,3387 |
59,4051 |
72,3593 |
Вариант 2.
х*
= 3,5
х |
1,2 |
1,9 |
3,3 |
4,7 |
5,4 |
6,8 |
7,5 |
f(x) |
0,3486 |
1,0537 |
1,7844 |
2,2103 |
2,3712 |
2,6322 |
2,7411 |
Вариант 3.
х*
= 0,5
х |
-3,2 |
-0,8 |
0,4 |
2,8 |
4,0 |
6,4 |
7,6 |
f(x) |
-1,9449 |
-0,6126 |
0,3097 |
1,8068 |
2,0913 |
1,4673 |
0,6797 |
Вариант 4. х* = 4,8
х |
1,3 |
2,1 |
3,7 |
4,5 |
6,1 |
7,7 |
8,5 |
f(x) |
1,7777 |
4,5634 |
13,8436 |
20,3952 |
37,3387 |
59,4051 |
72,3593 |
Вариант 5. х* = 4,1
х |
1,3 |
2,1 |
3,7 |
4,5 |
6,1 |
7,7 |
8,5 |
f(x) |
1,7777 |
4,5634 |
13,8436 |
20,3952 |
37,3387 |
59,4051 |
72,3593 |
Вариант 6. х* = 3,9
х |
1,2 |
1,9 |
3,3 |
4,7 |
5,4 |
6,8 |
7,5 |
f(x) |
0,3486 |
1,0537 |
1,7844 |
2,2103 |
2,3712 |
2,6322 |
2,7411 |
Вариант 7. х* = 3,3
х |
-3,2 |
-0,8 |
0,4 |
2,8 |
4,0 |
6,4 |
7,6 |
f(x) |
-1,9449 |
-0,6126 |
0,3097 |
1,8068 |
2,0913 |
1,4673 |
0,6797 |
Вариант 8. х* = 4,0
х |
1,3 |
2,1 |
3,7 |
4,5 |
6,1 |
7,7 |
8,5 |
f(x) |
1,7777 |
4,5634 |
13,8436 |
20,3952 |
37,3387 |
59,4051 |
72,3593 |
Вариант 9. х* = 2,9
х |
1,3 |
2,1 |
3,7 |
4,5 |
6,1 |
7,7 |
8,5 |
f(x) |
1,7777 |
4,5634 |
13,8436 |
20,3952 |
37,3387 |
59,4051 |
72,3593 |
Вариант 10. х* = 5,3
х |
1,2 |
1,9 |
3,3 |
4,7 |
5,4 |
6,8 |
7,5 |
f(x) |
0,3486 |
1,0537 |
1,7844 |
2,2103 |
2,3712 |
2,6322 |
2,7411 |
Вариант 11. х* = 4,1
х |
-3,2 |
-0,8 |
0,4 |
2,8 |
4,0 |
6,4 |
7,6 |
f(x) |
-1,9449 |
-0,6126 |
0,3097 |
1,8068 |
2,0913 |
1,4673 |
0,6797 |
Вариант 12. х* = 6,6
х |
1,2 |
1,9 |
3,3 |
4,7 |
5,4 |
6,8 |
7,5 |
f(x) |
0,3486 |
1,0537 |
1,7844 |
2,2103 |
2,3712 |
2,6322 |
2,7411 |
Вариант 13. х* = 4,4
х |
1,3 |
2,1 |
3,7 |
4,5 |
6,1 |
7,7 |
8,5 |
f(x) |
1,7777 |
4,5634 |
13,8436 |
20,3952 |
37,3387 |
59,4051 |
72,3593 |
Вариант 14. х* = 5,2
х |
-3,2 |
-0,8 |
0,4 |
2,8 |
4,0 |
6,4 |
7,6 |
f(x) |
-1,9449 |
-0,6126 |
0,3097 |
1,8068 |
2,0913 |
1,4673 |
0,6797 |
Вариант 15. х* = 3,7
х |
1,2 |
1,9 |
3,3 |
4,7 |
5,4 |
6,8 |
7,5 |
f(x) |
0,3486 |
1,0537 |
1,7844 |
2,2103 |
2,3712 |
2,6322 |
2,7411 |
Вариант 16. х* = 0,4
х |
1,3 |
2,1 |
3,7 |
4,5 |
6,1 |
7,7 |
8,5 |
f(x) |
1,7777 |
4,5634 |
13,8436 |
20,3952 |
37,3387 |
59,4051 |
72,3593 |
Вариант 17. х* = 7,5
х |
-3,2 |
-0,8 |
0,4 |
2,8 |
4,0 |
6,4 |
7,6 |
f(x) |
-1,9449 |
-0,6126 |
0,3097 |
1,8068 |
2,0913 |
1,4673 |
0,6797 |
Вариант 18. х* = 2,5
х |
1,2 |
1,9 |
3,3 |
4,7 |
5,4 |
6,8 |
7,5 |
f(x) |
0,3486 |
1,0537 |
1,7844 |
2,2103 |
2,3712 |
2,6322 |
2,7411 |
Вариант 19. х* = 6,8
х |
1,3 |
2,1 |
3,7 |
4,5 |
6,1 |
7,7 |
8,5 |
f(x) |
1,7777 |
4,5634 |
13,8436 |
20,3952 |
37,3387 |
59,4051 |
72,3593 |
Вариант 20. х* = – 1,7
х |
-3,2 |
-0,8 |
0,4 |
2,8 |
4,0 |
6,4 |
7,6 |
f(x) |
-1,9449 |
-0,6126 |
0,3097 |
1,8068 |
2,0913 |
1,4673 |
0,6797 |