5.2 Интерполяционный многочлен Лагранжа

Наиболее распространенными является интерполирование многочленами.

Пусть функция y = f(x) задана таблично:

хi	x0	x1	…	xi	…	xn
yi	y0	y1	…	yi	…	yn

Общий вид интерполяционного многочлена Лагранжа:

(5.1)

Погрешность формулы Лагранжа есть R _n (x) =f (x) −L _n (x) .

Получаем выражение для погрешности формулы Лагранжа:

, (5.2) где П_n+1(x) = (х– х₀)(х– х₁)· … · (х– х_n)

Пример. Используя интерполяционный многочлен Лагранжа вычислить в указанных точках и значения функции , заданной в виде таблицы:

0	0,5	-0,5
1	1,5	0,7
2	2,5	0,3

и оценить погрешность для заданного значения третьей производной .

Решение:

Будем использовать многочлен Лагранжа 2-ой степени:

.

Погрешность интерполяции с помощью этого многочлена Лагранжа вычисляется как:

.

Значение функции в точках и , используя многочлен Лагранжа, будет равно:

для

для

.

Абсолютная погрешность интерполяции:

при равна:

при равна:

Относительная погрешность интерполяции:

при равна:

при равна:

Применение формулы Лагранжа приводит к большому числу однотипных вычислений, поэтому вычислять значения функции, по многочлену Лагранжа, удобнее с использованием вычислительной таблицы (табл. 6.1)

Таблица 6.1

х = х*	х0	х1	х2	…	рi	yi	yi / pi
х0	х*– х0	х0– х1	х0– х2	…	р0	y0	y0 / p0
х1	х1– х0	х*– х1	х1– х2	…	р1	y1	y1 / p1
х2	х2– х0	х2– х1	х* –х2	…	р2	y2	y2 / p2
…	…	…	…	…	…	…	…
							S=Σ(yi / pi)

р_i – произведение разностей по строкам: р_i = (х^*– х₀)(х₀– х₁)· … · (х₀– х_n)

Многочлен Лагранжа имеет вид:

L_n(x) = S ∙ (х^*– х₀)( х^*– х₁)( х^* –х₂)∙ … · (х^* – х_n).

Задания для самостоятельного решения

1. Используя интерполяционный многочлен Лагранжа вычислить в указанных точках и значения функции , заданной в виде таблицы:

0	0,0	0,1
1	0,8	0,3
2	1,6	0,3

и оценить погрешность для заданного значения третьей производной .

2. Используя интерполяционный многочлен Лагранжа вычислить в указанных точках и 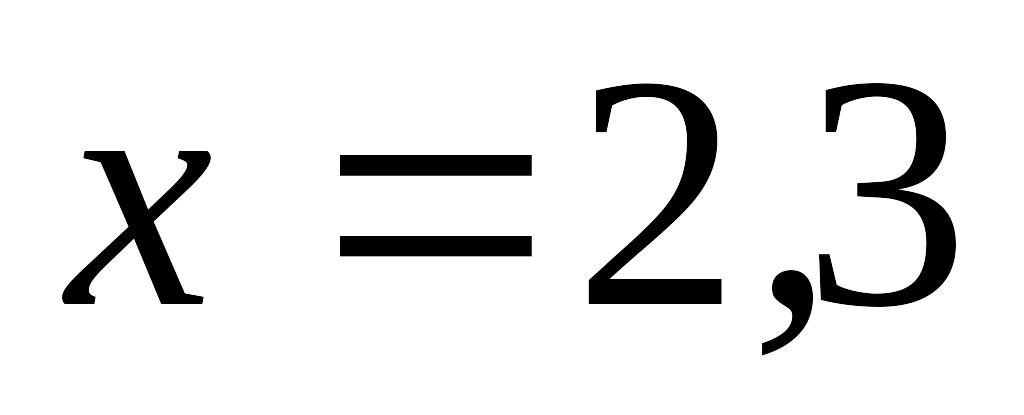значения функции , заданной в виде таблицы:

0	3,5	0,2
1	6,5	0,5
2	9,5	-0,9

и оценить погрешность для заданного значения третьей производной .

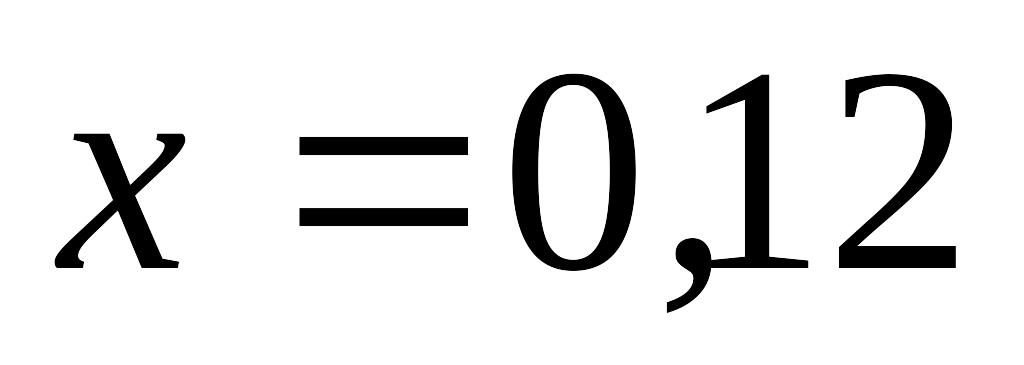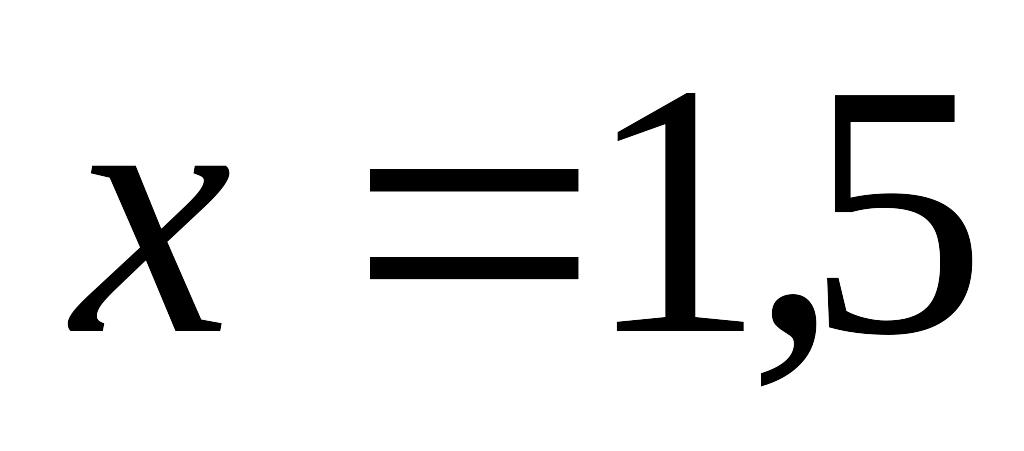3. Используя интерполяционный многочлен Лагранжа вычислить в указанных точках и значения функции , заданной в виде таблицы:

0	0,1	-7,5
1	1,5	-0,67
2	2,0	7,3

и оценить погрешность для заданного значения третьей производной .

4. Используя вычислительную схему Лагранжа вычислить в указанных точках и значения функции , заданной в виде таблицы:

0	0,0	1,0
1	0,5	-1,7
2	1,0	-0,5

5. Используя вычислительную схему Лагранжа вычислить в указанных точках и значения функции , заданной в виде таблицы:

0	1,0	-0,5
1	3,5	-2,2
2	6,0	-0,6