Задания для самостоятельного решения
Вычислить определитель и найти обратную матрицу А–1:
.
Вычислить определитель и найти обратную матрицу А–1:
.
Вычислить определитель и найти обратную матрицу А–1, используя программные средства:
.
Вычислить определитель и найти обратную матрицу А–1, используя программные средства:
.
Вычислить определитель и найти обратную матрицу А–1, используя программные средства:
.
Контрольные вопросы.
1. К какой категории методов вычислительной математики относится метод Гаусса?
2. Каков алгоритм метода Гаусса?
3. Какого рода вычислительные ошибки отслеживает контроль вычислений при использовании метода Гаусса в табличной форме?
4. Каким образом метод Гаусса используется для вычисления определителя, нахождения обратной матрицы?
4.1.3 Итерационные методы решения систем линейных уравнений. Метод простой итерации
Алгоритм метода простой итерации:
Исходную систему приводят к системе с преобладающими диагональными коэффициентами и к виду Х = АХ;
Проверяют условия сходимости:
,
,
(4.15).За начальные значения берут столбец свободных членов;
Точность результата устанавливают по формуле:
(4.16),
где ρ зависит от α:
,
,
.
Метод Зейделя
Основная идея метода Зейделя в том, что на каждом итерационном шаге при вычислении значения xi учитываются уже полученные на данном шаге значения x1, x2,…, xi-1.
4.2. Решение системы уравнений и вычисление определителя с помощью табличного процессора Excel
Решение системы уравнений
Для решения системы уравнений может быть использовано средство, предназначенное для решения задач оптимизации. Это средство – Поиск решения. Предварительно для каждой переменной отводят по ячейке. Например, в выше приведенном примере три переменных, следовательно отводят три ячейки, например, А1, В1, С1. В каждую из этих ячеек заносят значение 0.
В какие либо другие ячейки вводят формулы для вычисления левых частей уравнения (по одной формуле в ячейку). Например, в ячейку А2: = 2,34*А1– 4,21*В1– 14,61*С1, аналогично в ячейку А3 – формулу для вычисления левой части второго уравнения, А4 – третьего уравнения.
Так же необходимо ввести целевую функцию – сумму всех переменных.
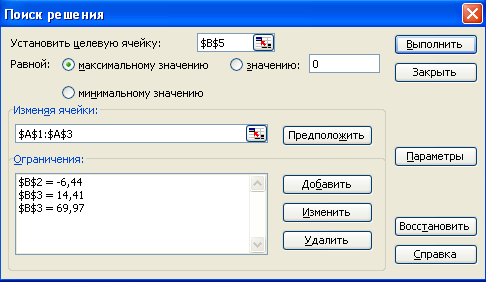
Рисунок 4.1. Подготовка к решению системы уравнений в Excel посредством опции Поиск решения
После этого запускают Поиск решения в меню Сервис. В появившемся диалоговом окне щелкают по кнопке Добавить – открывается окно Добавление ограничения, в которое необходимо внести ограничение, т.е. правую часть уравнения. Например, для первого уравнения: в Ссылку на ячейку нужно ввести номер ячейки, в которой находится левая часть уравнения – А2, из меню посередине нужно выбрать знак «=», в Ограничение вводят значение правой части: 14,41. Аналогично для каждого уравнения.
Щелкнув Выполнить в Поиске решения получают значения переменных в ячейках А1, В1, С1.
Для решения системы линейных уравнений в Excel также можно использовать метод Гаусса в виде схемы единственного деления (табл.4.1) или методы простой итерации и Зейделя выполняя расчеты непосредственно.
Вычисление определителя
Для вычисления определителя в Excel можно использовать схему единственного деления (табл. 4.2) или вычислять определитель непосредственно.
Однако в Excel есть специальное средство для нахождения определителя матрицы. Определитель можно вычислить с использованием мастера функций при помощи функции МОПРЕД. Для этого необходимо ввести матрицу, в свободной ячейке ввести функцию МОПРЕД, где в качестве массива выделить диапазон ячеек матрицы (рис. 4.2)
Рисунок 4.2. Вычисление определителя в Excel посредством функции МОПРЕД