3.6. Решение уравнений с помощью табличного процессора Excel

Excel для решения уравнений располагает специальным средством Подбор параметра в меню Сервис. Его алгоритм скрыт от пользователя, но если важен именно результат, а не путь к нему, то обращение к стандартному средству оправдано.

В ячейке А1 записывается начальное значение х₀.

В ячейке В1– левая часть уравнения.

После открытия Подбор параметра в меню Сервис, появляется диалоговое окно, куда вносятся следующие сведения:

Установить в ячейке – В1;

Значение ­– 0 (т.к. решение уравнения - это нахождение значения х при нулевом значении функции)

Изменяя значение ячейки – А1 (меняются значения переменной).

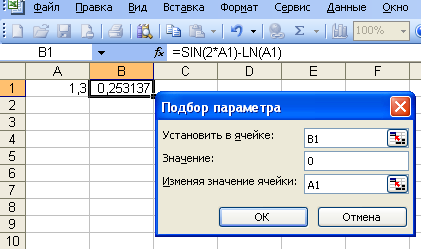
Рисунок 3.6. Подготовка к решению уравнения в Excel посредством опции

Подбор параметра

После нажатия ОК, появляется диалоговое окно, где под надписью Текущее значение можно видеть значение функции, наиболее близкое к нулю, для которого найдено значение х.

Корень уравнения появляется в ячейке В1.

Задания для самостоятельного решения

1. Найдите все корни уравнения методом касательных с точностью 0,001: .

2. Найдите все корни уравнения методом касательных с точностью 0,001: .

3. Найдите наименьший положительный корень уравнения методом хорд с точностью 0,001: .

4. Найдите все корни уравнения методом хорд с точностью 0,001: .

5. Найдите все корни уравнения, используя компьютерные программные средства (табличный процессор Excel, MATCAD, MATLAB): .

Практическая работа №3

Тема: «Решение уравнений методами Ньютона»

Цели: освоение решения алгебраических и трансцендентных уравнений методом касательных и методом хорд; сравнение методов.

Задание 1. Найдите один из кореней заданного уравнения, с погрешностью ε = 0,001 методом касательных;

Задание 2. Найдите один из кореней заданного уравнения, с погрешностью ε = 0,001 методом хорд;

Задание 3. Сравните метод касательных и метод хорд, а также данные методы с методом простой итерации.

Задание 4. Используя компьютерные программные средства (табличный процессор Excel, MATCAD, MATLAB) вычислите все корни заданного уравнения.

Исходные данные:

Вариант 1 0,008x³ – cos x = 0

Вариант 2

Вариант 3 х – 10 sin x = 0

Вариант 4 8 cos x – x – 6 = 0

Вариант 5 ln(x + 6,1) – 2 sin(x – 1,4) = 0

Вариант 6 2 ^{– х} – sin x =0

Вариант 7 lg (x+5) – cos x = 0

Вариант 8

Вариант 9 2 ^x – 2cos x = 0

Вариант 10 x∙sin x – 1 = 0

Вариант 11 10 cos x - 0,1x² = 0

Вариант 12 3 sin 8x – 0,7x + 0,9 = 0

Вариант 13 1,2 – ln x – 4 cos 2x = 0

Вариант 14 sin x – 0,2x = 0

Вариант 15 4 cos x + 0,3x = 0

Вариант 16 2 lg (x+7) – 5sin x = 0

Вариант 17 2x² – 5 – 2^x = 0

Вариант 18 1,2x⁴ + 2x³ – 13x² –14,2x – 24,1 = 0

Вариант 19 2^–x –10 + 0,5x² = 0

Вариант 20 4x⁴ – 6,2 – cos(0,6x) = 0

Примеры выполнения заданий работы

Задание 1. Найдите один из кореней заданного уравнения, с погрешностью ε = 0,001 методом касательных;

sin 2x – ln x = 0; [1,3; 1,4]

Решение:

1. F(x) = sin 2x – ln x

F'(x) = 2cos 2x – 1/ x

Получаем итерационную формулу:

2. F''(x) = – 4sin 2x + 1/ x²

F(1,3) 0,25; F''(1,3) – 1,47 знаки не совпадают

F(1,5) – 0,26; F''(1,5) – 0,12 знаки совпадают

значит х₀ = 1,5

3.

4. Итерационный процесс удобно оформлять в виде таблицы:

n	xn
0	1,5	1,4001209	0,0007
1	1,4001209	1,399428	0,000001

Ответ: х = 1, 3994 ± 0,0001

Задание 2. Найдите один из кореней заданного уравнения, с погрешностью ε = 0,001 методом хорд;

sin 2x – ln x = 0; [1,3; 1,4]

Решение:

1. F''(x) = – 4sin 2x + 1/ x²

F(1,3) 0,25; F''(1,3) – 1,47 знаки не совпадают

F(1,5) – 0,26; F''(1,5) – 0,12 знаки совпадают

значит с = 1,5,

х₀ = 1,3

2. F(с) = F(1,5) = sin 2∙1,5 – ln 1,5 = – 0,264345

Итерационная формула:

3. Значение m вычисляется так же как в методе касательных, m = 2,4

n	xn
0	1,3	1,397834	0,002
1	1,397834	1,399410	0,00002

Ответ: х = 1, 3994 ± 0,0001