Определение ускорения силы тяжести с помощью оборотного маятника

Постановка задачи. Оборотный маятник с расстоянием между опорами L (рис.12.2), подвешенный на опоре 1, совершает колебания с периодом Т₁, а подвешенный на опоре 2 - колебания с периодом Т₂. Перемещением груза В₁ найти такое положение этого груза на стержне, при котором периоды Т₁=Т₂=Т. Определить соответствующее положение груза В₁, ускорение силы тяжести.

Указания к решению. Запишем соотношение (12.4) для оборотного маятника, подвешенного на опорах 1 и 2 соответственно:

(12.7)

Из теоремы Гюйгенса-Штейнера находим

(12.8)

Здесь I₀ - момент инерции физического маятника относительно оси, проходящей через центр масс.

Найдя такое положение груза В₁ на штанге, при котором Т₁=Т₂=Т, из (12.7) и (12.8) находим значение периода колебаний Т:

(12.9)

Учитывая, что l₁+ l₂=L (рис. 12.2), из (12.9) находим ускорение силы тяжести

(12.10)

Определение положения центра тяжести физического маятника

Постановка задачи. Оборотный маятник с расстоянием между опорами, равным L, подвешенный на опоре 1, совершает колебания с периодом Т₁. Если маятник подвесить на опору 2, то период колебаний оказывается равным Т₂. Определить расстояние от первой опоры до центра масс маятника.

Указания к решению. Используя формулу (12.4), получим

. (12.11)

Если маятник перевернуть и подвесить его на опоре 2, то момент инерции маятника относительно оси, проходящей через опору 2, станет равным.

(12.12)

Здесь L-l₁=l₂ - расстояние от опоры 2 до центра масс маятника. Используя теорему Гюйгенса-Штейнера, найдем

. (12.13)

Из (12.13) получим соотношение

. (12.14)

Из (12.11) и (12.12) имеем

. (12.15)

Приравнивая правые части (12.14) и (12.15), получим формулу для определения расстояния от первой опоры до центра масс маятника

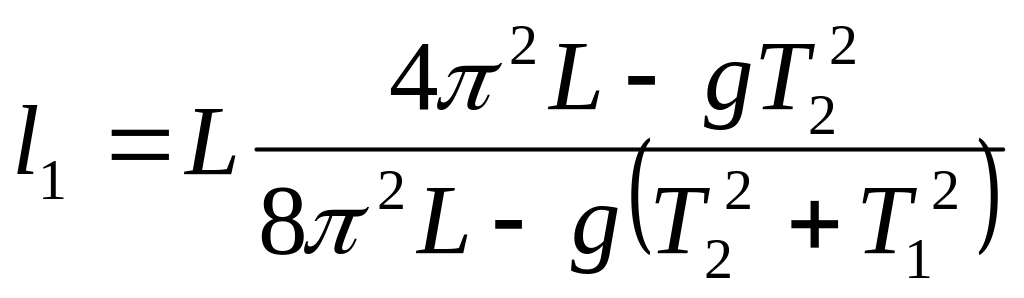. (12.16)

Экспериментальное определение момента инерции тела сложной формы методом малых колебаний

Постановка задачи. Определить момент инерции оборотного маятника, совершающего малые колебания относительно горизонтальной оси. Точка подвеса оборотного маятника фиксирована.

Указания к решению. Отклоним оборотный маятник на малый угол (рис.12.2). Тогда момент силы, действующей на маятник, равен моменту сил тяжести. Сила тяжести приложена в центре масс (в точке С), находящейся на расстояние l₁ от точки подвеса (см. задачу 12.2). Момент силы тяжести относительно горизонтальной оси вращения, проходящей через точку 0 при малых углах отклонения, будет

Используя основные уравнения вращательного движения

1. момент инерции, - угловое ускорение )

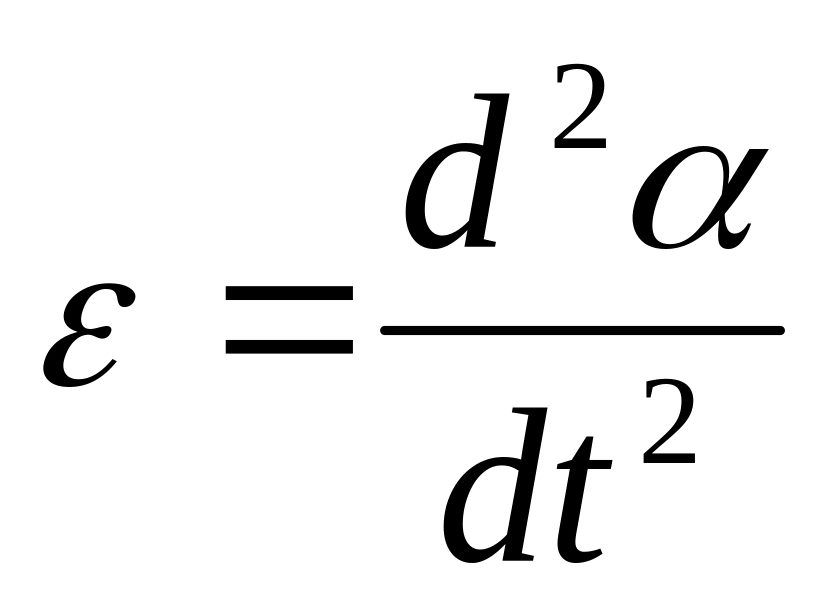и отмечая, что в проекции на ось 0z, перпендикулярную рисунку, знаки  и М противоположны, получим

. (12.17)

Непосредственной подстановкой можно убедиться, что решение дифференциального уравнения (12.17) может быть представлено в форме

. (12.18)

где ₀- угол, соответствующий максимальному отклонению маятника, ₀t- фаза колебаний в момент времени Т. Здесь ₀-собственная частота колебаний маятника. Так как косинус - периодическая функция с периодом 2, получаем

. (12.19)

Из (12.19) находим момент инерции оборотного маятника

. (12.20)