28. Регрессионный анализ

Если расчёт корреляции характеризует силу связи между двумя переменными, то регрессионный анализ служит для определения вида этой связи и дает возможность для прогнозирования значения одной (зависимой) переменной отталкиваясь от значения другой (независимой) переменной.

•  Чтобы вызвать регрессионный анализ в SPSS, выберите в меню Analyze... (Анализ) Regression... (Регрессия)

Откроется соответствующее подменю.

Разделы этой главы соответствуют опциям вспомогательного меню. Причём при изучении линейного регрессионного анализа снова будут проведено различие между простым анализом (одна независимая переменная) и множественным анализом (несколько независимых переменных). Собственно говоря, никаких принципиальных отличий между этими видами регрессии нет, однако простая линейная регрессия является простейшей и применяется чаще всех остальных видов.

Рис. 16.1: Вспомогательное меню Regression (Регрессия)

Для проведения линейного регрессионного анализа зависимая переменная должна иметь интервальную (или порядковую) шкалу. В то же время, бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа. Если зависимая переменная является категориальной, но имеет более двух категорий, то здесь подходящим методом будет мультиномиальная логистическая регрессия. Новшеством в 10 версии SPSS является порядковая регрессия, которую можно использовать, когда зависимые переменные относятся к порядковой шкале. И, наконец, можно анализировать и нелинейные связи между переменными, которые относятся к интервальной шкале. Для этого предназначен метод нелинейной регрессии.

Методы криволинейного приближения, весовые оценки и 2-ступенчатые наименьшие квадраты исследуют соответственно приближённость пути прохождения кривых при помощи компенсационных кривых, регрессионный анализ для изменяющейся дисперсии и проблемы из области эконометрии.

Переменные:

1. Предсказывающие переменные (предикаторы) или независимые переменные (факторы) – такие переменные, для которых обычно можно устанавливать желаемые значения (например, начальную температуру или скорость подачи катализатора), либо те, которые можно наблюдать, но не управлять ими (например, влажность воздуха).

2. Зависимые переменные или переменные-отклики.

В результате преднамеренных изменений или изменений, происшедших с независимыми переменными случайно, появляется эффект, который передается на другие переменные, на отклики (например, на окончательный цвет или чистоту хим продукта).

Разделение на предикаторы и отклики не всегда вполне четко и иногда зависит от наших целей. Однако роли переменных обычно легко различимы.

Общее описание модели регрессии:

Смысл РА (регрессионный анализ): РА устанавливает функциональные связи между зависимой переменной (У) и независимыми переменными (Хi), где i принадлежит (1;n), где

Х-входная переменная; регрессор.

У- регрессанд, функция отклика.

Х, У – количественные переменные.

Если i=1, то анализ однофакторный (парная регрессия)

Если i от 2 до n, то многофакторный (множественная регрессия).

1. Однофакторная модель регрессионного анализа: Y = α₀ + α_iX + ξ

У – зависимая переменная (Пр.: выручка от реализации т,р,у).

Х – независимая переменная (Пр.: цена за 1 ед.)

Альфа – параметры модели (коэффициенты).

Эпсила – случайная составляющая, с мат ожиданием = 0 и сигмой квадрат (дисперсией) = константе. Подчинена нормальному закону распределения.

2. Многофакторная модель: Y = α₀ + α₁X₁ + α₂X₂ + ... + α_NX_i + ξ, _N=от 0, _i от 1.

Х1,2, _i – экзогенные переменные (вызванные внешними причинами).

Если эпсила постоянна, то явление называется гомоскедастичность. Если нет – гетеро.

Если присутствует взаимосвязь между X_i явлениями, то называется мультиколлиниарность.

Чем меньше факторов в модели – тем она более точная. Ошибка репрезентативности (это разница между значением показателя, полученного по выборке, и генеральным параметром) – имеем дело с выборкой, а результаты исследования переносим на ген совокупность, поэтому в модели присутствует епсила.

Выбор линии регрессии: МНК.

МНК используется для оценки параметров (коэффициентов а₀ и а₁) модели. Суть метода: оценить коэффициенты модели таком образом, чтоб сумма квадрата ошибок индивидуальных значений признака у от теоретич у с крышечкой – была минимальной. Цель - минимизировать квадраты отклонений линии регрессии от наблюдаемых точек.

По этим данным строим диаграмму рассеяния

1. П ример для однофакторного анализа:

(yi – ŷ)2 = (yi – a0 – a1xi)2  min

У с крышечкой – предсказанное значение (теоретическое).

На пример. У –выручка: 10; 5; 20. Х – цена: 5; 2; 1. Находим: у_ср. и х_ср.: 11,6 и 3 соответсвенно. Строим еще 4 столбца со значениями:

• у – у_ср.: -2;-7;8.

• х – х_ср.: 2;-1;-2.

• (х – х_ср.)*(у – у_ср.): -4;7;-16. Сумм= -13

• (х – х_ср.)²: 4;1;4. Сумм=9.

Далее по формуле: Y = α₀ + α_iX + ξ, находим:

• Альфа1 = -13/ 9= -1,44.

• Альфа0 = 11,6 – (-1,44)*3 = 16,32

Выходит модель следующего вида: ŷ = 16,32 – 1,44*х.

Правильность расчёта параметров уравнения регрессии может быть проверена сравниванием сумм ∑у = ∑ŷ .

Оценка модели с помощью МНК: Далее строим по ней график прямой. Откладываем точки на оси «выручка», «цена». И какая точка будет наиболее приближена к графику, та вариация и несет наименьшую ошибку. Либо по формуле: у – ŷ = е (ошибка, остаток, находится для каждого у подставляя х). е стремится к минимуму.

2. Для линейной функции:

x	1	2	3	4	5	6
y	5,2	6,3	7,1	8,5	9,2	10,0

На опыте получены значения x и y, сведенные в таблицу. Найти прямую по методу наименьших квадратов.

Решение. Находим:

Σ x_i=21, Σ y_i=46,3, Σ x_i²=91, Σ x_iy_i=179,1.

91a+21b=179,1, 21a+6b=46,3, отсюда находим a=0,98 b=4,3.

3. А также матричным способом (например, для многофакторной модели), путем транспонирования матрицы. При учете того, что матрица содержит столько строк, сколько пар наблюдений. Содержит столбцов, сколько коэффициентов в модели (х1,х2,хн, у). Каждый столбец матрицы это, что находится при коэффициенте в модели.

Простая регрессия представляет собой регрессию между двумя переменными

—у и х, т.е. модель вида

, где у — результативный признак; х - признак-фактор.

Множественная регрессия представляет собой регрессию результативного

признака с двумя и большим числом факторов, т. е. модель вида

Коэффициент детерминации

Статистический показатель, отражающий объясняющую способность уравнения регрессии и равный отношению суммы квадратов регрессии SSR к общей вариации SST:

,

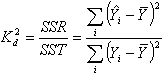где – уровень ряда, – смоделированное значение, – среднее по всем уровням ряда.

Данный показатель является статистической мерой согласия, с помощью которой можно определить, насколько уравнение регрессии соответствует реальным данным.

Коэффициент детерминации изменяется в диапазоне от 0 до 1. Если он равен 0, это означает, что связь между переменными регрессионной модели отсутствует, и вместо нее для оценки значения выходной переменной можно с таким же успехом использовать простое среднее ее наблюдаемых значений. Напротив, если коэффициент детерминации равен 1, это соответствует идеальной модели, когда все точки наблюдений лежат точно на линии регрессии, т.е. сумма квадратов их отклонений равна 0. На практике, если коэффициент детерминации близок к 1, это указывает на то, что модель работает очень хорошо (имеет высокую значимость), а если к 0, то это означает низкую значимость модели, когда входная переменная плохо "объясняет" поведение выходной, т.е. линейная зависимость между ними отсутствует. Очевидно, что такая модель будет иметь низкую эффективность