14. Критерий Фишера

F - критерий Фишера является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов. Эмпирическое значение критерия  вычисляется по формуле:

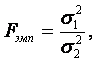
где - большая дисперсия, - меньшая дисперсия рассматриваемых вариационных рядов.

         Если вычисленное значение критерия Fэмп больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными. Иными словами, проверяется гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H0={Dx=Dy}.

         Критическое значение критерия Фишера следует определять по специальной таблице, исходя из уровня значимости α и степеней свободы числителя (n1-1) и знаменателя (n2-1).

         Проиллюстрируем применение критерия Фишера на следующем примере. Дисперсия такого показателя, как стрессоустойчивость для учителей составила 6,17 (n1=32), а для менеджеров 4,41 (n2=33) (однородность – люди делятся по 1 признаку – профессия?). Определим, можно ли считать уровень дисперсий примерно одинаковым для данных выборок на уровне значимости 0,05 (0,05 - это вероятность, связанная с F-распределением, станд).

         Для ответа на поставленный вопрос определим эмпирическое значение критерия:  При этом критическое значение критерия Fкр(0,05;31;32)=2.

         Таким образом, Fэмп=1,4<2=Fкр, поэтому нулевая гипотеза о равенстве генеральных дисперсий на уровне значимости 0,05 принимается.

Fрасч>Fтабл, то принимается Н1. Если Fрасч<Fтабл, то принимается Н0.

Однородность=отсутсвие различий в выборках:

Нулева́я гипо́теза — гипотеза, которая проверяется на согласованность с имеющимися выборочными (эмпирическими) данными. Часто в качестве нулевой гипотезы выступают гипотезы об отсутствии взаимосвязи или корреляции между исследуемыми переменными, об отсутствии различий (однородности) в распределениях (параметрах распределений) двух и/или более выборках. В стандартном научном подходе проверки гипотез исследователь пытается показать несостоятельность нулевой гипотезы, несогласованность её с имеющимися опытными данными, то есть отвергнуть гипотезу. При этом подразумевается, что должна быть принята другая, альтернативная (конкурирующая), исключающая нулевую, гипотеза. Используется при статистической проверке.

Стандартная ошибка коэффициента регрессии

Для оценки существенности коэффициента регрессии его ве­личина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n- 2).

Стандартная ошибка параметра а:

Значимость линейного коэффициента корреляции проверя­ется на основе величины ошибки коэффициента корреляции т_r:

Общая дисперсия признака х:

Коэф. регрессии Его величина показывает ср. изменение результата с изменением фактора на 1 ед.

Ошибка аппроксимации:

Проверка нулевой гипотезы

Признаки А и В будут независимыми, если значение, принятое признаком А не влияет на вероятности возможных значений признака В:

P(B_j/A_i) = P(B_i) или P(A_i,B_j) = P(A_i) P(B_j) (6.1)

Значения использованных вероятностей нам неизвестны, однако, по теореме Бернулли, при большом объеме выборки (n   ) частоты в ячейках таблицы сопряженности будут являться оценками этих вероятностей. При выполнении гипотезы о независимости признаков справедливо

p_ij = p_i.  p._j , (6.2)

где следующие величины трактуются как ожидаемые частоты:

,

(замена индекса точкой означает результат суммирования по этому индексу). Тогда проверка нулевой гипотезы сводится к оценке, насколько близки значения фактических и ожидаемых частот, т.е.

. (6.3)

Методы сравнения эмпирических (H) и теоретических (T) частот по А. Брандту (А. Brandt) и Г. Снедекору (G. Snedecor) основываются на расчете критерия согласия  ², оценивающего меру близости по всем ячейкам таблицы сопряженности:

. (6.4)

Если в конкретном опыте величина  ² оказывается чрезмерно большой, то приходится признать, что ожидаемые частоты слишком сильно отличаются от наблюдаемых. Ответ на естественный вопрос, о том, какие значения статистики следует считать чрезмерно большими, дает теорема К. Пирсона – Р. Фишера, из которой следует:

• для независимых признаков при неограниченном росте числа наблюдений распределение случайной величины  ² стремится к распределению “хи-квадрат”;

• гипотезу о независимости можно принять, если  ² не превосходит критического для заданного уровня табличного значения с (r–1)(s–1) степенями свободы;

• для зависимых признаков  ² неограниченно возрастает с увеличением n.

В 1934 г. Ф. Иэйтс (F. Yates) предложил ввести в выражение для статистики  ² так называемую поправку на непрерывность, которая связана с тем, что непрерывные распределения хи-квадрат и, соответственно, нормальное распределение используются для представления дискретных выборочных частот. С учетом такой поправки данное выражение примет следующий вид:

. (6.5)