Критерий хи-квадрат с поправкой на правдоподобие

Альтернативой формуле Пирсона для вычисления критерия хи-квадрат является поправка на правдоподобие:

При большом объеме выборки формула Пирсона и подправленная формула дают очень близкие результаты. В нашем примере критерий хи-квадрат с поправкой на правдоподобие составляет 23,688.

Тест Мантеля-Хэнзеля

Дополнительно в таблице сопряженности под обозначением linear-by-linear ("линейный-по-линейному") выводится значение теста Мантеля-Хэнзеля (20,391). Эта форма критерия хи-квадрат с поправкой Мантеля-Хэнзеля — еще одна мера линейной зависимости между строками и столбцами таблицы сопряженности. Она определяется как произведение коэффициента корреляции Пирсона на количество наблюдений, уменьшенное на единицу:

Полученный таким образом критерий имеет одну степень свободы. Метод Мантеля-Хэнзеля используется всегда, когда в диалоговом окне Crosstabs: Statistics установлен флажок Chi-square. Однако для данных, относящихся к с номинальной шкале, этот критерий неприменим.

Методы проверки статистических гипотез:

С помощью статистических критериев:

t – критерий Стьюдента, используется для установления сходства-различия средних

арифметических значений в двух выборках или в более общем виде, для установления сходства-

различия двух эмпирических распределений;

F – критерий Фишера, используется для установления сходства-различия дисперсий в

двух независимых выборках;

Q – критерий Розенбаума, используется для оценки различий между двумя выборками по

уровню какого-либо признака, количественно измеренного.

T – критерий Вилкоксона, применяется для сопоставления показателей, измеренных в

двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить

направленность изменений, и их выраженность.

χ2-критерий Пирсона, используется:

1) для сопоставления эмпирического распределения признака с теоретическим –

равномерным, нормальным или каким-то иным;

2) для сопоставления двух, трех или более эмпирических распределений одного и того же

признака.

Нулева́я гипо́теза — гипотеза, которая проверяется на согласованность с имеющимися выборочными (эмпирическими) данными. Часто в качестве нулевой гипотезы выступают гипотезы об отсутствии взаимосвязи или корреляции между исследуемыми переменными, об отсутствии различий (однородности) в распределениях (параметрах распределений) двух и/или более выборках. В стандартном научном подходе проверки гипотез исследователь пытается показать несостоятельность нулевой гипотезы, несогласованность её с имеющимися опытными данными, то есть отвергнуть гипотезу. При этом подразумевается, что должна быть принята другая, альтернативная (конкурирующая), исключающая нулевую, гипотеза. Используется при статистической проверке.

24. Проверка гипотезы о независимости признаков (таблица сопряженности признаков)

Предположим, имеется большая совокупность объектов, каждый из которых обладает двумя признаками А и В; признак А имеет m уровней: A₁, ..., A_m, а признак В – k уровней: B₁, ..., B_k . Пусть уровень А_i встречается с вероятностью P(A_i), а уровень B_j - c вероятностью P(B_j). Признаки А и В независимы, если

P(A_i B_j) = P(A_i) P(B_j), i = 1, ..., m, j = 1, ..., k ,                                                                     (10)

т.е. вероятность встретить комбинацию A_i B_j равна произведению вероятностей. Пусть признаки определены на n объектах, случайно извлеченных из совокупности; n _ij - число объектов, имеющих комбинацию A_i B_j, =n. По совокупности наблюдений {n _ij } (таблица m x k) требуется проверить гипотезу Н о независимости признаков А и В. Задача сводится к случаю с неизвестными параметрами; ими являются вероятности

P(A_i), i = 1, ..., m;  P(B_j), j = 1, ..., k,

всего (m-1) + (k-1); их оценки:

,

(в обозначениях точка означает суммирование по соответствующему индексу), и статистика (6) принимает вид:

.                             (11)

Если гипотеза Н верна, то по теореме Фишера асимптотически распределена по закону хи-квадрат с числом степеней свободы

f = mk - 1 - (m - 1) - (k - 1) = (m - 1)(k - 1),

и потому, если

,                                           (12)

то гипотезу о независимости признаков следует отклонить.

Ясно, что по (11) - (12) можно проверять независимость двух случайных величин, разбив диапазоны их значений на m и k частей.

Пример 4. Данные [2], собранные по ряду школ, относительно физических недостатков школьников (P₁, P₂, P₃ - признак А) и дефектов речи (S₁, S₂, S₃ - признак В) приведены в таблице 4. В таблице 5 даны частоты.

Таблица 4.

Таблица 5. Таблица частот

	S1 S2 S3	Сумма
P1 P2 P3	45 26 12 32 50 21 4 10 17	83 103 31
Сумма	81 86 50	217

Для проверки гипотезы о независимости этих двух признаков вычислим статистику (11): = 34.88; число степеней свободы f = (3-1) x (3-1) = 4; минимальный уровень значимости

;

это значит, что при независимых признаках вероятность получить значение такое же, как в опыте или большее, меньше 0.001, и потому гипотезу о независимости следует отклонить.

Таблица сопряженности - средство представления совместного распределения двух переменных, предназначенное для исследования связи между ними. Таблица сопряженности является наиболее универсальным средством изучения статистических связей, так как в ней могут быть представлены переменные с любым уровнем измерения.

Строки таблицы сопряженности соответствуют значениям одной переменной, столбцы - значениям другой переменной (количественные шкалы предварительно должны быть сгруппированы в интервалы).

Пр.:

Таблицы сопряженности используются для проверки гипотезы о наличии связи между двумя признаками ( Статистическая связь, Критерий "хи-квадрат" Пирсона ), а также для измерения тесноты связи ( Коэффициент фи, Коэффициент контингенции, Коэффициент Крамера).

Оценка силы связи

Как всегда в статистике, интерес исследователя не ограничивается принятием гипотезы, оценивающей величину риска предположения о существовании связи. Если признаки оказались взаимосвязаны (т.е. гипотеза об их независимости была проверена и отвергнута) представляет интерес оценка силы связи, которую хочется видеть в некотором привычном интервале величин, например, от –1 до +1 с нулевым значением при отсутствии связи. Сама по себе такая постановка проблемы определенным образом дискуссионна. Достаточно сказать, что нет единого мнения даже у соавторов настоящей книги: один из нас считает приоритетным при оценке силы связи уютный коэффициент корреляции Пирсона r (суть – долю факториальной вариации), а другой – статистики Фишера или  ² (то же, но только с учетом степеней свободы), напрямую связанные с фундаментальными для статистики уровнями значимости.

В случае таблиц сопряженности для измерения силы связи предложены десятки формул [Миркин, Розенберг, 1979; Миркин и др., 1989], которые можно свести к трем основным группам:

• традиционные коэффициенты связи, основанные на  ² ;

• меры и статистики, основанные на рангах;

• коэффициенты, измеряющие информационную связь между факторами.

Коэффициенты связи, основанные на  ² , исходят из предпосылки о том, что, чем больше объем выборки m, тем легче получить статистически значимую величину критерия даже при очень слабой взаимосвязи переменных (т.е. при больших объемах выборки даже слабые связи будут статистически значимыми).

Чтобы элиминировать влияние объема выборки m , К. Пирсон предложил в качестве меры связи среднеквадратическую сопряженность (он же – редуцированный коэффициент корреляции)

, (6.6)

который изменяется в диапазоне от 0 до min(r – 1, s – 1).

Стремясь нормировать меру связи к единому диапазону, С. Крамер видоизменил формулу (6.6) для своего коэффициента Крамера:

, (6.7)

верхний предел которого единица.

А.А. Чупров нашел для похожей формулы более звучное название – полихорический коэффициент сопряженности (коэффициент Чупрова):

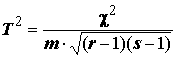. (6.8)

Нетрудно заметить, что T ² и V ² эквивалентны, когда число столбцов равно числу строк, в иных случаях V ² всегда больше, чем T ² . Для таблицы 2х2 обе меры равны  ².

Наконец, можно упомянуть еще один коэффициент, связанный с именем К. Пирсона – коэффициент контингенции:

. (6.9)

Перечисленные коэффициенты, основанные на  ² , остаются неизменными при перестановке местами строк или столбцов таблицы и всегда выражаются положительными числами, поэтому уяснение направления зависимости должно производиться только по виду таблицы сопряженности.

Коэффициенты, основанные на рангах, позволяют извлечь информацию о направлении связи между признаками, используя понятие коррелируемости на основе подсчета числа пар объектов с взаимно возрастающими, взаимно убывающими и равными значениями признаков.

Коэффициент  Кендалла учитывает число пар с равными признаками и может достигать значений -1 и +1, отражающих высшую степень положительной или отрицательной корреляции между признаками. Обычно вычисляется два варианта статистики Кендалла:  _b и  _c, которые различаются только способом обработки совпадающих рангов.

Если в данных имеется много совпадающих значений, предпочтительнее  -статистика Гудмана-Кендалла, которая представляет собой нормированную разность между вероятностью P того, что ранговый порядок двух переменных совпадает, и вероятностью Q того, что он не совпадает:

 = (P - Q)/(P + Q).

Таким образом,  -статистика в основном эквивалентна  Кендалла, за исключением того, что совпадения явно учитываются в нормировке.

Коэффициент d Соммера аналогичен коэффициенту  с дифференциальным учетом пар с равными значениями признаков. Вычисляются два значения коэффициента, учитывающих равенство первого d(A|B), и второго d(B|A) признака.