2.11. Побудова функції парної регресії
за допомогою Excel
За допомогою вбудованих функцій можна обчислюватися параметри деяких рівнянь регресії.
Вбудована статистична функція
ЛИНЕЙН
визначає параметри лінійного рівняння
регресії:
.
Порядок обчислення такий.
Вводимо вихідні дані на ЛИСТ 1.
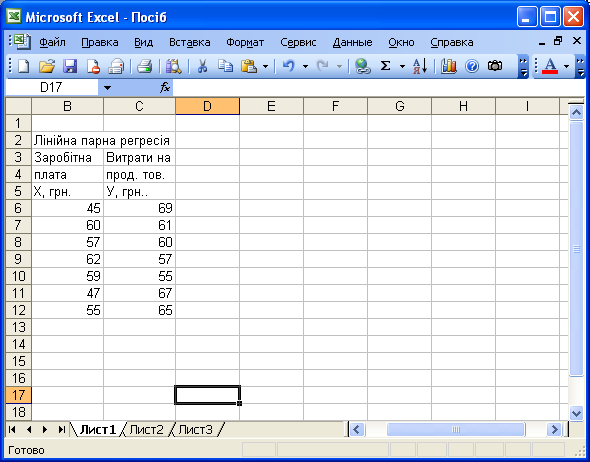
Рис. 2.11.1. – Вихідні дані
Виділимо область вільних клітин 5 2 (5 рядків і 2 колонки), якщо будуть виводитися результати регресійної статистики, або область 1 2 – для отримання тільки коефіцієнтів регресії.
Активізуємо МАСТЕР ФУНКЦИЙ: в головному меню вибираємо ВСТАВКА, а потім ФУНКЦИЯ.
У вікні КАТЕГОРИЯ (рис. 2.11.2) вибираємо СТАТИСТИЧЕСКИЕ, в вікні ФУНКЦИЯ – ЛИНЕЙН натиснути на кнопку ОК.
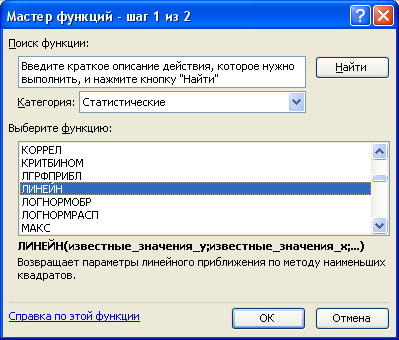
Рис. 2.11.2. – Діалогове вікно “МАСТЕР функций”
Заповнюємо вікно “Аргументы функции” (рис. 2.11.3)
Известные значения – вказуємо діапазон клітин із значеннями ;
Известные значения – діапазон клітин із значеннями ;
Константа – логічне значення, яке вказує на наявність чи відсутність вільного члена в рівнянні. Якщо Константа =1, то вільний член розраховується звичайним чином, якщо Константа=0, то вільний член дорівнює нулю.
Статистика – логічне значення, яке вказує, виводити додаткову інформацію з регресійного аналізу, чи ні. Якщо Статистика =1, то додаткова інформація виводиться, якщо Статистика =0, то виводиться тільки значення оцінок параметрів регресії. Натиснути на кнопку ОК.
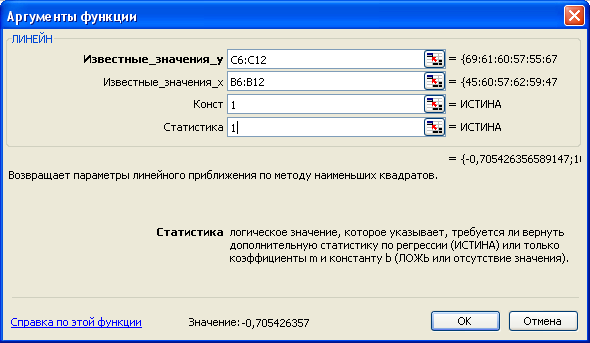
Рис. 2.11.3. – Діалогове вікно вводу аргументів функції линейн
В лівій верхній клітині виділеної області з’явиться перший елемент підсумкової таблиці обчислених значень. Для того щоб розкрити всю таблицю необхідно натиснути на клавішу <F2>, а потів на комбінацію клавіш <CTRL> + <SHIFT> + <ENTER>. В результаті заповняться всі клітини. Зміст цих клітин наступний
Значення коефіцієнта
|
Значення коефіцієнта
|
Середнє квадратичне відхилення |
Середнє квадратичне відхилення |
Коефіцієнт детермінації
|
Середнє квадратичне відхилення |
-статистика |
Число ступенів свободи
|
Регресійна сума квадратів |
Залишкова сума квадратів |
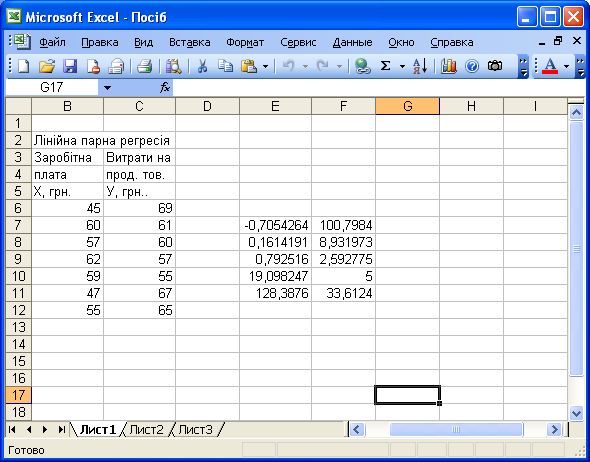
Рис. 2.11.4. – Результат обчислення функції линейн
Таким чином, отримали лінійне рівняння парної регресії
.
Коефіцієнт детермінації
.
Для обчислення параметрів
експоненційної кривої
в Excel використовуються статистична
функція ЛГРФПРИБЛ.
Порядок обчислення аналогічний, як в
ЛИНЕЙН.
2.12. Побудова графіку функції
парної регресії за допомогою Excel
Побудова графіків функцій парної регресії , а також самих функцій здійснюється з допомогою Мастера диаграмм.
Порядок побудови наступний:
Вводимо вихідні дані.
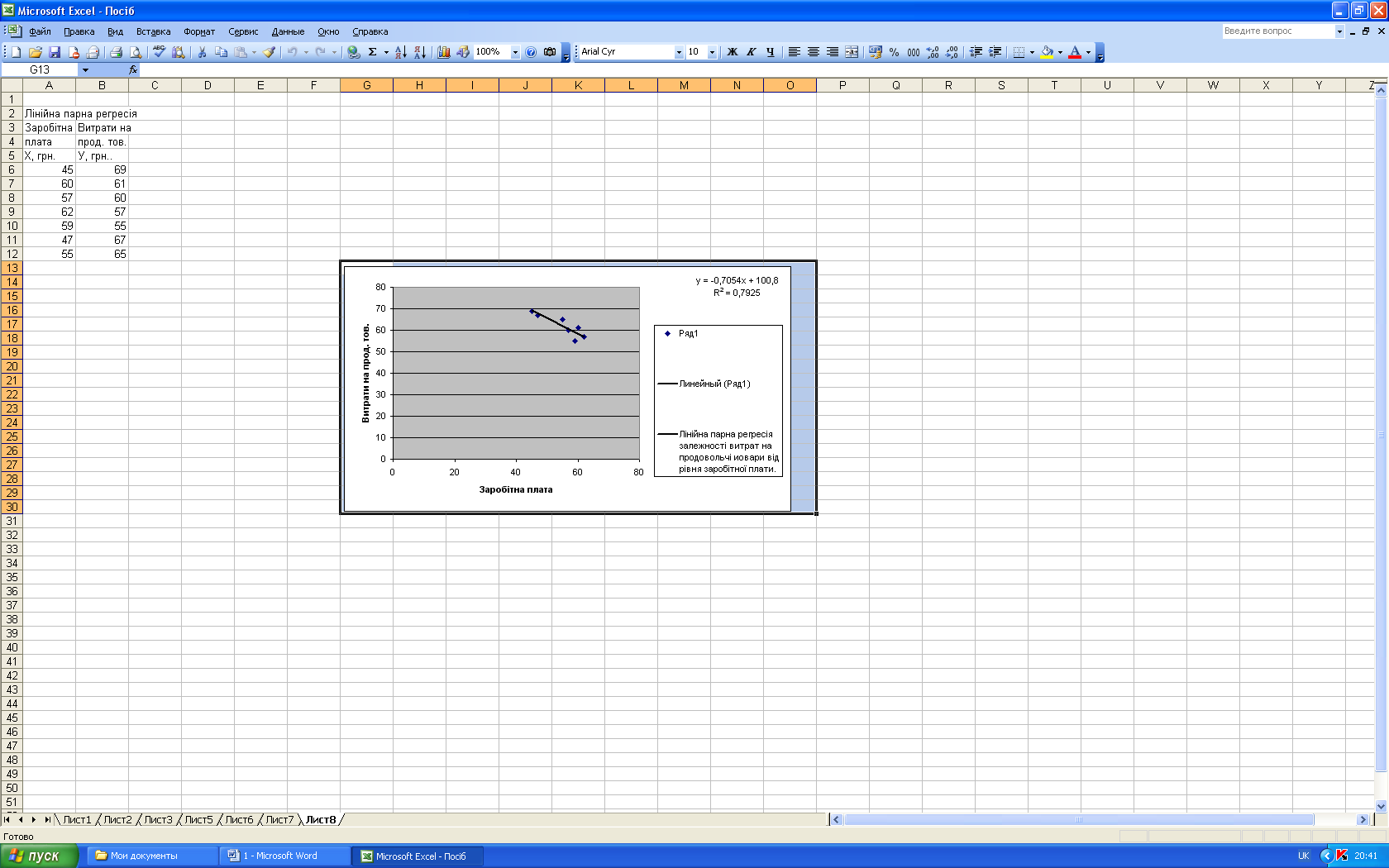
Рис. 2.12.1. – Вихідні дані
Активізуємо Мастер диаграмм одним з двох способів:
в головному меню вибираємо Вставка/Диаграмма;
на панелі інструментів Стандартная клацнути на кнопку Мастер диаграмм.
В вікні Тип вибираємо Точечная (рис. 2.12.2); вид графіку вибираємо в графі рядом зі списком типів. Натиснути на кнопку Далее;
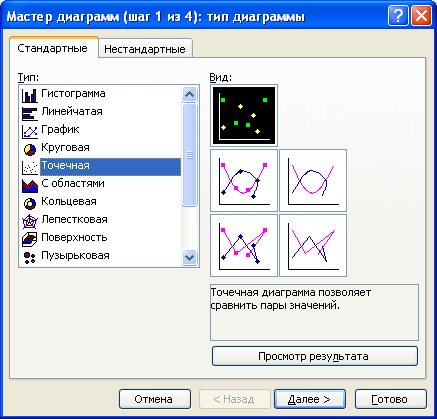
Рис. 2.12.2. – Діалогове вікно Мастер диаграмм: тип диаграммы
Натиснути кнопку Диапазон данных. Вибрати режим в “столбцах” (“строках”). Заповнити діапазон зміни Y, для цього активізуємо Диапазон (встановлюємо стрілку мишки у вікні і натискаємо ліву кнопку), вибираємо клітину В6 і пересуваємося до клітини В12. Натискаємо кнопку Далее (рис.2.12.2.).
Рис. 2.12.3. – Діалогове вікно Мастера диаграмм: исходные данные
Натиснути кнопку Ряд. Заповнити діапазон зміни (див. рис. 2.12.4). Натиснути кнопку Далее.
Рис. 2.12.4. – Діалогове вікно Мастера диаграмм: исходные данные
Заповнюємо параметри діаграм (рис. 2.11.5.): назва діаграми, назви осей, лінії сітки, параметри легенди, і т.д. Натиснути кнопку Далее.
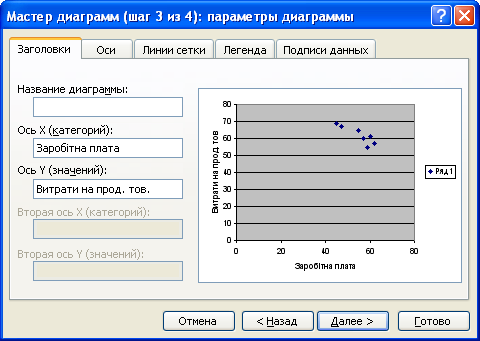
Рис. 2.12.5. – Діалогове вікно Мастера диаграмм: параметри диаграмм
Вказуємо місце розміщення діаграми на окремому або на тому самому листі (рис. 2.11.6.). Натискуємо кнопку Далее.
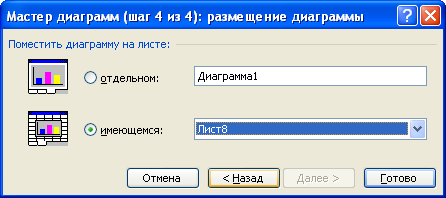
Рис. 2.12.6. – Діалогове вікно Мастера диаграмм: размещение диаграммы
В результаті отримаємо графічне зображення і вихідних даних Рис.2.12.7.).
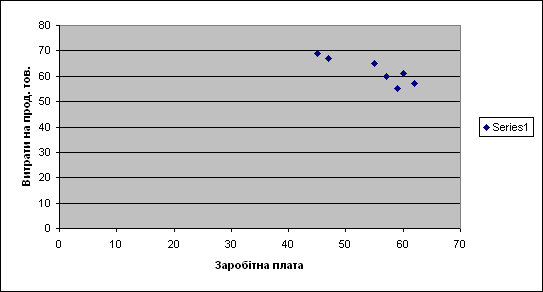
Рис. 2.12.7. – Діаграма: заробітна плата – витрати на продовольчі товари
Ця точкова діаграма представляє собою кореляційне поле. З вигляду даної діаграми можна зробити попередній висновок, що між ознаками і існує лінійна залежність.
Excel дозволяє розмітити на діаграмі лінію регресії. Для цього:
В головному меню вибираємо Диаграмма/ Добавить линию тренда;
В діалоговому вікні вибираємо вид лінії регресії і задаємо, якщо необхідно, відповідні параметри. Якщо ми будуємо поліноміальну лінію регресії, то необхідно задати степінь полінома, для ковзної середньої – кількість точок для яких визначається ковзна середня.
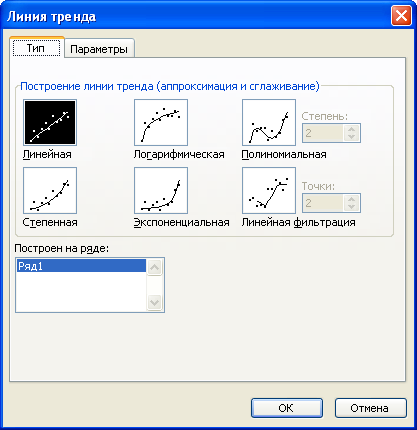
Рис. 2.12.8. – Діалогове вікно типів ліній тренду
На діаграмі крім тренду (лінії регресії) можна відобразити також рівняння регресії і значення коефіцієнта детермінації. Для цього вибираємо відповідні режими на закладці Параметри (рис. 2.12.9); натискуємо кнопку ОК.
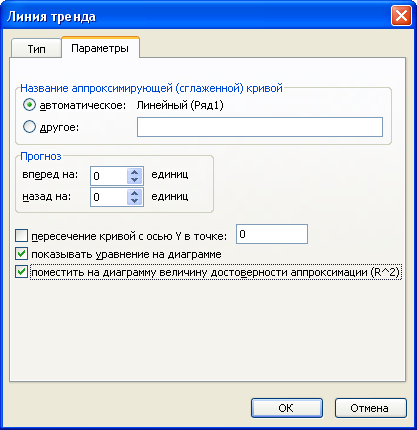
Рис. 2.12.9. – Діалогове вікно параметрів ліній тренду
На рис. 2.12.10 представлено парну лінійну регресію залежності витрат на продовольчі товари від рівня заробітної плати.
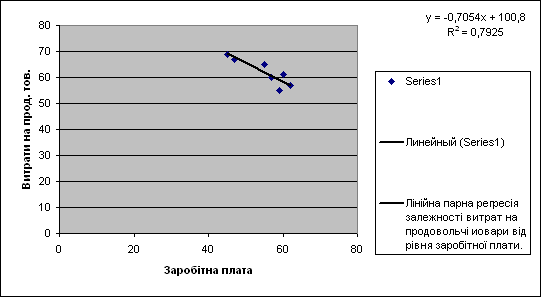
Рис. 2.12.10. – Парна лінійна регресія