Взаимная и автокорреляционные функции сигнала
Корреляционный анализ используется при необходимости оценить временные свойства сигнала без применения спектрального анализа, например, для оценки скорости изменения или длительности сигнала, временной связи (корреляции) одного сигнала с другим.
Взаимная корреляционная функция определяет временную связь двух сигналов во времени. Если сигналы не зависимы друг от друга, их корреляционная функция равна нулю. Чем шире корреляционная функция, тем большая степень связи двух сигналов друг с другом.
Взаимная корреляционная функция определяется соотношением
Пример получения взаимной корреляционной
функции показан на рис.1. Значение
корреляционной функции в любой момент
x определяется площадью пересечения
функций
и
сдвинутой копии
.
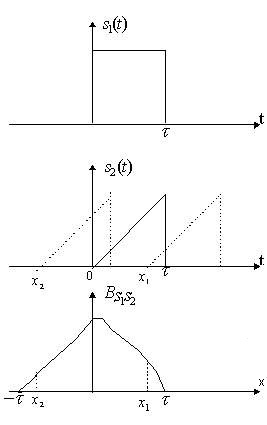
Рис. 1
Взаимная корреляционная функция не обязательно симметрична и её максимум может оказаться не в точке x=0.
Автокорреляционной функцией (АКФ) ограниченного во времени сигнала называется выражение вида
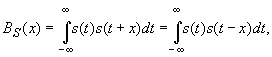
где x – временной сдвиг исходного сигнала.
Геометрический смысл автокорреляционной
функции заключается в определении
площади пересечения функции
и
её копии, сдвинутой на время x (Рис.2)
Рис. 2
Изменяя время сдвига x до тех пор,
пока сигнал и его копия перестанут
пересекаться (в данном случае
),
получим АКФ
.
Очевидно, что при изменении знака сдвига
при одинаковой его величине функция
автокорреляции одинакова, т.е.
,
что говорит о четном её характере. Ясно,
что при x=0 автокорреляционная
функция имеет максимум, при этом
а в свою очередь полная энергия сигнала равна
Таким образом, максимум автокорреляционной функции определяет полную энергию сигнала. При увеличении сдвига x АКФ убывает до нуля.
Связь между автокорреляционной функцией и спектром сигнала
Из свойств преобразований Фурье известно,
что спектр произведения двух сигналов
определяется соотношением свертки:
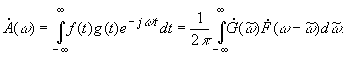
В частном случае при
получается:
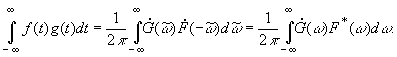
Если положить теперь
,
,
То
,
В этом случае получаем для автокорреляционной функции следующее выражение
Так как
,
то
Величина S2() имеет смысл спектральной плотности энергии сигнала.
При этом прямое преобразование Фурье можно записать в виде:
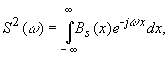
Таким образом, спектральная плотность энергии сигнала связана с автокорреляционной функцией парой преобразований Фурье, что означает однозначную связь ширины частотного спектра и длительности АКФ:
чем шире полоса частот, занимаемая сигналом, тем меньше интервал корреляции, т.е. сдвиг x, в пределах которого корреляционная функция отлична от нуля, и наоборот.
Кроме того, поскольку АКФ не зависит от ФЧХ сигнала, а на форму функции существенно влияет её ФЧХ, то можно сказать, что различным по форме сигналам, обладающим одинаковыми АЧХ и разными ФЧХ, соответствуют одинаковые АКФ.
Акф периодического сигнала
Периодический сигнал на бесконечной оси имеет бесконечную энергию и следовательно, бесконечно большое значение корреляционной функции в нуле. Поэтому для периодических сигналов применяют усредненную периодическую автокорреляционную функцию:
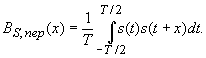
Ясно, что корреляционная функция периодического сигнала имеет тот же период Т.
Пример: гармоническое колебание
.
Его АКФ равна:
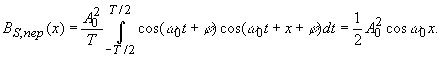
Отсюда видно, что АКФ также является периодической функцией с периодом, равным периоду сигнала.