Комплексный ряд Фурье и спектр сигнала

 

Базисные функции:

, , ;

т.к. , а функции и ортогональны, то и ортогональны.

Квадрат нормы:

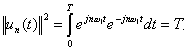
Коэффициенты ряда:

,

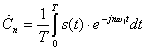так как , то

.

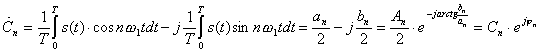Каждая действительная гармоническая составляющая определяется как

.

В комплексном спектре (рис.3.) присутствуют как положительные частоты, так и отрицательные, так как только совокупность составляющих с положительными и отрицательными частотами может дать действительный сигнал.

Рис. 3

Амплитудно-частотный спектр комплексного ряда Фурье является четной функцией, а фазочастотный спектр – нечетной функцией частоты, так как у комплексно-сопряженных чисел модули одинаковы (C_-n=C_n), а фазы отличаются знаком .

Распределение мощности в спектре периодического сигнала

Периодические сигналы определяются средней за период мощностью сигнала:

.

Если сигнал представлен рядом Фурье, то его энергия определяется как сумма средних мощностей каждой гармоники:

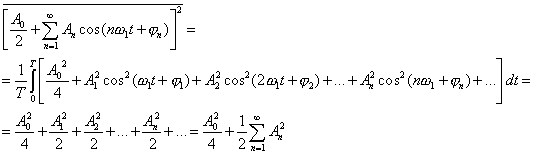
Аналогично получаем для комплексного ряда: .

Равенства и называются равенствами Парсеваля. Синтезированные с помощью ограниченного ряда Фурье сигналы всегда имеют мощность меньшую, чем мощность самого сигнала.

Огибающая спектра периодического сигнала

Линии, соединяющие вершины составляющих АЧС и ФЧС, называются огибающими АЧС и ФЧС. Это непрерывные линии, определяемые не только на частотах гармоник сигнала, но и на любых других (см. рис. 4)

Рис. 4

Выражения для огибающих АЧС и ФЧС получаются из соотношений для комплексных коэффициентов ряда заменой частот на текущую частоту . Так огибающая АЧС тригонометрического ряда определяется из выражений:

;

Огибающая комплексного ряда: 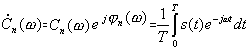, где - огибающая АЧС, а - огибающая ФЧС.

При большом числе составляющих ряда часто бывает удобно для построения спектра сигнала определить и построить огибающие АЧС и ФЧС, а затем отметить отрезки амплитуд и фаз соответствующих составляющих на частотах .

Пример: периодическая последовательность прямоугольных импульсов

Пример: периодическая последовательность прямоугольных импульсов с амплитудой Е, длительностью и периодом Т (рис.5). Отношение называется скважностью последовательности. Такой сигнал не удовлетворяет условиям для функций, к которым применимо разложение в обобщенный ряд Фурье. Однако существующие реальные сигналы, близкие по форме к прямоугольным импульсам, удовлетворяют этим условиям. Поэтому для простоты можно заменить реальные почти прямоугольные импульсы идеализированными прямоугольными, хотя ряд Фурье для них плохо сходится в углах.

Итак, пусть , причем в течение периода сигнал можно описать выражением:

при

Рис. 5

Для упрощения вывода формулы для коэффициентов ряда Фурье, выберем такой интервал интегрирования, на котором сигнал, отличный от нуля расположен симметрично. Обозначим через t₀ время, соответствующее середине импульса на одном из периодов (лучше ближайшем к началу отсчета). Тогда и на периоде имеем

.

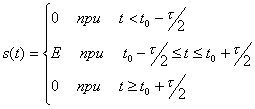Тогда коэффициенты тригонометрического ряда Фурье определятся следующим образом:

;

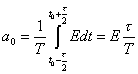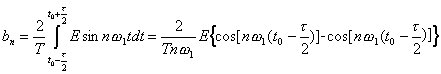
Проведя преобразования, получим:

;

.

Аналогичные результаты гораздо проще получить с помощью коэффициентов для комплексного ряда Фурье. Действительно,

т.к. A_n=2C_n, то .

Соотношения для A_n легко привести к виду, удобному для построения АЧС, помножив и разделив его на , получим:

.

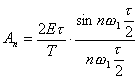Учитывая, что , можно получить и следующее выражение:

.

Так для q=2 («меандр») получаем следующие значения для амплитуд и фаз составляющих спектра:

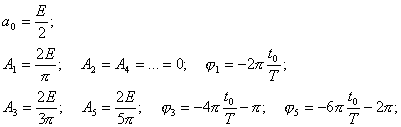
и т.д.

(добавление величины обусловлено переходом синуса через нуль).

Таким образом, спектр меандра имеет вид рис. 6:

Рис. 6

Часто изменение знака синуса отражают на амплитудно-частотном спектре, показывая как бы отрицательное значение амплитуды. Тогда АЧС и ФЧС выглядят следующим образом (рис. 7):

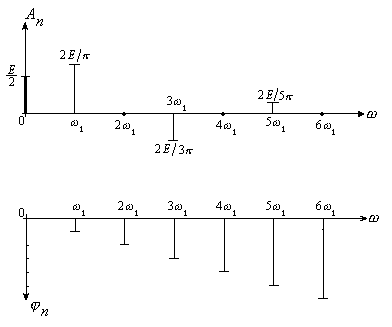
Рис. 7

Если сигнал задан так, что t₀=0, то все , и можно ограничиться только графиком АЧС с «отрицательными» амплитудами.

При увеличении скважности за счет, например, увеличения периода при неизменном , амплитуды составляющих уменьшаются, расстояние между ними также уменьшается.

При произвольных значениях q и t₀ удобнее воспользоваться построением огибающих АЧХ и ФЧХ. Заменим на текущее значение частоты . Получим

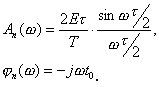
Построим график . Из соотношения для A_n видим, что огибающая меняет знак и, следовательно, проходит через нуль в точках, где , откуда определяем частоты прохождения огибающей АЧХ через нуль:

, где к=1, 2, 3, …

Частота, соответствующая k=1, называется первым нулем спектра. Если , то частота первого нуля равна , а если , то . Следующие нули огибающей спектра кратны этой величине. На частоте огибающая имеет максимум равный

,

откуда постоянная составляющая

.

Следующий максимум будет на частоте .

Величина огибающей на этой частоте равна

;

то есть второй максимум примерно в 5 раз ниже максимума на нулевой частоте. Следующие максимумы уменьшаются пропорционально частоте.

Огибающая ФЧХ линейна и зависит от величины запаздывания или опережения середины импульса относительно t=0, т.е. .

Таким образом, графики огибающих можно нарисовать так, как пунктиром показано на рис.8.

Рис. 8

Для построения самого спектра (АЧС и ФЧС) достаточно на частотах, кратных , провести отрезки до пересечения с огибающей. Для меандра (q=2) в каждом лепестке огибающей (между нулями) будет лишь по одной ненулевой составляющей на частотах: и т.д. Постоянная составляющая . Все четные гармоники имеют в этом случае нулевые амплитуды. Можно амплитудный спектр построить без учета знака синуса во втором, четвертом и т.д. лепестках, в этом случае на этих частотах к следует добавить .

Пара преобразований Фурье. Спектральная плотность сигнала

Пусть сигнал s(t) задан в виде непериодической функции, причем он существует только на интервале (t₁ ,t₂) (пример - одиночный импульс). Выберем произвольный отрезок времени T, включающий в себя интервал (t₁ ,t₂) (см. рис.1).

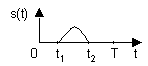
Рис. 1

Обозначим периодический сигнал, полученный из s(t), в виде s_T(t). Тогда для него можно записать ряд Фурье

где

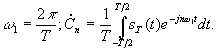
Подставим выражение для в ряд:

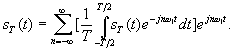
Для того, чтобы перейти к функции s(t) следует в выражении s_T(t) устремить период к бесконечности. При этом число гармонических составляющих с частотами  =n2 /T будет бесконечно велико, расстояние между ними будет стремиться к нулю ( к бесконечно малой величине: , амплитуды составляющих также будут бесконечно малы. Поэтому говорить о спектре такого сигнала уже нельзя, т.к. спектр становится сплошным.

При предельном переходе в случае Т , имеем:

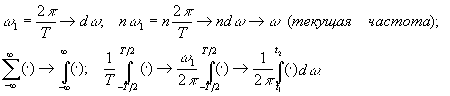
Таким образом, в пределе получаем

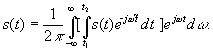
Внутренний интеграл является функцией частоты. Его называют спектральной плотностью сигнала, или частотной характеристикой сигнала и обозначают ,

т.е.

(*)

Пределы интегрирования можно для общности поставить бесконечными, так как все равно там, где s(t) равна нулю, и интеграл равен нулю.

Выражение для спектральной плотности называют прямым преобразованием Фурье. Обратное преобразование Фурье определяет временную функцию сигнала по его спектральной плотности:

(**)

рямое (*) и обратное (**) преобразования Фурье вместе называют парой преобразований Фурье. Модуль спектральной плотности определяет амплитудно-частотную характеристику (АЧХ) сигнала, а ее аргумент называют фазо-частотной характеристикой (ФЧХ) сигнала. АЧХ сигнала является четной функцией, а ФЧХ - нечетной.

Смысл модуля S() определяется как амплитуда сигнала (тока или напряжения), приходящаяся на 1 Гц в бесконечно узкой полосе частот, которая включает в себя рассматриваемую частоту  . Его размерность - [сигнал/частота].