Колебательные цепи при импульсном воздействии
Определим сначала переходную характеристику последовательного колебательного контура (рис. 7), решив дифференциальное уравнение при единичном ступенчатом воздействии:
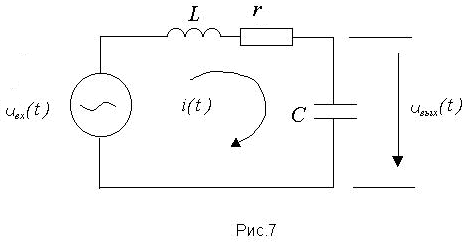
В соответствии с законами Ома и Кирхгофа
имеем для
:
Откуда
Так как
то
или
Обозначим:
В результате имеем дифференциальное уравнение
Решение однородного уравнения определяется
корнями характеристического полинома
которые
равны
Рассмотрим случай высокодобротного контура, у которого
oткуда
.
Таким образом корни характеристического
полинома можно принять равными
.
В этом случае свободная составляющая
напряжения на емкости может быть записана
в виде:
где A и - постоянные интегрирования.
Вынужденное решение, определяемое видом правой части, должно иметь вид:
причем величину В определим путем подстановки вынужденного решения в дифференциальное уравнение.
Т.к.
то
получаем В=1.
Таким образом, полное решение равно
+1.
Величины А и определим из начальных условий, которые в данном случае являются нулевыми, т.е.
Подставляя начальные условия в решение, получаем
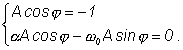
Учитывая, что
,
имеем
Таким образом, для высокодобротного контура переходная характеристика равна
а импульсную определим как производную от переходной , т.е.
На рис.8 показаны графики
и
.
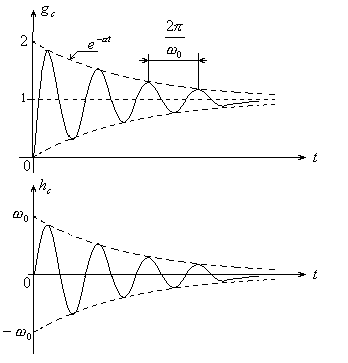
Рис. 8
Чем меньше ,
тем медленнее затухают колебания в
контуре, вызванные единичным или
импульсным воздействием. Если теперь
к контуру приложить напряжение в виде
некоего импульсного сигнала, то отклик,
определяемый интегралом наложения,
будет иметь колебательный характер.
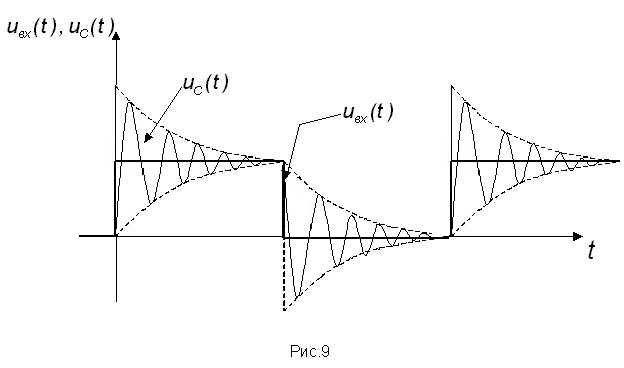
Рассмотрим случай воздействия в виде
последовательности прямоугольных
импульсов длительностью
и периодом Т. Если
и Т значительно превышают время
переходного процесса, равное примерно
,
получим на выходе сигнал , показанный
на рис.9.
Если
,
т.е. период импульсов совпадает с периодом
переходной характеристики, на выходе
цепи получим практически гармонический
сигнал, т.к. за время импульсов и пауз
между ними переходная характеристика
успевает пройти один период колебаний.
Этот случай проще рассматривать частотным
методом: контур подавляет все гармонические
составляющие, кроме первой, поэтому на
выходе получится гармонический сигнал.
Если период кратен периоду колебаний
переходной (импульсной) характеристики
то
при очень высокой добротности на выходе
можно получить гармонический сигнал
на частоте
Сущность операторного метода
Рассмотренные частотный и временной методы объединяются операторным методом, базирующемся на представлении входных и выходных сигналов их преобразованиями Лапласа. Преобразование Лапласа позволяет путем стандартных процедур находить решения линейных дифференциальных уравнений с постоянными коэффициентами, описывающими цепь.
Поиск выходного сигнала осуществляется следующим образом:
а) определяется операторная передаточная характеристика цепи H(p);
б) по временной функции входного сигнала определяется его изображение по Лапласу:
в) определяется изображение выходного сигнала
г) по изображению выходного сигнала определяется оригинал, т.е. временная функция выходного сигнала
Чаще всего изображение выходного сигнала представляет собой отношение двух многочленов по степеням комплексной частоты p , причем степень числителя меньше или равна степени знаменателя :
Если корни знаменателя
простые,
то оригинал определяется с помощью
разложения функции
на элементарные дроби:
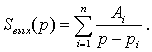
Каждому слагаемому
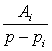соответствует
оригинал
,
а сами коэффициенты определяются
вычетами в полюсах
.
Таким образом, в этом случае
Правила определения оригиналов по
заданной функции
даются
в разделе ТФКП курса «Математический
анализ».