Обоснование частотного метода

Пусть имеется линейный четырехполюсник, на входе которого действует периодический сигнал u_вх (t) произвольной формы с периодом T. Сам четырехполюсник (рис.1) имеет частотную передаточную характеристику

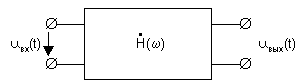
Рис. 1

Требуется с помощью частотного метода определить сигнал на выходе четырехполюсника u_вых (t).

Прежде всего определим спектр входного сигнала: где - коэффициенты ряда Фурье,  ₁=2 /T:

При этом

Каждая составляющая входного сигнала на частоте n₁ имеет вид:

При прохождении через линейную цепь амплитуда и фаза этой составляющей изменяется в соответствии с модулем и фазой частотной передаточной характеристики на этой частоте, т.е.

Произведение коэффициента ряда Фурье входного сигнала на значение частотной передаточной характеристики определяет коэффициенты ряда Фурье для выходного сигнала, т.е.

Этот переход от спектра входного сигнала к спектру выходного справедлив для всех составляющих входного сигнала; таким образом, можно записать

где амплитуда каждой составляющей на выходе определяется произведением модулей амплитуды данной составляющей входного сигнала и АЧХ цепи на частоте составляющей, а фаза равна сумме фазы входной составляющей и ФЧХ на ее частоте.

Пусть на входе действует непериодический сигнал. Тогда сначала определяется его спектральная плотность

Сам сигнал определяется формулой обратного преобразования Фурье:

Из спектральной плотности выделим составляющую на частоте  с амплитудой При прохождении через четырехполюсник составляющая на данной частоте будет иметь амплитуду

После суммирования (интегрирования) по всем составляющим получим

Здесь произведение определяет спектральную плотность выходного сигнала, т.е.

Взятие обратного преобразования Фурье от спектральной плотности выходного сигнала позволяет определить вид временной функции выходного сигнала

Чаcтотные фильтры. Классификация и основные параметры

На практике часто встечаются с необходимостью пропускать или задерживать колебания в заданной полосе частот. Эта задача решается с помощью электрических частотных фильтров, представляющих собой пассивные или активные (с усилителем) линейные четырехполюсники с заданной частотной передаточной характеристикой.

Электрические фильтры могут быть классифицированы по различным признакам: пропускаемым частотам, схемам соединения элементов, типам элементов, характеристикам.

В зависимости от полосы пропускаемых частот различают фильтры нижних частот (ФНЧ), фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ), режекторные (заградительные) фильтры (РФ).

АЧХ идеальных фильтров указанных типов показаны на рис. 2. ФЧХ идеальных фильтров в полосе пропускания (заграждения в РФ) линейная.

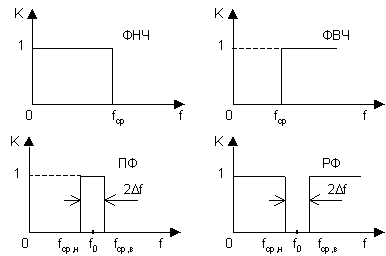
Рис. 2

Полоса пропускания (заграждения в РФ) ограничена у ФНЧ частотами f=0 и f=f_СР - частотой среза, у ФВЧ - f_СР и f= , у ПФ и РФ нижней и верхней частотами среза. Часто ПФ и РФ характеризуются средней частотой f₀ и полной полосой пропускания (заграждения) 2 f.

В зависимости от схемы различают фильтры из Г-образных ( рис. 3, а), Т-образных (рис. 3, б) и П-образных звеньев (рис. 3, в).

          а)                                              б)                                               в)

Рис. 3

По числу звеньев различают фильтры однозвенные (простейшие) и многозвенные. Звенья содержат последовательные и параллельные ветви. Простейшим является Г-образное звено, которое содержит два сопротивления. Особенностью такого звена является невозможность сделать равными (симметричными) сопротивления фильтров со стороны входных (1-1) и выходных (2-2) клемм. Чаще применяют симметричные Т- и П-образные звенья. Они создаются последовательным соединением двух Г-образных звеньев. У Т-образного звена, как правило, ; у П-образного - .

В простейших реактивных фильтрах сопротивления и Г-образного звена подбираются так, чтобы произведение их на любой частоте было бы постоянным. Этого можно добиться, если ветви фильтра содержат реактивности разных знаков, т.е. одна ветвь содержит индуктивность, другая - емкость. Тогда

Такие фильтры называются фильтрами типа "k". Более сложные типы фильтров, включающие в ветви последовательные или параллельные контура, называются фильтрами типа "m".

В случаях, когда частота среза не превышает нескольких килогерц, находят широкое применение RC-фильтры.

Различают пассивные и активные RC-фильтры. В активных RC-фильтрах используют усилитель с большим коэффициентом усиления (чаще операционный усилитель в микросхемном исполнении), который охвачен частотно-зависимой (RC-цепь) отрицательной обратной связью. Наличие усилителя позволяет использовать многозвенные фильтры в цепи обратной связи без сильного ослабления сигнала в полосе пропускания.

К основным характеристикам фильтра наряду с частотным коэффициентом передачи относят частотную характеристику затухания, которая определяется как

дБ.

Эта характеристика определяет степень уменьшения амплитуды выходного сигнала по сравнению с входным. Если K=1, то а=0дБ, если K=0, то а= . Таким образом, характеристики затухания идеальных фильтров имеют вид, показанный на рис. 4.

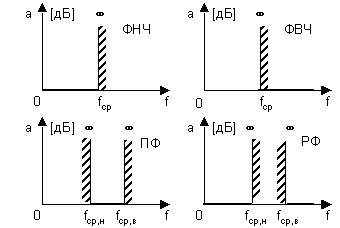
Рис. 4

Из параметров фильтра отметим характеристическое сопротивление фильтра, которое для успешной передачи энергии через фильтр в нагрузку должно быть активным и равно сопротивлению нагрузки (согласованный фильтр).

Для создания реальных фильтров с характеристиками, близкими к идеальным, элементы не должны содержать потерь; так для ФНЧ Г-образного вида сопротивление должно быть бесконечно большим во всей полосе задерживания, а сопротивление - бесконечно малым, и, наконец, фильтр должен быть согласованным на всех частотах. Эти условия практически выполнить невозможно. Поэтому характеристики реальных фильтров всегда отличаются от идеальных. Прежде всего имеет место плавный переход от полосы пропускания к полосе задерживания, что не позволяет указать точное значение частоты среза. Поэтому при проектировании фильтров задаются полосами эффективно пропускаемых и эффективно задерживаемых частот (см. рис. 5, а, б).

а)                               б)

Рис. 5

В полосе эффективно пропускаемых частот ( 0, f₁ ) затухание не должно быть больше некоторого заданного значения а₁ (обычно а₁ составляет 3-6 дБ, что соответствует K₁=0,86-0,707). В полосе эффективного задерживания ( f₂, ) затухание фильтра должно быть больше заданного значения а₂. Область частот ( f₁, f₂ ) называют полосой перехода. Чем, быстрее изменяется затухание внутри этой области, тем она уже. Скорость изменения K(f) или a(f) внутри полосы перехода характеризуют в децибеллах на октаву (полоса удвоения частоты), или в децибеллах на декаду (полоса удесятерения частоты).

В зависимости от вида используемых элементов различают фильтры, содержащие индуктивности и емкости - реактивные фильтры, емкости и активные сопротивления - безиндуктивные или RC-фильтры, фильтры, состоящие из кварцевых пластин (резонаторов) - пьезоэлектрические фильтры.

Простейшие фильтры первого порядка

К простейшим фильтрам первого порядка относятся цепочки, содержащие активные сопротивления и один реактивный элемент: емкость или индуктивность, включенные последовательно или параллельно. На рис.6 изображены возможные включения элементов R и L, R и C.

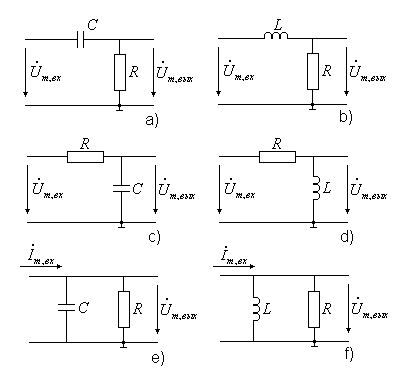
Рис. 6

Цепочки вида a), b), c), d) питаются от источника напряжения, а цепочки вида e) и f) – от источника тока.

Для определения фильтрующих свойств этих цепочек, запишем для каждой из них частотный коэффициент передачи, причем для цепочек a), b), c), d)

,

а для цепочек e), f)

,

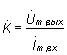, – комплексные амплитуды входных напряжений и тока, -комплексная амплитуда выходного напряжения. Коэффициенты передачи определим для случая холостого хода на выходе ( ).

Для определения коэффициентов передачи цепочек воспользуемся комплексным методом, при котором гармонические токи и напряжения представляем их комплексными амплитудами ( ), емкость и индуктивность их комплексными сопротивлениями:

.

Покажем вывод коэффициента передачи на примере цепочки вида а).

Ток, протекающий в цепи в соответствии с 2-м законом Кирхгофа и законом Ома равен

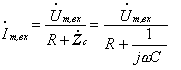
в свою очередь выходное напряжение равно

,

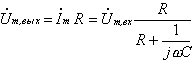Откуда получаем следующее выражение для частотного коэффициента передачи этой цепочки:

;

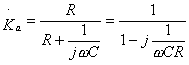Аналогично легко вывести и коэффициенты передачи для других цепочек

;

;

;

;

.

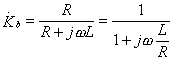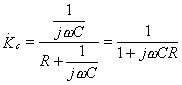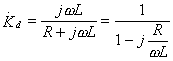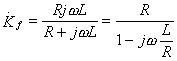Обозначим : RC= _ц, L/R= _ц, где  _ц - постоянная времени цепи, = , где - граничная частота цепочки.

Получаем для цепочек a) и d) коэффициент передачи вида:

для цепочек b) и c):

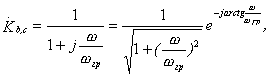
и для цепочек e) и f) соответственно :

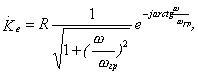
Сравнивая соотношения для коэффициентов передачи всех цепочек, можно заметить, что все цепочки можно разделить на 2 вида, коэффициенты передачи которых можно записать следующим образом:

причем в последовательных цепочках , а в параллельных ,

Для построения графиков АЧХ и ФЧХ и оценки фильтрующих свойств цепочек первого порядка рассмотрим следующие области частот: область низких частот , область высоких частот и .

Для первого типа цепочек имеем:

В области низких частот поэтому

Таким образом, в области низких частот для первого типа цепочек (a, d, f) АЧХ линейно возрастает от нуля, т.е. наклон АЧХ здесь составляет 6 дб/октаву: увеличение в 2 раза частоты увеличивает в 2 раза модуль коэффициента передачи, а ФЧХ примерно равна  /2.

На частоте модуль коэффициента передачи

Отсюда и название этой частоты –“граничная”; эта частота определяет полосу пропускания фильтра по уровню K₀/2.

В области высоких частот

т.е. в области высоких частот цепочки первого типа имеют равномерную АЧХ, равную K₀ ; а у цепочки второго типа модуль АЧХ с увеличеним частоты изменяется по закону , т.е. имеет наклон -6 дб/октаву, ФЧХ в этой области примерно равна - /2. На рис.7 представлены графики АЧХ и ФЧХ обоих типов цепочек.

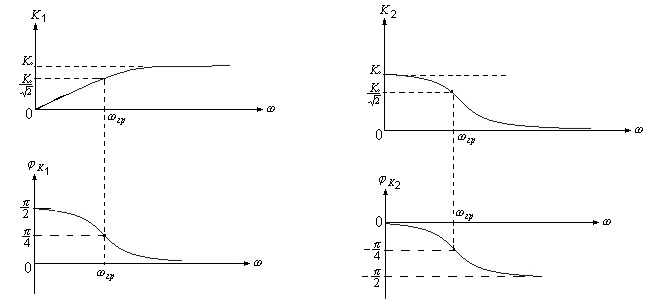
Рис. 7

Таким образом, простейшие апериодические цепочки порядка первого типа (вида a, d, f рис.6) являются фильтрами высокой частоты со спадом частоты АЧХ вне полосы пропускания ( , ) 6 дб/октаву; простейшие цепочки второго типа (b, c, e) являются фильтрами низких частот со спадом АЧХ вне полосы пропускания (0, ) также в 6 дб/октаву. Граничная частота здесь определяется по уровню пропускания половинной мощности или по спаду АЧХ на 3 дб от максимума.

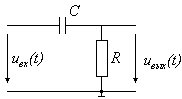
Простейшие дифференцирующие и интегрирующие цепи В радиоэлектронике часто возникает необходимость в построении цепей, сигнал на выходе которых пропорционален производной или интегралу от входного воздействия. Обычно эти задачи решаются приближенно при помощи электрических схем при некоторых условиях, накладываемых на сигнал. Рассмотрим схему, состоящую из последовательно соединенных емкости и активного сопротивления (рис. 8): Рис .8 Запишем для нее дифференциальное уравнение, связывающее входное и выходное напряжение. Так как ток через емкость равен и в соответствии с законами Кирхгофа и Ома , то откуда получаем При условии (1) имеем приближенное равенство (1') т.е. схема в этом случае приближенно выполняет операцию дифференцирования. Если же имеет место противоположное неравенство, т.е. (2) то получаем приближенное равенство вида (2') т.е. цепочка в этом случае приближенно повторяет сигнал. Условие (1) характеризует медленное изменение напряжения, а условие (2) – быстрое, т.е схема рис.3 хорошо дифференцирует медленные функции, плохо быстрые. Из выражения (1) видно, что условие лучше выполняется при малой величине произведения CR, называемой постоянной времени. Однако о скорости изменения функции лучше судить по ее спектральному составу: чем выше максимальная частота спектра, тем больше скорость изменения сигнала. Как было показано раньше, операции дифференцирования сигнала во временной области соответствует в частотной области умножение спектра входного сигнала на величину ј . Т.е. идеально дифференцирующая цепь должна иметь частотный коэффициент передачи вида: где а –постоянный множитель с размерностью [1/ ]. Как было показано выше, частотный коэффициент передачи цепочки рис.8 равен и при =1/RC (3) получаем приближенное равенство, соответствующее идеальному дифференциатору: , (3') (a= ) Отсюда, условие хорошего дифференцирования сигнала данной цепочкой выражается формулой (3) вместо (1), т.е. для синусоидального колебания с частотой  дифференцирование осуществляется при условии, что частота его много меньше величины 1/RC. Если на входе действует сложный сигнал, то он будет хорошо дифференцироваться, если наивысшая частота в спектре входного сигнала много меньше граничной частоты цепочки. 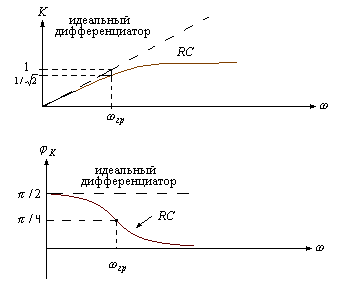На рис.9 показаны АЧХ и ФЧХ идеального дифференциатора и цепочки вида рис.8 Рис. 9 Если теперь выходное напряжение снимать с емкости (т.е. ), то дифференциальное уравнение будет иметь вид: При выполнении условия (1) получаем а при выполнении условия (2), получим откуда имеем (4) т.е. в этом случае получаем на выходе сигнал, пропорциональный интегралу от входного, следовательно, цепочка (рис.10) является интегрирующей. Данная цепочка будет хорошо интегрировать быстро меняющиеся сигналы и плохо – медленные. Рис. 10 При этом интегрирование выполняется тем лучше, чем больше постоянная времени цепи. В частотной области операция дифференцирования сводится к делению спектра входного сигнала на j . Т.е. частотный коэффициент передачи идеального интегратора должен иметь вид где b постоянный коэффициент с размерностью [ ]. Для схемы рис.10 частотный коэффициент передачи равен При выполнении условия = 1/RC , получаем приближенное равенство, соответствующее идеальному интегратору: (b= ) . 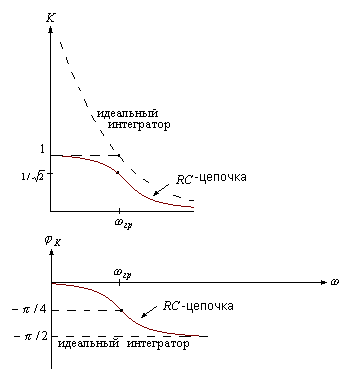(4') АЧХ и ФЧХ идеального интегратора и цепочки вида рис.10 показаны на рис. 11 Рис. 11

Простейшие фильтры второго порядка

К простешим фильтрам второго порядка относят цепочки, содержащие две реактивности разного знака: индуктивность и емкость. В зависимости от схемы включения контура к источнику сигнала различают последовательный и параллельный колебательный контуры. В последовательном контуре источник сигнала и элементы контура (обычно это конденсаторы и катушки индуктивности) соединены последовательно. Выходное напряжение чаще снимают с конденсатора (см. рис.12).

Рис. 12

Моделью конденсатора является емкость С, катушку индуктивности обычно представляют последовательным соединением индуктивности L и активного сопротивления , отражающего сопротивление провода катушки постоянному току. На схеме рис.12 источник сигнала представлен источником ЭДС e(t) с внутренним сопротивлением .

В параллельном контуре источник сигнала представляют в виде источника тока, параллельно с которым соединены емкость и катушка индуктивности (рис.13).

Рис. 13

Частотный коэффициент передачи определяется при гармоническом сигнале на входе. Определим собственные параметры контуров (при R_c =0 для источника ЭДС и R_c = для источника тока в режиме холостого хода на выходе).

Для последовательного контура, используя комплексный метод, получаем

.

(1)

Для параллельного контура коэффициентом передачи является сопротивление контура, т.к.

(2)

В обоих случаях знаменатель определяется полным последовательным сопротивлением контура

.

На частоте, называемой резонансной, мнимая часть последовательного сопротивления равна нулю, т.е. , откуда получаем известное соотношение (формула Томпсона) .

Величины определяют волновое или характеристическое сопротивление контура, т.е. сопротивление реактивных элементов на резонансной частоте.

Таким образом, на резонансной частоте .

Отношение волнового сопротивления последовательного контура к сопротивлению потерь катушки называют собственной добротностью контура

.

(3)

Соотношения (1) и (2) с учетом введенных обозначений легко преобразуются к виду

,   ,

(4) (5)

где приближенное равенство справедливо для Q>1.

Коэффициент передачи последовательного контура на резонансной частоте равен добротности, т.е. амплитуда выходного напряжения в Q раз больше амплитуды входного. Собственное сопротивление же последовательного контура на резонансной частоте действительно и равно и увеличивается по модулю с изменением частоты влево или вправо от резонансной.

Коэффициент передачи параллельного контура (а, следовательно, и его полное сопротивление) на резонансной частоте максимальны и равны:

.

С изменением частоты модуль полного сопротивления уменьшается.

При определении характера поведения АЧХ и ФЧХ цепей вблизи резонанса( ) преобразуем выражение под корнем с учетом следующих обозначений:

,

,

где – абсолютная расстройка частоты сигнала относительно резонансной частоты, - относительная расстройка;

,

(6)

где величина называется обобщенной расстройкой. Тогда вблизи резонанса можно записать

; .

(7) (8)

На частотах, соответствующих = 1, коэффициенты передачи в раз меньше резонансных. При = 1, имеем , где абсолютная расстройка, соответствующая этому случаю. Величина называется полосой пропускания контура как полосового фильтра. Отсюда получают второе определение добротности контура в виде отношения резонансной частоты к полосе частот , определяемой на уровне от максимума.

В области низких частот ( )

, .

В области высоких частот ( )

, .

Рис. 14

На рис.14 показаны АЧХ и ФЧХ последовательного (а) и параллельного (б) контуров.

На границах полосы пропускания ФЧХ имеет значение от значения ФЧХ на резонансной частоте ( ).

С увеличением добротности полоса пропускания уменьшается (избирательность увеличивается), наклон ФЧХ в полосе пропускания увеличивается.

Легко показать, что конечные значения сопротивления источника сигнала и нагрузки уменьшают добротность системы, расширяя ее полосу пропускания, т.к. при этом увеличивается последовательное сопротивление контура постоянному току. Так как сопротивление в схеме последовательного контура просто складывается с , то добротность оказывается равной . Для определения влияния и в параллельном контуре заменим последовательную модель катушки индуктивности на параллельную (см. рис.15).

Рис. 15

Величины и выразим из равенства:

.

Преобразуем правую часть в обычную алгебраическую форму комплексного числа, избавившись от комплексности в знаменателе:

.

Вблизи резонансной частоты величина , следовательно

,

(9)

откуда .

Кроме того, при Q>1 можно считать, что , поэтому

,

следовательно, .

Собственная добротность контура в схеме рис.15, б определяется как

.

При учете сопротивлений и общее активное сопротивление контура равно меньше сопротивления , следовательно, добротность меньше собственной добротности контура.

Резонансное сопротивление параллельного контура в этом случае определяется как , и, таким образом, меньше самого меньшего из сопротивлений и . Следовательно, чтобы полностью использовать избирательные свойства контура (заданные полосой ), необходимо на входе использовать источник сигнала с большим выходным сопротивлением , и подключать нагрузку с .

При анализе схем с параллельными контурами можно источник тока с большим заменить источником ЭДС с большим (рис.16).

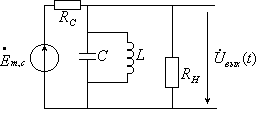
Рис. 16

При характеристики такой схемы будут определяться собственными параметрами контура. В этом случае в контур втекает ток 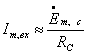. На резонансной частоте

,

Откуда коэффициент передачи на резонансной частоте по напряжению

.

Поведение же АЧХ и ФЧХ этого коэффициента передачи будет аналогично рассмотренному выше поведению АЧХ и ФЧХ сопротивления параллельного контура с добротностью

  .

Сопротивления и можно с помощью формулы (9) пересчитать в последовательные, которые называют вносимыми сопротивлениями:

; ,

откуда ясен смысл уменьшения добротности при и .

При невозможности выполнить эти требования используют так называемое частичное (неполное) включение контура.

Разновидности схем таких контуров приведены на рис.17.

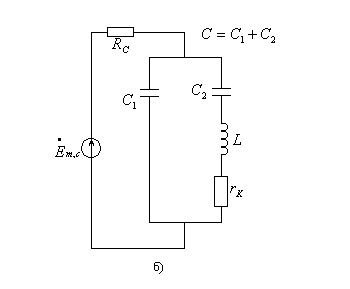
Рис. 17

Схема рис.17,а называется параллельным контуром второго вида, а рис.17,б – параллельным контуром третьего вида. Полное включение, рассмотренное выше, образует контур первого вида.

Коэффициентом включения называют отношение индуктивности (или емкости), к которым подключен источник (или нагрузка), к полной индуктивности (или емкости) контура. Для схемы рис.17,а ; для схемы рис.17,б .

Резонансное сопротивление контуров с неполным включением определяется как . Вносимые сопротивления также уменьшаются в p ² раз. Поэтому полная добротность системы уменьшается меньше, чем при полном включении, а при очень малых практически не уменьшается (правда ценой значительного уменьшения резонансного сопротивления, и, следовательно, выходного напряжения).

На схеме рис.17,в показано подключение источника и нагрузки к контуру так, чтобы ослабить их шунтирующее действие на контур.

Неполное влючение контура используется также для такого согласования с источником и нагрузкой, при котором в нагрузку передается максимальная мощность. Это возможно при выполнении равенств . При этом добротность контура уменьшается в два раза, а полоса вдвое увеличивается.

Одним из недостатков использования схем с неполным включением является дополнительный электротехнический резонанс напряжений, возникающий в ветви, содержащей емкость и индуктивность.

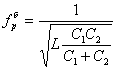Эти последовательные резонансы происходят на частотах, отличных от резонансной частоты всего контура. Так для схемы рис.17,а , а последовательный резонанс возникает на частоте ; для схемы рис.17,б , а .

Подбирая коэффициенты включения, можно менять частоты последовательных резонансов так, чтобы они не влияли на прохождение сигналов.

Прохождение амплитудно-модулированных колебаний через колебательную систему

Пусть в параллельный колебательный контур втекает входной амплитудно-модулированный ток

,

(1)

где M – глубина амплитудной модуляции при управляющем сигнале в виде гармонического колебания с частотой и начальной фазой ; - частота и начальная фаза несущего колебания, . Определим напряжение на выходе контура с резонансной частотой , добротностью Q и резонансным сопротивлением .

Спектр входного тока содержит три гармонические составляющие, амплитуды, фазы и частоты которых легко определяются путем тригонометрических преобразований выражения (1). Имеем

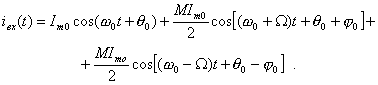
Поскольку контур является линейной цепью, можно рассматривать прохождение через него каждой составляющей отдельно.

Пусть = (точная настройка). Тогда коэффициент передачи (сопротивление) контура на частотах , будут равны соответственно:

где . Величина называется постоянной времени контура. Выходное колебание в соответствии с частотным методом будет иметь вид:

(2)

Сопоставив полученное выражение с (1), видим, что частота и фаза несущей АМ-колебания при прохождении через настроенный на несущую контур не изменяются. Огибающая же имеет на выходе меньший коэффициент глубины модуляции и другую начальную фазу.

Отношение M_вых к M иногда называют коэффициентом демодуляции, причем

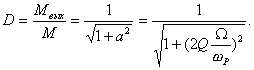
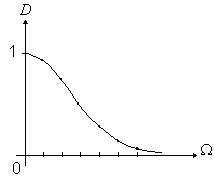
Рис. 18

На рис.18 показан график зависимости от частоты модулирующего сигнала . Практически он соответствует правой ветви АЧХ колебательного контура. Запаздывание по фазе огибающей . Форма огибающей остается прежней (гармонической).

Чем выше частота модуляции , тем больше относительное ослабление амплитуды колебаний боковых составляющих ( ) и, следовательно, меньше глубина модуляции выходного напряжения. Если на входе действует более сложное сообщение, состоящее из нескольких различных частот , то каждой из них будет соответствовать свое ослабление коэффициента глубины модуляции ; следовательно выходное напряжение по форме будет отличаться от входного тока. Таким образом зависимость определяет степень линейных (частотных) искажений огибающей, то есть передаваемого сообщения.

Если полоса частот огибающей не выходит за пределы полосы пропускания, то линейность ФЧХ в пределах этой полосы удовлетворяет условию отсутствия фазовых искажений. Огибающая на выходе будет запаздывать на величину , определяющуюся наклоном ФЧХ в точке , т.е.

.

Таким образом задержка сообщения (огибающей) в одиночном контуре, полоса прозрачности которого достаточна для удовлетворительного пропускания спектра сообщения ( ), равна постоянной времени контура.

Несовпадение частоты несущей и резонансной частоты контура (расстройка) приведет к ассиметрии амплитуд и фаз боковых частот на выходе контура.

АЧХ контура и положение спектра входного тока для этого случая показаны на рис.19.

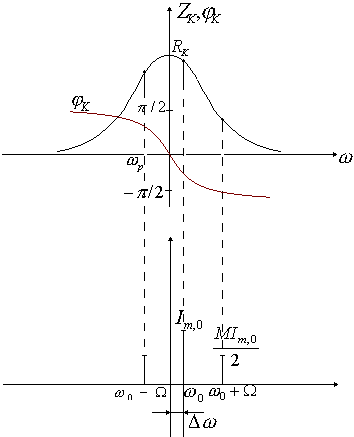
Рис. 19

При нижняя боковая на выходе будет больше по величине, чем верхняя. Фазы их также получат несимметричные приращения. В результате высокочастотное напряжение не будет уже чисто амплитудно-модулированным, огибающая по форме будет отличаться от огибающей тока, кроме того, возникнут медленные изменения частоты несущей (паразитная угловая модуляция).

Из-за изменения в спектре огибающей радиосигнала на выходе амплитудного детектора будет получен отличный от модулирующей функции сигнал.
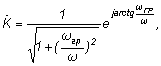
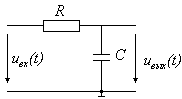
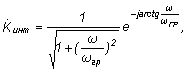
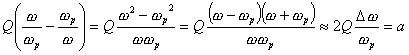
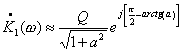