Взаимная заменяемость частоты и времени в паре преобразований Фурье

Если функция s(t) четна относительно t, то ее спектральная плотность является вещественной функцией, т.к. в этом случае

второй интеграл в силу нечетности синуса равен нулю. Для четной функции можно произвольно выбирать знак в экспоненте для прямого и обратного преобразования Фурье, так как и сама функция s(t) и ее спектральная плотность четные относительно оси ординат. Запишем выражение для s(t) через обратное преобразование Фурье, выбрав знак минус в экспоненте

,

и осуществим замену  на t и t на  . Получим

Интеграл в этом выражении можно рассматривать как спектральную плотность S'(  ) новой функции S(t), полученной заменой  на t.

Тогда имеем 2s()=S'(), т.е. спектральная плотность этой новой функции равна 2 , умноженная на спектральную плотность сигнала, полученного в результате замены t на некоторой временной функции s(t).

Таким образом, если четному колебанию s(t) соответствует спектральная плотность S(), то четному колебанию S(t) соответствует спектральная плотность 2s().

В качестве примера рассмотрим сигналы, один из которых имеет вид одиночного прямоугольного импульса (рис. 8а), а второй обладает прямоугольной спектральной плотностью (рис. 8б).

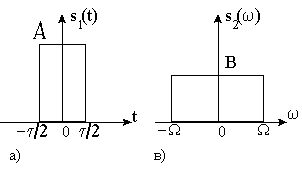
Рис. 8

Сигналу соответствует знакопеременная спектральная плотность , имеющая максимум A  при =0, нули на частотах (см.рис.9а).

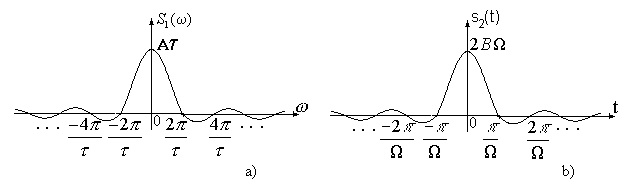
Рис. 9

В соответствии с теоремой взаимности сигналу со спектральной плотностью, показанной на рис.8б, соответствует временная функция , показанная на рис. 9б.

Данное свойство удобно использовать в тех случаях, когда по известной паре преобразований Фурье можно найти временную функцию, спектр которой соответствует временной функции известного сигнала, и наоборот.

Преобразование Лапласа на плоскости комплексной частоты

Тригонометрическая и экспоненциальная формы ряда Фурье представляют вещественный сигнал s(t) в зависимости от действительной частоты  . Преобразование Лапласа - более общий способ описания сигналов, позволяющий значительно упростить анализ прохождения сигналов через линейные цепи, особенно при быстро меняющихся импульсных воздействиях, когда важны переходные процессы.

Преобразование Лапласа использует методы контурного интегрирования на плоскости комплексной частоты р=  +j  , где  и  действительные числа. Это преобразование справедливо и для тех сигналов, для которых интегралы Фурье не сходятся.

Односторонним прямым преобразованием Лапласа для функции s(t), существующей при 0<t< , называется интеграл вида

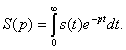
Обратным преобразованием Лапласа является соотношение

Сигнал s(t) называется оригиналом, а его представление по Лапласу или операторная функция называется изображением.

Переход от оригинала к изображению и наоборот принято условно изображать так:

Большим преимуществом преобразования Лапласа является его простая связь с преобразованием Фурье. Для этого необходимо лишь осуществить замену р  j  :

Основные свойства преобразования Лапласа

а) Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т.е. если s(t)=a f(t)+b g(t), то S(p)=a F(p)+b G(p).

Это свойство вытекает из линейности операции преобразования Лапласа.

б) Производная оригинала равна изображению исходного сигнала, умноженного на р, за вычетом значения оригинала в точке t=0, т.е.

в) Изображение интеграла от оригинала равно изображению оригинала, деленного на р, т.е.

Определение оригинала по изображению

Для определения оригинала по изображению самым общим (и самым сложным) методом является взятие интеграла обратного преобразования Лапласа:

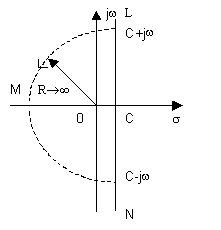
Рис. 1

Величина С>0 в пределах интеграла ограничивает на комплексной плоскости область интегрирования (рис.1). Значение постоянной С определяется характером функции S(p)e^pt : путь интегрирования (на рис.1 он проходит по прямой С-j  , C+j  ) должен проходить правее полюсов этой функции.

Можно вместо прямого пути интегрирования образовать замкнутый контур (пунктир на рис.1) добавлением дуги конечного радиуса, причем величина этого радиуса должна быть такова, чтобы в контуре интегрирования оказались бы все полюса функции S(p). Для функций s(t),определенных для t>0, контур должен быть расположен в левой полуплоскости.

Получение оригинала в этом случае сводится к определению:

где    - сумма вычетов в полюсах функции S(p) .

Вычет определяется следующим образом.

При наличии полюсов изображение всегда можно представить в виде отношения двух полиномов

Полюсами функции S(p) будут корни уравнения W(p)=0, т.е. нули знаменателя.

Если функция S(p) имеет в точке p₁ простой полюс, то

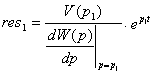
Если полюс p₁ имеет кратность m (m - целое положительное число), то

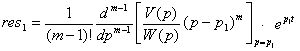
Более простым способом является использование таблиц соответствия оригинал-изображение для некоторых функций. В таблице 1 даны эти соответствия для некоторых часто встречающихся в радиоэлектронике сигналов.

Таблица 1

 

Оригинал (t>0)	Изображение
(t)	1
A
e-  t
1- e-  t
t
te-  t
sin  t
cos t
e- t cos 0t

В справочниках можно найти более полные таблицы. Однако не всегда можно сразу обратиться к таблице. В этом случае можно провести такие алгебраические преобразования изображения, чтобы привести его к табличным функциям.