Линейная комбинация сигналов

Так как преобразование Фурье, определяющее спектр (или спектральную плотность) сигнала, является линейным, то при любой линейной комбинации сигналов спектр (спектральная плотность) результирующего сигнала является той же линейной комбинацией спектров исходных сигналов.

Пусть заданы периодические сигналы и с периодами .

Им соответствуют спектры и с частотами и n, k=0,  1,  2, …

Линейная комбинация

для непериодических сигналов и при имеем:

Для примера использования данного свойства определим спектральную плотность пары прямоугольных импульсов (рис.1а). Представим этот сигнал в виде разности двух одиночных прямоугольных импульсов (рис.1в), спектральная плотность для которых нам уже знакома.

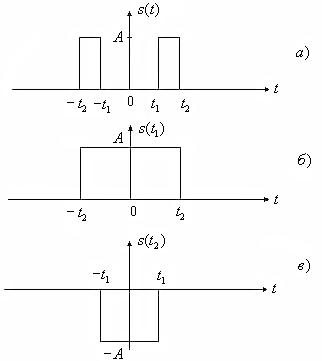
Рис. 1

Для одиночных четных импульсов имеем соответственно

Следовательно, спектральная плотность пары импульсов равна

Графическая интерпретация построения спектральной плотности для этого случая показана на рис.2.

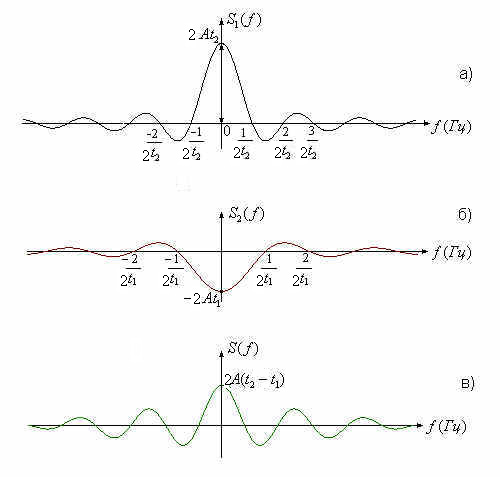
Рис. 2

При задании сигнала в виде четной функции построить результирующую спектральную плотность легко. В более общем случае следует не забывать, что линейной комбинации подвергаются комплексные функции.

При рассмотрении последующих свойств мы ограничимся лишь непериодическими сигналами.

Сдвиг сигнала во времени

Пусть сигнал s₁(t) существует на конечном интервале времени (рис 3.а). Его спектральная плотность равна Аналогичный по форме сигнал отличается лишь положением на оси времени, т.е. причем при второй сигнал отстает от первого (рис 3б) ( - время задержки или запаздывания), при < 0 второй сигнал опережает первый (рис. 3в).

Рис. 3

Спектральная плотность второго сигнала равна

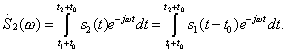
Введем переменную , тогда , dt = dx,

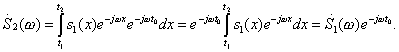
Отсюда видим, что сдвиг во времени сигнала на величину приводит лишь к изменению фазочастотной характеристики сигнала на величину ( ). На рис.4 показаны АЧХ и ФЧХ сигналов и при t

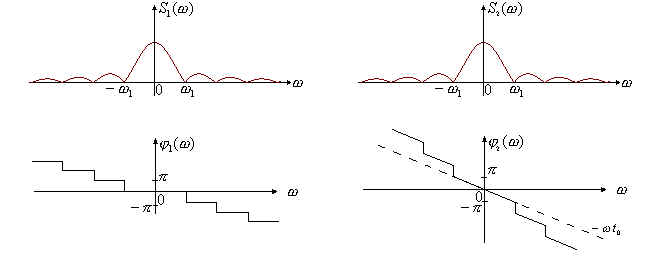
Рис. 4

Очевидно и обратное положение: если всем составляющим спектра функции дать фазовый сдвиг то получим сигнал , сдвинутый по времени на величину .

Смещение спектра сигнала

Пусть сигнал обладает спектральной плотностью причем максимальная частота в спектре сигнала ограничена частотой . Умножим сигнал на гармоническую функцию причем . Получим сигнал определим его спектральную плотность:

=

= =

=

Первый интеграл представляет собой спектральную плотность сигнала на частоте ( ), а второй – на частоте ( ). Таким образом, имеем

Отсюда видно, что при умножении сигнала на гармоническую функцию с частотой имеет место расщепление спектра на две части, смещенные на . Графическая интерпретация этого эффекта показана на рис.7 на примере четного прямоугольного импульса.

             

Рис. 7

Сигнал, полученный в результате перемножения импульса на называется радиоимпульсом.

Данное свойство используется при получении модулированных сигналов

Произведение двух сигналов

Пусть сигнал s(t)=f(t)g(t), причем функции – сомножители обладают спектральными плотностями и . Определим спектральную плотность произведения. По определению

Подставим в этот интеграл одну из функций, например g(t), выраженную через ее спектральную плотность, т.е.

тогда получим

Здесь, чтобы не путать переменные интегрирования во внутреннем интеграле, используется величина u для обозначения в нем текущей частоты.

Это выражение можно привести к виду, осуществив перестановку соответствующих членов:

Внутренний интеграл представляет собой спектральную плотность сигнала f(t) на частоте  -u, т.е. . Таким образом,

Такого типа интеграл называется сверткой ( с коэффициентом ) спектров сигналов – сомножителей. Итак, произведению сигналов во временной области соответствует свертка сигналов в частотной области ( свертка спектров с коэффициентом ).

Используем это свойство для определения интеграла от произведения двух временных функций. Для этого достаточно определить свертку спектров при  =0, т.е.

Заменяя u на  , F(-  на F^*(  , получаем

Если g(t)=f(t), то

Величина определяет спектральную плотность энергии сигнала. Правая и левая части определяют полную энергию сигнала.

Произведение спектров двух сигналов

Пусть имеется сигнал s(t), спектральная плотность которого представляет собой произведение вида , где спектру соответствует сигнал f(t), а спектру - сигнал g(t). Выразим сигнал s(t) через сигналы g(t) и f(t).По определению:

(*)

Проведя выкладки, аналогичные выкладкам предыдущего параграфа, получим:

(**)

т.е. произведению сигналов в частотной области (спектров) соответствует свертка сигналов во временной области. Это свойство преобразования Фурье используется при анализе прохождения сигналов через линейные цепи .

Дифференцирование и интегрирование сигналов

Обратное преобразование Фурье для сигнала s(t) представляет собой сумму гармонических составляющих конечной амплитуды ,если s(t) периодическая функция, или составляющих бесконечно малой амплитуды S(  )d  для непериодического сигнала:

 

(*)

или

(**)

Дифференцирование по времени сигнала эквивалентно дифференцированию по времени правых частей соотношения    (*) или (**):

Таким образом, периодическому сигналу соответствует спектр с амплитудами

.

а спектральной плотности сигнала

соответствует спектральная плотность

Аналогично можно показать, что если

то в случае периодического сигнала коэффициенты ряда Фурье

,

и в случае непериодического сигнала

Использовать данное свойство преобразования Фурье целесообразно только для сигналов, у которых или S(0)=0, т.е. для сигналов с нулевой площадью:

т.к. иначе получим что означает бесконечность энергии проинтегрированного сигнала, тчо невозможно.