Связь между огибающей спектра периодического сигнала и спектральной плотностью непериодического сигнала той же формы
Сравнивая выражения для
и
комплексной огибающей ряда Фурье
для
периодического сигнала, видим, что
отличие состоит лишь в коэффициенте
1/T. Следовательно, можно записать
связь
.
Таким образом, если периодический сигнал
образован из непериодического сигнала
s(t), то можно определить огибающую
амплитудного спектра через модуль
спектральной плотности. Огибающая ФЧС
и ФЧХ непериодического сигнала совпадают.
Пусть для сигнала s(t) найдена
спектральная плотность
(см.рис.2,
а). Тогда для построения АЧС и ФЧС
периодического сигнала той же формы
достаточно построить огибающие и
провести линии, соответствующие частотам
составляющих (рис.2,б).
а) б)
Рис. 2
Несмотря на сплошной характер спектральной плотности непериодического сигнала, для простоты её часто называют "спектром".
Распределение энергии в спектре непериодического сигнала
Величина
определяет полную энергию сигнала s(t).
Выразим энергию через спектральную плотность:
Следовательно,
Это соотношение носит название "равенство Парсеваля". Квадрат модуля спектральной плотности имеет смысл спектральной плотности энергии сигнала.
Примеры. Одиночный прямоугольный импульс. Экспоненциальный импульс. Гауссов импульс
Пусть дан прямоугольный импульс с амплитудой А и длительностью . На оси времени он задан положением середины импульса t0 (рис.3).
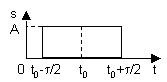
Рис. 3
Тогда аналитически сигнал можно описать следующим образом.
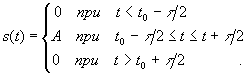
Определим выражение для спектральной плотности.
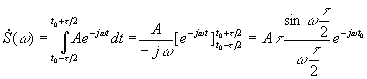
Если это выражение разделить на Т и подставить вместо частоту n 1 , то получим уже известное выражение для АЧС последовательности прямоугольных импульсов:
Нули модуля спектральной плотности расположены на частотах =2 k/ , где k= 1, 2,... На частоте =0 спектральная плотность равна S( 0 )=A .
На рис.4 изображены графики АЧХ и ФЧХ прямоугольного импульса с учетом знака синуса.
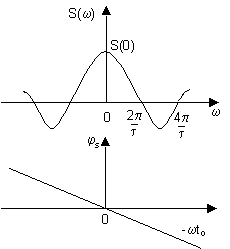
Рис. 4
Полная энергия импульса равна
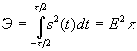
Энергия сигнала, ограниченного первым лепестком спектральной плотности, составляет 90% мощности прямоугольного импульса.
Определим спектральную плотность экспоненциального импульса вида
изображенного на рис.5.
а) б)
Рис. 5
В этом случае
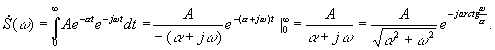
Графики АЧХ и ФЧХ показаны на рис.5,б. На
частоте
=0 S(0)=A/
; при
<<
;
при
>>
;
на частоте
=
.
Таким образом, спектральная плотность
экспоненциального импульса не имеет
нулей и плавно уменьшается с увеличением
частоты.
Колоколообразный (гауссовский) импульс определяется выражением
Во временной области он изображен на рис. 6а. Условно длительность такого импульса определяют по уровню е-1/ 2 от амплитуды.
Спектральная плотность определяется через интеграл Фурье:
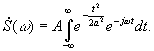
После замены переменных:
где
,
интеграл приводится к виду
причем
Окончательно получаем
где
Таким образом, спектральная плотность гауссовского импульса является действительной функцией частоты s=0) (т.к. сигнал задан четным образом), модуль которой также является гауссовским импульсом (рис. 6б).
а) б)
Рис. 6
Т.е. гауссовскому спектру соответствует гауссовский импульс, причем чем шире полоса спектра, определяемая на уровне е-1/ 2 от максимума величиной b, тем уже условная длительность импульса, определяемая величиной а=1/b, и наоборот.