
- •Предмет теория электрической связи
- •Информация, сообщение, сигнал
- •Обобщенная схема системы передачи информации
- •Модели канала связи
- •Описание сигналов
- •Энергетические характеристики сигналов
- •Гармоническое колебание
- •Обобщенный ряд Фурье
- •Тригонометрический ряд Фурье
- •Действительный частотный спектр сигнала
- •Комплексный ряд Фурье и спектр сигнала
- •Распределение мощности в спектре периодического сигнала
- •Огибающая спектра периодического сигнала
- •Пример: периодическая последовательность прямоугольных импульсов
- •Связь между огибающей спектра периодического сигнала и спектральной плотностью непериодического сигнала той же формы
- •Распределение энергии в спектре непериодического сигнала
- •Примеры. Одиночный прямоугольный импульс. Экспоненциальный импульс. Гауссов импульс
- •Линейная комбинация сигналов
- •Сдвиг сигнала во времени
- •Смещение спектра сигнала
- •Произведение двух сигналов
- •Взаимная заменяемость частоты и времени в паре преобразований Фурье
- •Преобразование Лапласа на плоскости комплексной частоты
- •Основные свойства преобразования Лапласа
- •Взаимная и автокорреляционные функции сигнала
- •Связь между автокорреляционной функцией и спектром сигнала
- •Акф периодического сигнала
- •Общие определения
- •Амплитудно-модулированные радиосигналы
- •Радиосигналы с угловой модуляцией
- •Амплитудно-частотная модуляция
- •Узкополосный сигнал
- •Классификация методов анализа прохождения сложных сигналов через линейные цепи
- •Частотная передаточная характеристика цепи
- •Переходная и импульсная характеристики цепи
- •Обоснование частотного метода
- •Чаcтотные фильтры. Классификация и основные параметры
- •Прохождение частотно-модулированных колебаний через колебательную систему
- •Колебательные цепи при импульсном воздействии
- •Сущность операторного метода
- •Примеры применения операторного метода
- •Виды случайных процессов
- •Широкополосный случайный процесс. Белый шум
- •Узкополосный случайный процесс
- •Задачи и этапы синтеза
- •Спектр дискретизированного сигнала
- •Статические и динамические параметры нелинейного элемента
- •Основные показатели и характеристики усилителя
- •Общие сведения о сигналах
- •Преобразователь частоты
Модели канала связи
Каналом связи называют совокупность устройств, имеющих один вход и один выход, и предназначенных для передачи сигналов на расстояние.
В зависимости от вида представления сообщений на входе и выходе канала связи различают непрерывные, дискретные и полунепрерывные каналы.
В непрерывных каналах связи сигналы на входе и выходе представляются в аналоговой или дискретно-аналоговой форме.
В дискретных каналах связи сообщения на входе и выходе представлены в цифровой форме. Такой канал обычно состоит из непрерывного канала, к которому на входе подключаются устройства формирования и кодирования цифровых сигналов, а на выходе - решающее (обрабатывающее) устройство, служащее для опознавания переданных сигналов. В теории информации дискретный канал рассматривается как некоторое устройство со статистическими связями между входом и выходом, отражающими действия помех.
В полунепрерывных каналах на одном из концов ( входе или выходе) сообщение может быть представлено в цифровой форме, а на другом - в аналоговой или дискретной
Описание сигналов
Любой электрический сигнал можно рассматривать как меняющуюся во времени электрическую величину ( ток или напряжение). Математическое выражение, по которому для любого момента времени t можно вычислить значение сигнала s(t), является детерминированной моделью этого сигнала. Наиболее часто такой выбор осуществляется на основе временнОй диаграммы электрического сигнала.
Для математического описания сигналов используют как вещественные, так комплексные функции.
Сигнал s(t) называется периодическим
с периодом T, если s(t)=s(t+kT),
где k - любое целое число. Периодические
сигналы, таким образом, определены на
всей оси времени, т.е.
![]() <t<
<t<![]() . Для периодического сигнала достаточно
задать математическое описание на
интервале времени, совпадающем с его
периодом. Величина F1=1/T
называется частотой повторения сигнала.
. Для периодического сигнала достаточно
задать математическое описание на
интервале времени, совпадающем с его
периодом. Величина F1=1/T
называется частотой повторения сигнала.
Сигналы, не являющиеся периодическими, называются непериодическими. Их необходимо описывать на всей оси времени от до . Если непериодический сигнал отличен от нуля на некотором определенном интервале времени, то такой сигнал называется ограниченным во времени.
По скорости изменения различают медленно меняющиеся сигналы - ток или напряжение, образованные в результате преобразования информации в электрический сигнал, и радиосигналы, скорость изменения которых много больш
Энергетические характеристики сигналов
Основными энергетическими характеристиками сигнала s(t) являются его мощность и энергия.
Мгновенная мощность p(t) для вещественного сигнала определяется как
![]()
а для комплексного как
![]()
где знак " * " означает комплексно сопряженную функцию.
Если s(t) - напряжение или ток, то p(t) есть мгновенная мощность, выделяемая на сопротивлении 1 Ом.
Энергия сигнала на интервале ( t2 , t1 ) определяется как интеграл от мгновенной мощности
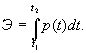
Отношение
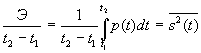
имеет смысл средней на интервале ( t2 , t1 ) мощности.
Для неограниченных по времени периодических сигналов определяют среднюю за период мощность
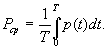
Гармоническое колебание
Одним из наиболее часто используемых типов детерминированных периодических сигналов является гармоническое колебание. Это обусловлено несколькими факторами. Во-первых, гармоническое колебание наиболее просто технически воспроизвести; во-вторых, только гармонический сигнал, проходя через линейные цепи, сохраняет свою форму; в-третьих, большинство используемых в радиоэлектронике сигналов с помощью аппарата Фурье может быть представлено суммой гармонических составляющих.
Гармоническое колебание аналитически можно записать как функцию косинуса или синуса. Чаще применяют функцию косинуса:
![]()
где Am - амплитуда, 0 - частота, 0 - начальная фаза. Величина ( 0 t0 )= (t) определяет полную фазу. Частота и период гармонического сигнала связаны соотношениями:
![]()
где 0 - циклическая частота, ее размерность радианы/сек, f 0 -частота, число колебаний за секунду, ее выражают в герцах (Гц, Hz); 103 Гц = 1 кГц (килогерц), 106 Гц = 1 МГц (мегагерц), 109 Гц=1 ГГц (гигагерц). Гармоническое колебание полностью характеризуется тремя параметрами: частотой (или периодом), амплитудой и фазой.
Функция s(t) определяет гармонический сигнал на временной плоскости (рис.1).
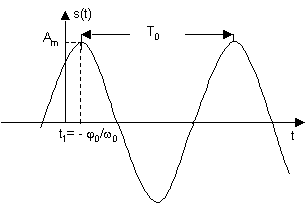
Рис. 1
Если в качестве оси абсцисс выбрать частоту, а оси ординат - амплитуду и фазу то можно получить представление гармонического сигнала на частотной плоскости, причем для удобства графики амплитуда - частота и фаза - частота рисуют отдельно (см. рис. 2).
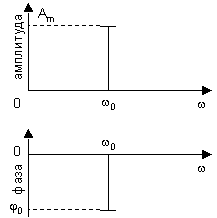
Рис. 2
В соответствии с формулами Эйлера действительный гармонический сигнал можно записать в виде
![]() .
.
Сигнал вида
![]() будем
называть комплексным. В соответствии
с теорией комплексных функций можно
записать
будем
называть комплексным. В соответствии
с теорией комплексных функций можно
записать
![]()
и для любого момента времени можно
построить на комплексной плоскости
вектор функции
![]() (рис.3),
который называют векторной диаграммой.
(рис.3),
который называют векторной диаграммой.
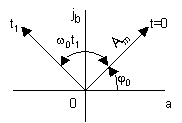
Рис. 3
Вектор вращается с угловой скоростью
. На рисунке показаны положения вектора
в моменты времени t=0 и t1![]() 0. При t=2
вектор попадает в положение t=0.
Поэтому обычно векторную диаграмму
представляют для t=0, а вращение
вектора обозначают скоростью вращения
(см. рис. 4 ), сам же вектор отображают
комплексным числом
0. При t=2
вектор попадает в положение t=0.
Поэтому обычно векторную диаграмму
представляют для t=0, а вращение
вектора обозначают скоростью вращения
(см. рис. 4 ), сам же вектор отображают
комплексным числом
![]() ,
называемым комплексной амплитудой
,
называемым комплексной амплитудой
![]() ,т.е.
,т.е.
![]()
где точка над амплитудой отражает комплексный характер этой величины.
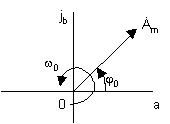
Рис. 4
Действительная часть функции есть проекция на действительную ось, т. е.
![]()
Если действительный гармонический сигнал представить в виде суммы комплексных по формуле Эйлера, то для построения его комплексно-сопряженной части на частотной плоскости придется использовать и область отрицательных частот. Это показано на рис.5.
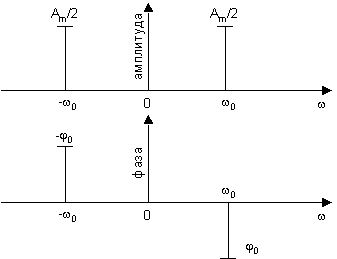
Рис. 5
Использование понятия комплексной амплитуды гармонического сигнала значительно упрощает расчет электрических цепей. Метод, основанный на использовании этого понятия, называется методом комплексных амплитуд.
Покажем, что линейные преобразования гармонического сигнала легко свести к тем же преобразованиям комплексных амплитуд.
Пусть имеем сумму гармонических колебаний с одинаковой частотой:
![]() .
.
Известно, что сумма гармонических функций одной частоты есть также гармоническая функция этой частоты, амплитуда которой равна
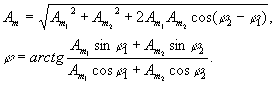
Пользуясь же понятиями комплексных амплитуд и векторным представлением имеем (рис.6):
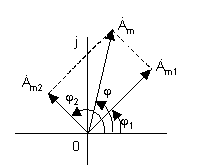
Рис. 6
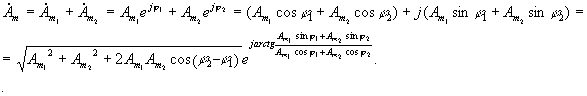
Таким образом, линейная комбинация нескольких гармонических сигналов с одной и той же частотой есть гармоническое колебание с той же частотой, комплексная амплитуда которого соответствует этой линейной комбинации.
Покажем, как меняется комплексная амплитуда при таких операциях как дифференцирование и интегрирование.
Пусть
![]() .
.
Тогда
![]() ;
;
откуда видим, что
![]() ,
т.е. дифференцирование гармонической
функции соответствует умножению ее
комплексной амплитуды на величину
,
т.е. дифференцирование гармонической
функции соответствует умножению ее
комплексной амплитуды на величину
![]() .
.
При интегрировании имеем
![]()
т.е. интегрирование гармонической
функции эквивалентно делению комплексной
амплитуды на частоту и повороту фазы
на
![]() ,
т.е.
,
т.е.
![]()
На векторных диаграммах операция дифференцирования соответствует повороту фазы на +900, а интегрирования - повороту на -900 относительно исходного вектора.
Задачи
Задача 2.1
Импульсный сигнал u(t), имеющий размерность напряжения, описывается формулой :
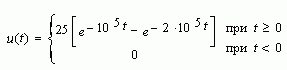
Постройте график импульса. Определите
максимальное значение сигнала Umax
и соответствующее ему tmax.
Вычислите длительность импульса ![]() , определив её как длину отрезка времени
от нуля до той точки, в которой мгновенное
значение сигнала уменьшается в 10 раз
по сравнению с Umax.
, определив её как длину отрезка времени
от нуля до той точки, в которой мгновенное
значение сигнала уменьшается в 10 раз
по сравнению с Umax.
Задача 2.2
Представить напряжение вида ![]() на временной и частотной плоскостях.
Построить векторную диаграмму . Записать
комплексную амплитуду.
на временной и частотной плоскостях.
Построить векторную диаграмму . Записать
комплексную амплитуду.
Задача 2.3
Гармонический ток задан комплексной
амплитудой:
![]() и
частотой f = 1МГц
Построить
его график на временной и частотной
плоскостях, а также векторную диаграмму.
и
частотой f = 1МГц
Построить
его график на временной и частотной
плоскостях, а также векторную диаграмму.
