Амплитудно-частотная модуляция
При одновременном изменении амплитуды и фазы (за счет изменения мгновенной частоты) получается АЧМ – колебание. В общем виде его можно представить как
Каждое слагаемое можно представить как
произведение низкочастотной функции
и гармонического сигнала с частотой
,
что свидетельствует о соответствующем
сдвиге спектра низкочастотных сигналов
в
область частоты
,
и дальнейшем векторном (квадратурном)
сложении.
Пусть спектральная плотность косинусной и синусной функции равны
Тогда
в соответствии с теоремой о переносе
спектра имеем
Если при АМ амплитуды боковых имеют симметричные фазы, а при ЧМ – фазы нечетных боковых отличаются на ,то спектр АЧМ сигнала может оказаться несимметричным (см. Рис.11).
Рис. 11
Пусть модулирующей функцией как для амплитуды, так и для частоты является низкочастотный гармонический сигнал с частотой ,причем
т.е. обе функции - четные относительно
.
Тогда
Для малых m получим
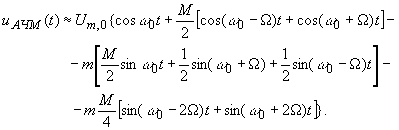
Для
,получается
следующий амплитудный спектр
результирующего колебания (Рис.12,а).
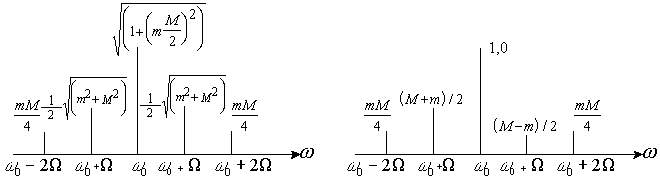
а) б)
Рис. 12
Если же
то
результирующий спектр получится
несимметричным (Рис.12,б). Асимметрия
спектра при АУМ может рассматриваться
как показатель паразитной УМ при АМ или
паразитной АМ при УМ.
Узкополосный сигнал
Сигнал называется узкополосным (УПС), если ширина его спектра значительно меньше средней частоты (рис.13):
Рис. 13
Типичными представителями УПС являются модулированные радиосигналы. К УПС можно также отнести несколько радиосигналов со своими несущими, занимающие вместе достаточно узкую полосу частот.
В первом приближении для анализа
прохождения УПС через радиоэлектронные
цепи такой сигнал можно представить
гармоническим на средней частоте. Более
лучшее приближение дает представление
УПС в виде квазигармонического колебания,
у которого медленно (по сравнению с
)
меняются мгновенные амплитуда и частота.
В этом случае полагается, что за достаточно
короткое время (меньшее, чем изменения
амплитуды и частоты), сигнал можно
считать гармоническим.
В общем случае УПС можно представить в виде
где
и
-медленно
меняющиеся функции времени.
Для классических АМ и ЧМ колебаний
средняя частота совпадает с несущей
частотой сигнала. Для однозначного и
наиболее оптимального выбора
применяется
аппарат преобразования Гильберта,
согласно которому для заданного УПС
находится
сопряженная функция
,определяемая
как
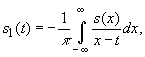
при этом
Огибающая, определённая таким образом,
совпадает с сигналом
в
моменты времени, где
,т.е.
имеют
общие касательные, причем в точках
касания функция
близка
к максимумам (Рис.14):
Рис. 14
Для сигнала вида
сопряженная
по Гильберту функция равна
а
для
.
Исходя из этих соотношений для
гармонического сигнала
огибающая
и частота равны соответственно:
как и следовало ожидать. Если же выбрать произвольным образом среднюю частоту, то даже для гармонического сигнала можно получить некую достаточно сложную огибающую, не соответствующую действительности.
Рассмотрим в качестве примера УПС, состоящий из суммы гармонических составляющих:
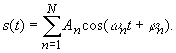
Для такого сигнала
откуда
После преобразований можно получить следующее выражение для мгновенной частоты
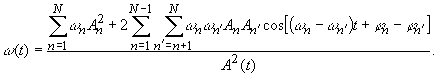
Для двухчастотного сигнала (N=2) имеем
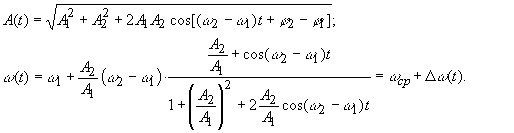
Таким образом, сумму двух близко
расположенных по частоте (
)
сигналов можно записать в виде
квазигармонического колебания:
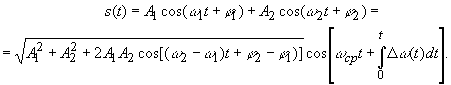
Рис.15 иллюстрирует примерный вид сигнала,
состоящего из двух гармонических
сигналов с равными амплитудами (
=
=
).
Рис. 15
Ниже на рис.
16 и рис.
17 приведены нормированные
графики одного периода огибающей и
мгновенной частоты: бигармонического
сигнала для
,
0,5 и 0,1.
Рис. 16
Из графиков рис.
15, 16
и 17
видно, что при взаимодействии двух
сигналов с равными амплитудами огибающая
амплитуд меняется от удвоенной амплитуды
каждого до нуля. Причем в нуле огибающей
фаза скачком меняется на
,что
формально означает переход через
бесконечность (разрыв) мгновенной
частоты, а в остальное время
При уменьшении амплитуды одного из сигналов мгновенная частота ( рис.17 ) непрерывно меняется и при малом k средняя частота близка к частоте большего сигнала.
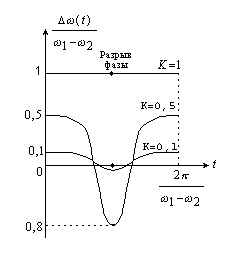
Рис. 17
При малом k огибающую можно представить в приближенном виде
откуда видно, что огибающая в этом случае линейно зависит от амплитуды малого сигнала при постоянной амплитуде большого. Если малый сигнал в свою очередь будет квазигармоническим
т.е.
то
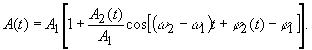
Таким образом результирующая огибающая содержит линейную информацию об изменении амплитуды и фазы малого сигнала, что дает возможность в приемнике выделить эту информацию без нелинейных искажений.