6.4. Резонанс

Резонанс – резкое возрастание амплитуды вынужденных колебаний осциллятора: А =max. Это возможно, когда ω ≈ ω₀.

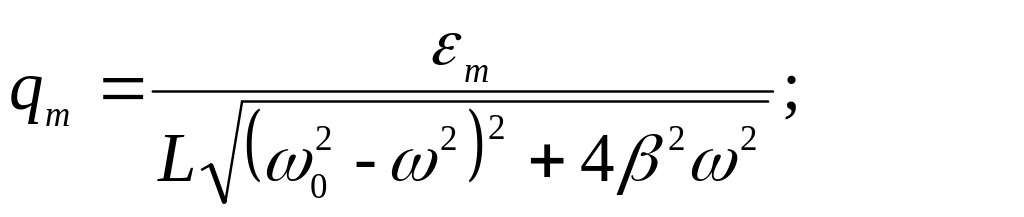
Знаменатель должен быть минимальным:

(ω₀² – ω²)² + 4 β² ω² = min,

т.е. производная должна быть равна 0. Взяв производную по ω, получаем: .

Если β = 0 (нет R), то ω_рез = ω₀ и q_m = ∞. Когда ω = 0, то q_m = ε_m.

На рисунках представлены резонансные кривые для q_m и I_m. Резонансные кривые для U_Cm такие же как и для q_m.

.

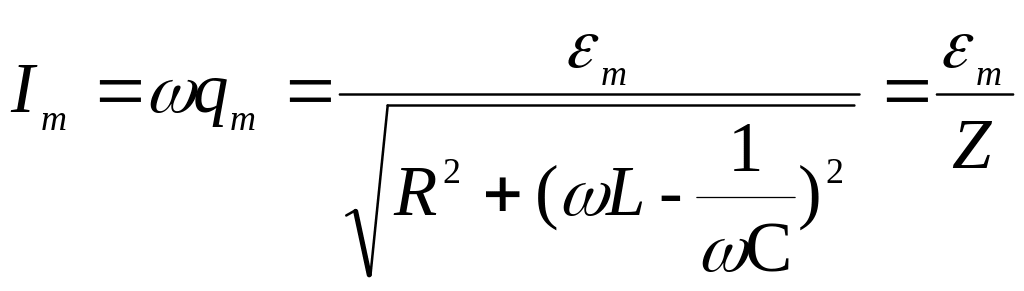К огда ω = 0, то I_m = 0;

I_m = max, если 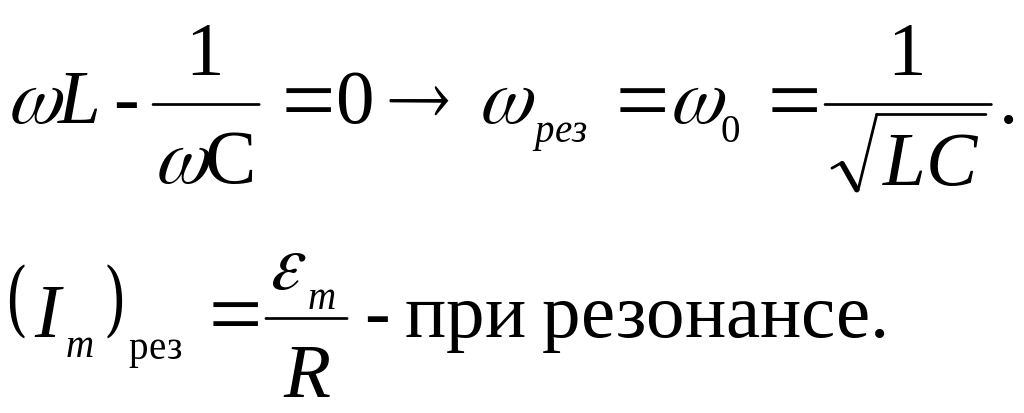Форма резонансных кривых связана с добротностью контура Q. Добротность контура связана с шириной резонансной кривой: Δω – ширина резонансной кривой. Δω находится на «высоте», равной 0,7 от максимальной, т.е. в резонансе.

Следовательно, острота резонансной кривой связана с добротностью контура.

Из векторной диаграммы: 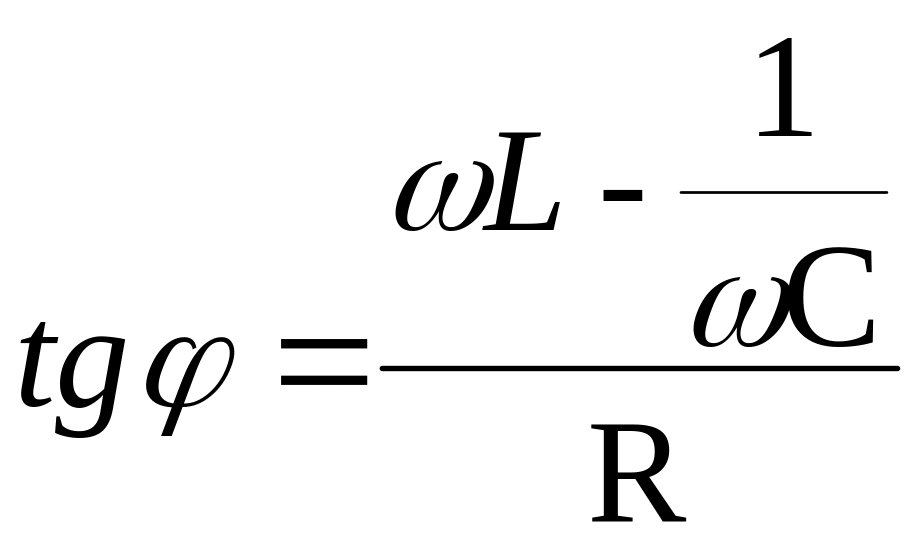, φ – сдвиг по фазе между током I и ε.

При резонансе I_m = max и т.е.сила тока I и приложенное напряжение ε изменяются синфазно. Тогда Z = min → Z = R →

U

I_m·R = U_R = ε_m

_R = ε = U, т.е. внешнему напряжению, и U_mC = U_mL, но противоположны по фазе.

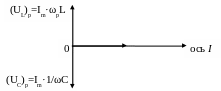
Такой резонанс (последовательный резонанс) называется резонансом напряжений.

.

Т.к. Q > 1, то U_L > U и U_С > U, поэтому резонанс напряжений используется в технике для усиления колебаний напряжения какой-либо определенной частоты.

Резонанс напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, т.к. иначе может наблюдаться пробой.

Лабораторная работа № 18. Исследование затухающих колебаний в колебательном контуре

Цель работы: изучение затухающих колебаний.

Приборы и принадлежности: осциллограф, колебательный контур, звуковой генератор ГЗ – 111.

Методика и техника эксперимента

К олебательным контуром называется цепь, состоящая из конденсатора С, катушки индуктивности L и омического сопротивления R. Если зарядить конденсатор до разности потенциалов U, а затем дать ему возможность разряжаться через индуктивность L, то в колебательном контуре возникают свободные колебания тока, заряда на обкладках конденсатора и напряжения между обкладками конденсатора. В процессе колебаний, энергия электрического поля заряженного конденсатора преобразуется в энергию магнитного поля катушки индуктивности и, наоборот, энергия магнитного поля преобразуется в электрическую энергию. При протекании тока в контуре в активном сопротивлении выделяется джоулево тепло, что приводит к потере энергии и затуханию колебаний. В связи с этим, с течением времени амплитуда колебаний уменьшается так, как показано на рисунке.

Выведем уравнение затухающих колебаний. Полагая, что мгновенные значения токов и напряжений удовлетворяют законам, установленным для цепей постоянного тока, применим к колебательному контуру второе правило Кирхгофа:

I·R + U_С = ε_S, (6.5)

где IR – падение напряжения на резисторе; U_С = – напряжение на конденсаторе; ε_S = – L – ЭДС самоиндукции.

Так как I = , а q = C·U, тогда I = C . Найдем производную силы тока: . Подставляя эти выражения в уравнение (6.5), получим:

+ + = 0. (6.6)

Разделив уравнение (6.6) на LC получим:

+ + = 0. (6.7)

Выражение (6.7) представляет собой дифференциальное уравнение затухающих колебаний, возникающих в колебательном контуре.

Решением этого уравнения является функция:

U = U₀ cos(ωt+φ), (6.8)

где β = R/2L – коэффициент затухания.

Так как циклическая частота собственных колебаний контура равна ω₀² = 1/LC, то уравнение (6.7) можно представить в виде:

+ 2β + ω₀²U = 0. (6.9)

U₀ = U_m – амплитуда затухающих колебаний;

ω = – частота затухающих колебаний; φ – начальная фаза.

Из выражения для частоты ω следует, что затухающие колебания в контуре возникают лишь в том случае, если: ω₀² >β²; > ; R < 2 .

Если R > , то колебания в контуре не возникают, а происходит, так называемый апериодический разряд конденсатора.

Для характеристики степени затухания колебаний, кроме коэффициента затухания β, используют также логарифмический декремент затухания.

Логарифмическим декрементом затухания λ называется натуральный логарифм отношения двух амплитуд напряжения U_m, разделенных интервалом времени, равным периоду колебаний Т:

λ = ln , (6.10),

где U_m1 = U₀ ; U_m2 = U₀ .

Подставив значения U_m в формулу (6.8), получим:

λ = β·T. (6.11)

Принципиальная схема для получения затухающих колебаний представлена ниже:

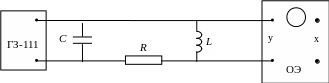
Она представляет собой колебательный контур, состоящий из конденсатора С, катушки индуктивности L и сопротивления R. Колебания в контуре наблюдаются с помощью осциллографа ОЭ. Для возбуждения колебаний служит звуковой генератор ГЗ-111.

Порядок выполнения работы.

1. Включить установку.

2. На магазине сопротивлений установить сопротивление R_m = 0.

3. По шкале на экране осциллографа измерить величину первой и второй амплитуды напряжения U_m1 и U_m2 (цена деления шкалы 2 мм).

4. При помощи магазина сопротивлений задавать значения сопротивления

R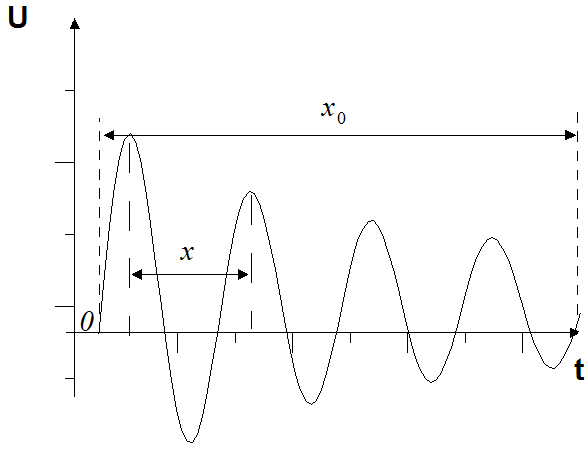 _m = 100, 200, 300 Ом.

5. Измерить амплитуды напряжения U_m1 и U_m2 для всех значений сопротивления R_m.

6. На экране осциллографа измерить величины:

x – расстояние между соседними максимумами

x_о – протяженность всей развертки.

7. Результаты измерений записать в таблицу 6.1.

Т а б л и ц а 6.1

Rm, Ом	Um1, В	Um2, В		х, м	х0, м	T, c	β, с-1	Rк, Ом	R, Ом	L, Гн	С, Ф
10
100
200
300

8. Вычислить значения логарифмического декремента затухания при всех значениях сопротивления магазина R_m по формуле 6.10.

9. Найти период колебаний Т по формуле:

T = , где ν = 400 Гц.

10. Определить коэффициент затухания β, используя формулу 6.11.

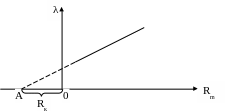
11. Построить график зависимости логарифмического декремента затухания λ от сопротивления магазина R_m. Продолжить график до пересечения с осью сопротивлений R_m и определить сопротивление катушки R_к, которое будет равно отрезку ОА.

12. Найти полное сопротивление контура R:

R = R_m + R_к.

13. Рассчитать значения индуктивности контура L при всех значения сопротивления R:

L = .

14. Найти среднее значение индуктивности контура Lср.

15. Используя формулу Томсона Т = 2π , определить емкость контура:

С = .