
- •При вращательном движении твердого тела под действием силы f работа равняется произведению момента этой силы на угол поворота.
- •6.Потенциальная энергия гравитационного взаимодействия
- •Потенциальная энергия упруго деформированного тела
- •7.Закон сохранения механической энергии системы. Из уравнения (10.15) следует,
- •Полная механическая энергия замкнутой консервативной системы не изменяется при любых перемещениях тел. Это утверждение называется законом сохранения механической энергии системы.
1.Работа при вращательном движении твердого тела. Согласно определению работы имеем:
A = F·ds = F·ds.
Поскольку ds = r·d, то получим следующее выражение для работы:
A = F·r·d = M·d.
При вращательном движении твердого тела под действием силы f работа равняется произведению момента этой силы на угол поворота.
Работа переменной силы при повороте тела на конечный угол равняется определенному интегралу от момента сил:
 .
.
Покажем, работа, совершаемая под действием равнодействующего момента сил, равна изменению кинетической энергии тела. Действительно,
A = M·d= I··d = I·(dw/dt)·w·dt = I·d(w2/2), где M - суммарный момент всех сил, действующих на тело.
Произведя интегрирование по углу, получим:
A12 = I·w22/2 - I·w12/2 = Eк.
2.Изменение кинетической энергии тела под действием силы Скалярная величина, равная половине произведения массы тела на квадрат его скорости называется кинетической энергией тела: Ek=(m*v^2)/2/ Кинетическая энергия тела (от гр. kinetikos — приводящий в движение) — это энергия, которой тело обладает вследствие движения. Кинетическую энергию тела относительно ИСО найдем, исходя из определения:
Eк = mi·vi2/2 = mi·(vi·vi)/2 = = mi·(Vc + vi')2/2 = = mi·Vc2/2 + mi·vi'2/2+ mi·Vc·vi'.
Полученное выражение представляет собой сумму трех слагаемых:
|
кинетической энергии переносного движения, обусловленного движением центра масс M·Vc2/2; |
|
кинетической энергии относительного движения, обусловленного движением частей тела в СО, связанной с центром масс, равной mi·vi'2/2 = Ic·w2/2; |
|
произведения полного импульса тела p' в СО, связанной с центром масс на скорость движения центра масс: Vc·mi·vi' = Vc·p'. Легко показать, что значение p' равняется нулю. p' = mi·vi' = mi·(vi - Vc) = mi·vi - mi·Vc = = mi·vi - M·Vc = 0, т.к. из определения центра масс и мгновенной скорости следует, что Vc = mi·vi/M. |
Кинетическая энергия твердого тела состоит из кинетической энергии его поступательного движения и энергии его движения E' относительно СО, связанной с центром масс. Это утверждение называется теоремой Кёнига. Eк = E' + M·Vc2/2.
Теорема Кёнига справедлива для любого плоского движения при котором центр масс перемещается в некоторой фиксированной плоскости, а вектор угловой скорости все время перпендикулярен к этой плоскости. Примером плоского движения является качение.
3.Потенциальная энергия
![]() —
скалярная
физическая
величина, характеризующая
способность некоего тела (или материальной
точки) совершать работу
за счет его нахождения в поле действия
сил. Другое определение: потенциальная
энергия — это функция координат,
являющаяся слагаемым в лагранжиане
системы, и описывающая взаимодействие
элементов системы[1].
Термин «потенциальная энергия» был
введен в XIX веке шотландским
инженером и физиком Уильямом
Ренкином.
—
скалярная
физическая
величина, характеризующая
способность некоего тела (или материальной
точки) совершать работу
за счет его нахождения в поле действия
сил. Другое определение: потенциальная
энергия — это функция координат,
являющаяся слагаемым в лагранжиане
системы, и описывающая взаимодействие
элементов системы[1].
Термин «потенциальная энергия» был
введен в XIX веке шотландским
инженером и физиком Уильямом
Ренкином.
Единицей измерения энергии в СИ является Джоуль.
Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.
Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.
Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.
Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
Ep = mgh,
где Ep — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
4.Свойства потенциальной
энергии.
1. Потенциальная энергия
является конечной, однозначной,
непрерывной функ¬цией механического
состояния системы.
2. Численное
значение потенциальной энергии зависит
от выбора уровня с нулевой потенциальной
энергией.
Как потенциальная энергия
может быть найдена по известной
консервативной силе, так и консервативная
сила может быть найдена по потенциальной
энергии:
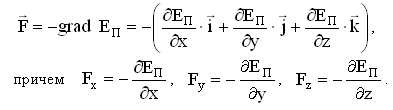
5. Связь силы и потенциальной энергии.
Каждой точке потенциального поля
соответствует, с одной стороны, некоторое
значение вектора силы
![]() ,
действующей на тело, и, с другой стороны,
некоторое значение потенциальной
энергии
,
действующей на тело, и, с другой стороны,
некоторое значение потенциальной
энергии
![]() .
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
.
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
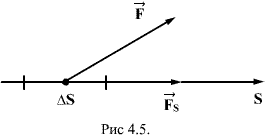
Для установления этой связи вычислим
элементарную работу
![]() ,
совершаемую силами поля при малом
перемещении
,
совершаемую силами поля при малом
перемещении
![]() тела,
происходящем вдоль произвольно выбранного
направления в пространстве, которое
обозначим буквой
тела,
происходящем вдоль произвольно выбранного
направления в пространстве, которое
обозначим буквой
![]() .
Эта работа равна
.
Эта работа равна
![]()
где
![]() -
проекция силы
на
направление
.
-
проекция силы
на
направление
.
Поскольку в данном случае работа
совершается за счет запаса потенциальной
энергии
,
она равна убыли потенциальной энергии
![]() на
отрезке оси
:
на
отрезке оси
:
![]()
Из двух последних выражений получаем
![]()
Откуда
![]()
Последнее выражение дает среднее значение на отрезке . Чтобы
получить значение в точке нужно произвести предельный переход:
![]()
Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :
![]()
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
![]()
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

в математике вектор
 ,
,
где а - скалярная функция х, у, z, называется
градиентом этого скаляра обозначается
символом
![]() .
Следовательно сила равна градиенту
потенциальной энергии, взятого с обратным
знаком
.
Следовательно сила равна градиенту
потенциальной энергии, взятого с обратным
знаком
|
