
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет - ФТИ
Кафедра – квантовой физики и нанотехнологий
Качественный рентгенофазовый анализ
Отчет по лабораторной работе № 1
по дисциплине Физика рентгеновских лучей
Выполнила студентка гр. НТ-08 __________ Рабинович К. С.
Принял __________ Финкельштейн А. Л.
Иркутск –2012
Теоретическая часть:
Рентгенофлуоресцентный анализ (РФА) — один из современных спектроскопических методов исследования вещества с целью получения его элементного состава, то есть его элементного анализа. С помощью него могут анализироваться различные элементы от бериллия (Be) до урана (U). Метод РФА основан на сборе и последующем анализе спектра, полученного путём воздействия на исследуемый материал рентгеновским излучением. При облучении атом переходит в возбуждённое состояние, сопровождающееся переходом электронов на более высокие квантовые уровни. В возбуждённом состоянии атом пребывает крайне малое время, порядка одной микросекунды, после чего возвращается в спокойное положение (основное состояние). При этом электроны с внешних оболочек либо заполняют образовавшиеся вакантные места, а излишек энергии испускается в виде фотона, либо энергия передается другому электрону из внешних оболочек (оже-электрон). При этом каждый атом испускает фотоэлектрон с энергией строго определённого значения, например железо при облучении рентгеновскими лучами испускает фотоны Кα = 6,4 кэВ. Далее соответственно по энергии и количеству квантов судят о строении вещества.
Способы рентгенофлуоресцентного анализа
Переход от измеренной интенсивности аналитической линии к содержанию определяемого элемента, как и в других спектральных методах, осуществляется с помощью образцов сравнения, состав которых известен. Для решения этой задачи разработан ряд приемов.
Способ разбавления пробы нейтральной средой. Чтобы сблизить химический состав анализируемых проб между собой, применяют их разбавление некоторой нейтральной средой; аналогично поступают и с образцами сравнения. После этого пробы анализируют прямым способом внешнего стандарта. Добавка нейтральной среды снижает интенсивность аналитической линии, поэтому такой прием годится, главным образом, для анализа проб с высоким содержанием определяемого элемента. С другой стороны, в качестве добавки целесообразно использовать слабопоглощающие материалы. Если же снижение чувствительности не оказывает особого влияния на результат анализа, в качестве добавки выгодно использовать «тяжелые» среды, т. е. материалы, обладающие значительной поглощающей способностью. Применение таких сред более эффективно сближает поглощательную способность анализируемых материалов, что позволяет использовать меньшие степени разбавления.
Способ разбавления получил широкое применение при анализе порошкообразных веществ путем их предварительного сплавления с флюсом. В этом случае не только устраняется влияние химического состава на интенсивность аналитических линий, но и обеспечивается получение однородного материала пробы.
Способ добавок. Если концентрация определяемого элемента в пробах мала, а сами пробы разнообразны по химическому составу, применяют способ добавок. В этом случае анализируемую пробу делят на две части, оставляя одну из них без изменения, а во вторую вводят известное количество определяемого элемента. Искомую концентрацию рассчитывают из соотношения
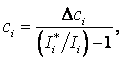 (14.155)
(14.155)
где
∆сi — величина
введенной добавки; ![]() и
и ![]() —
интенсивности аналитической линии в
пробах с добавкой и без нее.
—
интенсивности аналитической линии в
пробах с добавкой и без нее.
Способ добавок подробно рассматривался в предыдущих разделах справочника.
Способ внутреннего стандарта. Рассмотренные выше приемы анализа являются, в сущности, вариантами одного и того же способа — внешнего стандарта. Известны и другие его варианты, например, с введением поправок на поглощение (учет второго сомножителя в выражении 14.153). Другая группа приемов может по аналогии рассматриваться как способ внутреннего стандарта.
При работе по способу внутреннего стандарта в анализируемую пробу вводят известное количество элемента, не содержащегося в ней. Этот элемент называется внутренним стандартом или элементом сравнения. После измерения интенсивностей линий определяемого элемента IA и элемента сравнения IB концентрацию сA находят из соотношения
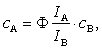 (14.156)
(14.156)
где сВ — концентрация элемента сравнения в пробе; Ф — коэффициент, величину которого определяют экспериментально с помощью образцов с известным содержанием элементов А и В:
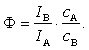 (14.157)
(14.157)
На практике обычно строят график зависимости IA / IB = f (сA) с помощью образцов известного состава и по нему находят искомую концентрацию.
При выборе элемента сравнения и экспериментальных условий анализа следует стремиться к тому, чтобы величина коэффициента Ф не зависела или слабо зависела от химического состава наполнителя анализируемых материалов. Основные рекомендации по выбору элемента сравнения сводятся к следующему.
1. Элемент сравнения должен находиться в форме, позволяющей произвести его точное дозирование в пробу (естественно, изначально он должен отсутствовать в анализируемых материалах).
2. Длина волны края поглощения для элемента сравнения должна быть по возможности ближе к длине волны края поглощения определяемого элемента. Кроме того, следует стремиться к тому, чтобы между краями поглощения сравниваемых элементов не находились линии третьего элемента М, так как в противном случае линии элемента М будут дополнительно возбуждать флуоресценцию элемента А или В в зависимости от того, чей край поглощения окажется наиболее длинноволновым.
3. Важно также, чтобы между сравниваемыми линиями элементов А и В отсутствовал край поглощения третьего элемента М, иначе одна из аналитических линий будет ослаблена вследствие эффекта избирательного поглощения.
4. При анализе разнообразных по химическому составу материалов за внутренний стандарт лучше брать элемент, край поглощения которого расположен с коротковолной стороны от края определяемого элемента.
5. При анализе материалов с небольшим содержанием искомого компонента за внутренний стандарт можно брать элемент, длина волны края поглощения которого больше длины волны края определяемого элемента.
Способ стандарта-фона. В качестве внутреннего стандарта можно использовать интенсивность рассеянного пробой первичного излучения Iр:
![]() (14.158)
(14.158)
где Dр — постоянная величина для выбранного участка спектра; t р — коэффициент рассеяния образцом излучения рентгеновской трубки; m р — массовый коэффициент поглощения рассеянного излучения образцом.
Отношение интенсивности аналитической линии к интенсивности рассеянного излучения можно представить в виде
![]() (14.159)
(14.159)
где
![]() (14.160)
(14.160)
Если выбрать для измерений рассеянного излучения участок спектра таким образом, что при изменении химического состава анализируемых проб будет выполняться условие
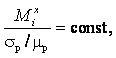 (14.161)
(14.161)
то выражение (14.159) может приближенно учитывать и матричные эффекты. На практике соотношение (14.159) заменяют линейной зависимостью
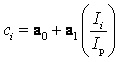 .
(14.162)
.
(14.162)
Постоянные а0 и а1 определяют с помощью образцов известного состава.
Подбор участка спектра, удовлетворяющего условию (14.161), представляет собой трудную задачу. Прежде всего, этот участок должен располагаться далеко от аналитической линии. Часто наилучшие результаты дает использование некогерентно рассеянного характеристического излучения рентгеновской трубки.
Выполнение условия (14.161) сильно зависит от особенностей используемой аппаратуры. Необходимо, чтобы рассеянное пробой излучение трубки было главным компонентом зарегистрированного фона. Это условие легче выполняется на приборах с фокусирующей рентгенооптикой (схемы Иогансона, Иоганна, Кошуа и т. д.).
Способ стандарта-фона находит широкое применение в практике анализа благодаря своей скорости и простоте, в связи с чем постоянно совершенствуется. Несколько видоизмененив способ, можно применять его и для определений высоких концентраций определяемого элемента. При этом учитывается, что интенсивность рассеянного пробой излучения регистрируется совместно с диффузным рассеянием аналитической линии кристаллом-анализатором. Величина вводимой поправки для учета этого эффекта пропорциональна интенсивности аналитической линии. Возможны варианты способа, учитывающие влияние некоторых мешающих элементов.
Многокомпонентный анализ. Число рентгеновских фотонов, излучаемых атомами в единицу времени, пропорционально количеству атомов, но в результате поглощения, рассеяния, дополнительного возбуждения и других видов взаимодействия рентгеновского излучения с веществом, а также вследствие влияния аппаратурных условий анализа регистрируемый аналитический сигнал i-го элемента от анализируемой пробы зависит от многих, подчас трудно учитываемых факторов, однако в общем случае может быть представлен как
![]() ,
(14.163)
,
(14.163)
где ![]() —
вектор концентраций всех элементов,
составляющих анализируемую пробу;
—
вектор концентраций всех элементов,
составляющих анализируемую пробу; ![]() —
вектор фундаментальных характеристик
отдельных элементов (атомных номеров,
длин волн излучения, коэффициентов
поглощения и рассеяния, выходов
флуоресценции и т. д.);
—
вектор фундаментальных характеристик
отдельных элементов (атомных номеров,
длин волн излучения, коэффициентов
поглощения и рассеяния, выходов
флуоресценции и т. д.); ![]() —
вектор, определяющий аппаратурные
условия возбуждения и регистрации
аналитических сигналов.
—
вектор, определяющий аппаратурные
условия возбуждения и регистрации
аналитических сигналов.
Автоматизированный многокомпонентный рентгенофлуоресцентный анализ основывается на использовании систем уравнений связи между интенсивностями аналитических линий и содержаниями элементов в пробе. К настоящему времени предложено несколько десятков уравнений связи, которые позволяют эффективно решать широкий круг аналитических задач.
Уравнения связи в РФА можно условно разделить на два типа в зависимости от того, физическая или математическая модель формирования аналитического сигнала положена в основу предлагаемого уравнения. Все уравнения связи, базирующиеся на физической модели возбуждения, можно вывести из формулы интенсивности рентгеновской флуоресценции (14.142) путем тех или иных преобразований и упрощений.
Далее, в уравнениях связи можно выделить три класса в зависимости от способа определения параметров и коэффициентов, характеризующих взаимные влияния элементов в анализируемом образце. Параметры и коэффициенты влияния могут быть вычислены теоретически, найдены экспериментально или полуэмпирическим путем, т. е. рассчитаны, а затем уточнены экспериментально с помощью образцов известного химического состава.
В уравнениях связи, основанных на математических моделях, численные значения коэффициентов влияния обычно устанавливаются экспериментально.
Каждый из выделенных таким образом типов и классов уравнений связи можно затем разделить на семейства, виды и разновидности, отличающиеся друг от друга более или менее существенными деталями их практической реализации.
Физические
модели и уравнения связи. Существует
два семейства уравнений связи, основанных
на физической модели возбуждения. В
первом используется выражение для F![]() в
явной форме, содержащее такие
фундаментальные параметры, как массовые
коэффициенты поглощения, скачки
поглощения, выходы флуоресценции и т.
д. Этот метод коррекции результатов
анализа получил название метода
фундаментальных параметров.
в
явной форме, содержащее такие
фундаментальные параметры, как массовые
коэффициенты поглощения, скачки
поглощения, выходы флуоресценции и т.
д. Этот метод коррекции результатов
анализа получил название метода
фундаментальных параметров.
Другое семейство уравнений связи базируется на преобразовании выражения для интенсивности разложением в ряд Тейлора или других преобразованиях к простому виду, не содержащему массовых коэффициентов поглощения и других фундаментальных параметров в явном виде. Такие методы в отечественной литературе получили название методов теоретических поправок, а в зарубежной литературе — методов коэффициентов влияния или методов α-коррекции.
Варианты метода фундаментальных параметров (МФП). Идея использования формулы для интенсивности аналитической линии при учете матричных эффектов в рентгеноспектральном микроанализе принадлежит Р. Кастену. В методе РФА впервые такой подход применили Дж. Крисс и Л. Биркс (1968 г.). В отечественной аналитической практике последователями этого направления были М.А. Блохин, Н.Ф. Лосев, В.П. Афонин и ряд других исследователей.
Выражение для искомой концентрации сx можно представить в виде
![]() (14.164)
(14.164)
Это выражение является исходным для всех вариантов МФП. Разновидности метода отличаются расчетными формулами для Fi. В частности, для этого можно использовать формулы (14.142–14.147).
Уравнения типа (14.164) универсальны и применимы в широком диапазоне концентраций и атомных чисел определяемых элементов в гомогенных образцах разнообразного химического состава. Метод успешно опробован при анализе сплавов на основе железа и никеля, сталей, сварочных шлаков и флюсов, покрытий сварочных электродов, осадочных пород, лунных образцов, сплавов на основе меди и железа, разнообразных типов горных пород на содержание основных породообразующих элементов и т. д. В принципе он не имеет ограничений на область применения в отношении состава анализируемых объектов.
Тем не менее, неопределенность в значениях коэффициентов поглощения, выходов флуоресценции и спектральном распределении первичного излучения, применимость только к гомогенным образцам, приближенность физической модели не позволяют полностью реализовать потенциальные возможности МФП. Однако при анализе образцов с широко меняющимися содержаниями компонентов он является наиболее гибким, не требует большого числа стандартных образцов состава и во всех случаях допускает автоматизацию трудоемких аналитических процедур.
Методы α-коррекции. В
методах фундаментальных параметров
и m -коррекции
выражения для ![]() ,
учитывающие матричные эффекты, получены
в пригодном для практики виде за счет
упрощения физической модели возбуждения
рентгеновской флуоресценции. В методах
α-коррекции это достигается путем
разложения величины
,
учитывающие матричные эффекты, получены
в пригодном для практики виде за счет
упрощения физической модели возбуждения
рентгеновской флуоресценции. В методах
α-коррекции это достигается путем
разложения величины ![]() в
ряд Тейлора в некоторой точке пространства
концентраций в окрестности стандартного
образца:
в
ряд Тейлора в некоторой точке пространства
концентраций в окрестности стандартного
образца:
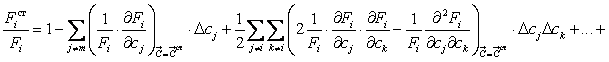 (14.165)
(14.165)
Здесь ![]()
![]() .
(14.166)
.
(14.166)
В качестве влияющих рассматриваются все элементы, кроме одного, произвольно выбранного элемента m. Удобно выбирать m = i. Обозначая коэффициент влияния j-го элемента на интенсивность аналитической линии i -го элемента как
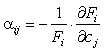 (14.167)
(14.167)
и ограничиваясь первым членом разложения (14.165), получим:
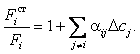 (14.168)
(14.168)
Подставляя (14.168) в (14.164), получим базовое уравнение для разновидностей методов α-коррекции
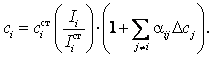 (14.169)
(14.169)
