
Молек. Термодин._практикум
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
МОЛЕКУЛЯРНАЯ ФИЗИКА ТЕРМОДИНАМИКА
ПРАКТИКУМ ПО ФИЗИКЕ
Издательство Иркутского государственного технического университета
2008
УДК 53(075.8) ББК 22.3
Рецензенты: д-р физ.-мат.- наук, профессор, зав. кафедрой физики ИГУ Л.А. Щербаченко;
д-р физ.-мат. наук, профессор, зав. кафедрой ТОЭ ИрГУПС Саламатов В.Н.
Редактор |
Л.К. Черкашина |
Компьютерный набор |
Т.В. Шинкова, Е.Л. Липовченко |
Авторы: Липовченко Е.Л., Рябцева Г.Г., Шинкова Т.В., Каницкая Л.В., Первушкина Э.И., Николаева М.З.
Молекулярная физика. Термодинамика: практикум по физике / Е.Л. Липовченко и др. . - Иркутск: Изд-во ИрГТУ, 2008. – 73с.
Содержит сведения об основных понятиях, определениях, законах молекулярной физики и термодинамики, описание методики и техники выполнения экспериментальных заданий.
Предназначен для студентов инженерных специальностей технических вузов направлений 550000 «Технические науки», 540000 «Профессиональное обучение».
Рекомендован к изданию ученым советом ИрГТУ
© Иркутский государственный технический университет, 2008
2
ОГЛАВЛЕНИЕ |
|
Введение………………………………………………………………………...….... |
5 |
1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ.. |
6 |
Исходные понятия и определения молекулярной физики |
|
и термодинамики.…………………………………………………….……….. |
6 |
Молекулярно-кинетическая теория идеальных газов…………………… |
9 |
Законы идеального газа………………………………………………..……… |
9 |
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)……………………………………………………. 10
Основное уравнение молекулярно-кинетической теории идеальных |
|
|
газов…………………………………………………………………………….. |
11 |
|
Молекулярно-кинетический смысл температуры……………………...…… |
13 |
|
Теория равновесных свойств идеального газа…………………………........ |
14 |
|
Положение о равнораспределении энергии |
|
|
по степеням свободы………………………………………………………….. |
14 |
|
Внутренняя энергия идеального газа………………………………………… |
15 |
|
Распределения Максвелла и Больцмана…………………………………….. |
15 |
|
Лабораторная работа 7 ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ БОЛЬЦМАНА |
18 |
|
Лабораторная работа |
ОПРЕДЕЛЕНИЕ УНИВЕРСАЛЬНОЙ ГАЗОВОЙ |
|
ПОСТОЯННОЙ…………………………………………………………………..................... |
22 |
|
2. ЯВЛЕНИЯ ПЕРЕНОСА В ТЕРМОДИНАМИЧЕСКИ НЕРАВНОВЕС- |
|
|
НЫХ СИСТЕМАХ………………………………………………………………. |
24 |
|
Виды процессов переноса…………………………………………………..... |
24 |
|
Число столкновений и средняя длина свободного пробега молекул………. |
25 |
|
Законы физической кинетики……………………………………………........ |
25 |
|
Лабораторная работа 13-1 ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОГО КОЭФФИ- |
|
|
ЦИЕНТА ВЯЗКОСТИ МЕТОДОМ ПУАЗЕЙЛЯ…………….............................................. |
28 |
|
Лабораторная работа 13-2 ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОГО КОЭФФИ- |
|
|
ЦИЕНТА ВЯЗКОСТИ МЕТОДОМ СТОКСА……………………………………………… |
32 |
|
Лабораторная работа ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОД- |
|
|
НОГО ПРОБЕГА И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА………….. |
34 |
|
Лабораторная работа |
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛО- |
|
ПРОВОДНОСТИ ТВЕРДЫХ ТЕЛ.......……………………………………………………… |
38 |
|
3

3. ТЕРМОДИНАМИКА………………………………………….…………..…… |
41 |
|||
Взаимосвязь между внутренней энергией, работой и теплотой |
|
|||
(п е р в ы й з а к о н т е р м о д и н а м и к и )……………………….……..……. |
41 |
|||
Применение первого начала термодинамики к изопроцессам…………… |
43 |
|||
Теплоемкость вещества…………………………………………..…………… |
45 |
|||
Уравнение Пуассона. Политропный процесс………………..…………….... |
47 |
|||
Работа газа при изопроцессах……………………………………….……….. |
48 |
|||
Обратимые и необратимые процессы. Циклы……………………………..... |
50 |
|||
Второе начало термодинамики………………………………………….…..... |
52 |
|||
Третье начало термодинамики…………………………………….…………. |
56 |
|||
Реальные газы. Уравнение Ван-дер-Ваальса………... …………….………... |
56 |
|||
Лабораторная работа 9 |
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКО- |
|
||
СТЕЙ ГАЗОВ |
СP |
МЕТОДОМ КЛЕМАНА ДЕЗОРМА……………………………... |
57 |
|
|
||||
|
CV |
|
||
|
|
|
||
Лабораторная работа 11 |
ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ ПРИ |
|
||
ИЗОХОРИЧЕСКОМ ПРОЦЕССЕ В ГАЗЕ……………………............................................. |
60 |
|||
Лабораторная работа 10 |
ОПРЕДЕЛЕНИЕ АДИАБАТИЧЕСКОЙ ПОСТО- |
|
||
ЯННОЙ СP ПО СКОРОСТИ ЗВУКА В ВОЗДУХЕ …………..................................
CV
4. СВОЙСТВА ЖИДКОСТЕЙ………………………………….……...................
Поверхностное натяжение…………………………….…………………......
Лабораторная работа 12 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ………………………………………………….
Заключение……………………………………………………………………………
Библиографический список……………………………………………….………..
Приложение…..………………………………………………………………….......
63
66
66
68
71
72
73
4
ВВЕДЕНИЕ
Úsus mаgίster est optimus.
Опыт –лучший учитель (Цицерон)
Современная физика содержит огромное количество теоретических сведений о нашем мире. Подавляющее большинство этих сведений получают из многочисленных экспериментов в результате их обобщения. В некоторых случаях роль проводимых экспериментов состоит только в подтверждении выдвинутых гипотез и предположений. В любом случае значимость физического опыта трудно переоценить, поскольку он, безусловно, является для нас единственным мерилом понимания окружающего мира.
В учебном процессе проведение опытов (выполнение лабораторных работ) является весьма важным элементом обучения, позволяющим лучше усвоить и запомнить основные законы природы, для дальнейшего осознанного использования полученных знаний на практике.
Выполнение описанных в пособии лабораторных работ по молекулярной физике и термодинамике позволяет глубже разобраться в ряде процессов, относящихся к газам и жидкостям.
Особенностью многих физических экспериментов в данном разделе физики является отсутствие возможности быстро и просто провести прямые измерения некоторых физических величин. К таким величинам, например, можно отнести показатель адиабаты, энтропию, вязкость, коэффициент теплопроводности и др. В этих случаях роль эксперимента усиливается, касаясь уже не только возможности прямого измерения исследуемых величин, но и выявление их физического смысла.
Данное пособие соответствует содержанию профессиональной программы по курсу «Общая физика» для инженерных специальностей технических вузов и состоит из теоретической части, позволяющей студентам найти ответы на контрольные вопросы, и экспериментальной части (лабораторных работ по молекулярной физике и термодинамике). В пособии имеется достаточно большое количество иллюстраций, обеспечивающих активное и прочное усвоение изложенного материала.
В приложении к основному тексту пособия приведены необходимые справочные данные.
5

1. Молекулярно-кинетическая теория идеальных газов
ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
М о л е к у л я р н а я ф и з и к а – это раздел физики, в котором изучают структуру, свойства и агрегатное состояние веществ, исходя из м о л е к у л я р - н о - к и н е т и ч е с к и х представлений об их природе. Согласно этим представлениям все вещества состоят из атомов, молекул или ионов, которые находятся
внепрерывном хаотическом тепловом движении.
Вмолекулярной физике используют два различных, но дополняющих друг друга метода: с т а т и с т и ч е с к и й и т е р м о д и н а м и ч е с к и й . Первый лежит в основе молекулярно-кинетической теории газов и основан на исполь-
зовании т е о р и и в е р о я т н о с т е й и представления изучаемого объекта в виде идеального газа . Все процессы, происходящие в макроскопической системе, и ее свойства объясняются как совокупный эффект от взаимодействия большого числа микрочастиц (атомов или молекул). Поэтому молекулярнокинетическую теорию называют еще и с т а т и с т и ч е с к о й ф и з и к о й .
Термодинамический метод, в отличие от статистического, не рассматривает внутреннее строение изучаемых объектов и не изучает характер движения отдельных микрочастиц. Он основан на анализе условий и закономерностей превращения различных видов энергии исследуемой системы при ее переходе из одного состояния в другое.
Прежде чем перейти к рассмотрению основ молекулярной физики необходимо дать несколько определений.
Т е р м о д и н а м и ч е с к а я с и с т е м а – это мысленно выделенная совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой так и с внешней средой.
С о с т о я н и е с и с т е м ы |
задается т е р м о д и н а м и ч е с к и м и п а р а - |
м е т р а м и ( п а р а м е т р а м и |
с о с т о я н и я ) – совокупностью физических |
величин, которые характеризуют свойства системы: удельный объем (v), давле-
ние (p), температура (Т).
У д е л ь н ы й о б ъ е м v это объем единицы массы, когда тело однородно, то есть его плотность = const:
v Vm 1 .
Поскольку при постоянной массе удельный объем пропорционален общему объему, то макроскопические свойства однородного тела можно характеризовать объемом тела.
Да в л е н и е м называется физическая величина
рdFdSn ,
6
где dFn – это модуль нормальной силы, действующий на малый участок поверхности тела.
Т е м п е р а т у р а – это физическая величина, |
характеризующая с о - |
с т о я н и е т е р м о д и н а м и ч е с к о г о р а в н о в е с и я |
макроскопической сис- |
темы. Под равновесным состоянием понимают такое состояние термодинамической системы, при котором термодинамические параметры не меняются во времени.
В соответствии с решением XI Генеральной конференции по мерам и весам с 1960 г. можно применять только д в е т е м п е р а т у р н ы е ш к а л ы – т е р м о д и н а м и ч е с к у ю и М е ж д у н а р о д н у ю п р а к т и ч е с к у ю , градуи-
рованные соответственно в Кельвинах (К) и в градусах Цельсия ( С). В международной практической шкале в качестве реперных точек принята температура замерзания и кипения воды при давлении 1,013 105 Па. Термодинамическая температурная шкала определяется по одной реперной точке – это тройная точка воды – температура, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии. Температура замерзания воды равна 273,15 К. Термодинамическая температура Т и температура по Международной практической шкале t связаны соотношением:
Т = 273,15 + t.
Температура Т = 0 называется н у л е м К е л ь в и н а . Н о р м а л ь н ы м и у с л о в и я м и (н.у.) принято считать температуру Т0 = 273,15 К и давление р0 = 1,013 105 Па.
Параметры состояния системы могут изменяться. Любое изменение в системе, связанное с изменением хотя бы одного из ее термодинамических па-
раметров, называют т е р м о д и н а м и ч е с к и м п р о ц е с с о м .
В молекулярной физике массы атомов и молекул принято характеризовать не их абсолютными значениями, например в кг, а относительными безраз-
мерными величинами а т о м н о й (Аr) и м о л е к у л я р н о й (Мr) м а с с а м и . В
качестве а т о м н о й е д и н и ц ы м а с с ы (а.е.м., mу) принимается 1/12 массы изотопа углерода 12С (mу = 1,66 10-27 кг). О т н о с и т е л ь н а я м о л е к у л я р н а я м а с с а Мг = m0/ mу, где m0 абсолютное значение массы молекулы.
В молекулярной физике также используется понятие к о л и ч е с т в а в е - щ е с т в а , которое выражается в м о л я х . М о л ь равен такому количеству вещества, которое содержит столько же структурных элементов (атомов, молекул), сколько атомов содержится в 0,012 кг изотопа углерода 12С. Следовательно, 1 моль любого вещества содержит одинаковое число структурных элементов, которое называется п о с т о я н н а я А в о г а д р о :
N A |
0,012 |
6,022 1023 |
1 |
. |
|
|
|||
|
12m y |
моль |
||
7
Например, N = 1025 молекул водорода и N = 1025 молекул кислорода яв-
ляются о д и н а к о в ы м и к о л и ч е с т в а м и в е щ е с т в а , хотя они имеют раз-
ные массы: 3,34 10-2 кг и 0,531 кг соответственно.
В молекулярной физике используют также понятие м о л я р н а я м а с с а, которая определяется как масса 1 моля вещества, то есть = NА m0.
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
Молекулярно-кинетическая теория описывает поведение и свойства особого идеального объекта, называемого и д е а л ь н ы м г а з о м . В основе данной физической модели лежит молекулярное строение вещества. Создание молекулярной теории связано с работами Р. Клаузиуса, Дж. Максвелла, Д. Джоуля
иЛ. Больцмана.
Ид е а л ь н ы й г а з . Молекулярно-кинетическая теория идеального газа строится на следующих посылках:
1)атомы и молекулы можно рассматривать как материальные точки, находящиеся в непрерывном движении;
2)собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
3)все атомы и молекулы являются различимыми, то есть существует принципиальная возможность следить за движением каждой частицы;
4)до столкновения молекул газа между ними отсутствуют силы взаимодействия, а соударения молекул между собой и со стенками сосуда предполагаются абсолютно упругими;
5)движение каждого атома или молекулы газа описывается законами класси-
ческой механики.
Законы, полученные для идеального газа можно использовать при изучении реальных газов. Для этого создают экспериментальные модели идеального газа, в которых свойства реального газа близки характеристикам идеального газа (например, при низких давлениях и высоких температурах).
ЗАКОНЫ ИДЕАЛЬНОГО ГАЗА
р
Т3 Т2 Т1
Т3
Т1 Т2
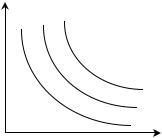
З а к о н Б о й л я - М а р и о т т а :
Для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоян-
ная: |
рV = const, |
(1.1) |
|
при T = const, m = const. |
|
V |
Кривая, изображающая зависимость |
Рис. 1.1. Зависимость давления р |
между величинами р и V, характеризует |
газа от объема V при постоян- |
свойства вещества при постоянной темпе- |
ной температуре Т = const |
ратуре, и называется и з о т е р м о й это |
|
8
гипербола (рис.1.1.), а процесс, протекающий при постоянной температуре, называется изотермическим.
За к о н ы Г е й - Л ю с с а к а :
1.Объем данной массы газа при постоянном давлении изменяется линейно с температурой
V = V0 (1 + t) при Р = const, m = const. |
(1.2) |
2.Давление данной массы газа при постоянном объеме изменяется линейно с температурой (закон Шарля ) :
|
|
|
p = p0 (1 + t) при V = const, |
m = const. |
(1.3) |
||||||||
В уравнениях (1.2) и (1.3) температура выражена по шкале Цельсия, дав- |
|||||||||||||
ление и объем – при 0 С, при этом |
1 |
|
|
1 |
. |
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
273,15 |
|
|
К |
|
|
|
||
|
|
V |
р2 = const |
|
|
|
|
|
|
р |
V2= const |
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
р1 =const |
|
|
|
|
|
|
|
|
V1=const |
-1/ |
0 |
t, C |
|
-1/ |
0 |
t, C |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1/ |
Т, К |
|
|
0 |
|
1/ |
Т, К |
|||||
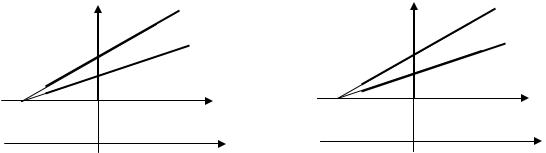
Рис. 1.2. Зависимость объема газа от |
Рис. 1.3. Зависимость давления газа от |
||||||||||||
|
температуры при постоян- |
|
|
|
|
температуры при постоянном |
|||||||
|
ном давлении, р2 р1 |
|
|
|
|
объеме, V2 V1 |
|
||||||
Процесс, протекающий при постоянном давлении, называется и з о б а р -
ны м , его можно представить в виде линейной функции (рис. 1.2.). Процесс, протекающий при постоянном объеме, называется и з о х о р -
ны м (рис. 1.3.).
Из уравнений (1.2) и (1.3) следует, что изобары и изохоры пересекают ось температур в точке t = 1/ = 273,15 С. Если перенести начало отсчета в эту точку, то перейдем к шкале Кельвина.
Вводя в формулы (1.2) и (1.3) термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид:
V = V0 (1+ t) = = V0 [1+ (T 1/ )] = =V0 T; p = p0 (1+ t) = p0 [1+ (T 1/ )] = p0 T;
9
V1 |
|
|
T1 |
|
при p = const, m = const; |
(1.4) |
||
V2 |
T2 |
|||||||
|
|
|
|
|
||||
p1 |
|
|
|
T1 |
|
при V = const, m = const, |
(1.5) |
|
p2 |
|
T2 |
|
|||||
|
|
|
|
|
||||
где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.
З а к о н А в о г а д р о :
моли любых газов при одних и тех же температурах и давлениях занимают одинаковые объемы.
При нормальных условиях этот объем равен V ,0 = 22,41 10-3 м3/моль. По определению, в одном моле различных веществ содержится одно и то же число молекул, равное п о с т о я н н о й А в о г а д р о : NA = 6,022 1023 моль-1.
З а к о н Д а л ь т о н а :
давление смеси разных идеальных газов равно сумме парциальных давлений р1, р2, р3 … рn, входящих в нее газов:
р = р1 + р2 + р3 + …+ рn.
П а р ц и а л ь н о е д а в л е н и е – это давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА (УРАВНЕНИЕ КЛАПЕЙРОНА-МЕНДЕЛЕЕВА)
Между температурой, объемом и давлением существует определенная связь. Эта связь может быть представлена функциональной зависимостью:
f (p, V, T) = 0.
В свою очередь каждая из переменных (р, V, T) является функцией двух других переменных. Вид функциональной зависимости для каждого фазового состояния вещества (твердого, жидкого, газообразного) отыскивается экспериментально. Это весьма трудоемкий процесс и уравнение состояния установлено лишь для газов, которые находятся в разреженном состоянии, и в приближенной форме – для некоторых сжатых газов. Для веществ, находящихся не в газообразном состоянии, эта задача до сих пор не решена.
Французский физик Б. Клапейрон вывел у р а в н е н и е с о с т о я н и я и д е а л ь н о г о г а з а , объединив законы Бойля-Мариотта, Гей-Люссака, Шарля:
pV |
B const . |
(1.6) |
|
T |
|||
|
|
Выражение (1.6) и есть уравнение Клапейрона, где В – газовая постоянная. Она различна для разных газов.
Д.И. Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (1.6) к одному молю и использовав молярный объем V . Со-
10
