Контрольные вопросы

1. Что такое работа выхода электрона из металла?

2. Какое явление называется термоэлектронной эмиссией?

3. Расскажите об устройстве трёхэлектродной лампы.

4. Что такое анодная и сеточная характеристики триода?

5. Назовите основные параметры триода, дайте их определения.

6. Как экспериментально получить основные параметры триода?

IV. Постоянное магнитное поле

4.1. Магнитное поле и его характеристики. Закон Ампера.

Опыт показывает, что, подобно тому, как в пространстве, окружающем электрические заряды возникает электрическое поле, в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, которое называется магнитным.

Источники магнитного поля:

1) проводники с током; 2) намагниченные тела; 3) переменное электрическое поле.

Идеальные модели:

1) движущийся электрический точечный заряд qV ( V – скорость);

2) Элемент тока Idl, где. dl – длина участка проводника, направление которого совпадает с направлением тока.

Силовая характеристика магнитного поля В – вектор магнитной индукции. Помещенный в какую-либо точку поля «пробный» элемент тока Idl испытывает действие силы:

dF = [Idl, B]. (4.1) В скалярной форме dF = Idl B sinα.

Если α = π/2, т.е. Idl перпендикулярно вектору В, а значит dF максимальна. Таким образом:

– (4.2)

определение силовой характеристики магнитного поля В. Единица магнитной индукции – Тесла: 1 Тл = 1 Н/(А∙м).

Формула (4.1) – закон Ампера, dF – сила Ампера.

Если В = const – поле однородное. Направление dF находится по правилу векторного произведения – правилу левой руки (правило буравчика) (рис.4.1).

Магнитная сила dF не является центральной, т.е. не является консервативной.

Графически магнитное поле изображается в виде линий В – силовых линий магнитного поля (рис. 4.2). Это такие линии, которые проводятся так, что вектор В в каждой точке силовой линии направлен по касательной к ней. Направление силовых линий и вектора В определяется по правилу буравчика.

Л инии В не имеют начала и конца, так как не существует магнитных зарядов.

Линии В либо замкнуты, либо идут из ∞ в ∞, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя ее, но никогда не возвращаясь вторично в любую точку поверхности.

4.2. Поле точечного заряда, движущегося с V=const и V<< c

(Нерелятивистский случай)

Этот закон получен из экспериментальных данных:

, (4.3)

г де r – радиус-вектор, проведенный от заряда q к точке наблюдения, µ₀ – магнитная постоянная = 4π^.10^-7 Гн/м.

Закон (4.3) в скалярном виде:

,

где α – угол между векторами V и В.

4 .3. Закон Био-Савара-Лапласа

В соответствии с законом Био-Савара-Лапласа магнитная индукция поля, создаваемого элементом проводника с током в точке пространства, удаленной от этого элемента проводника на расстояние (рис. 4.3) равна:

, (4.4)

Формула (4.4) в скалярной форме:

,

где α – угол между векторами и . Направление вектора можно определить по правилу правого винта.

Закон Био-Савара-Лапласа позволяет найти индукцию магнитного поля в данной точке пространства от любой системы проводников с током. Для этого нужно воспользоваться принципом суперпозиции:

B = ∑B_i или B = ∫dB. (4.5)

Наиболее просто интеграл (4.5) вычисляется, если все векторы коллинеарные (индукция магнитного поля от прямолинейного проводника или на оси кругового проводника с током).

Определим магнитную индукцию на оси витка с током на расстоянии Х от центра контура (рис. 4.4).

К аждый элемент тока создает индукцию . Векторы перпендикулярны к плоскостям, проходящим через соответствующий элемент и точку, в которой определяем поле. Следовательно, он и образует симметричный конический веер. Из соображений симметрии можно заключить, что результирующий вектор В направлен вдоль оси контура. Каждый из составляющих векторов вносит в результирующий вектора вклад , равный по модулю

, (4.6)

где R – радиус витка с током. Угол α между векторами и – прямой.

Поэтому результирующая индукция магнитного поля равна по модулю:

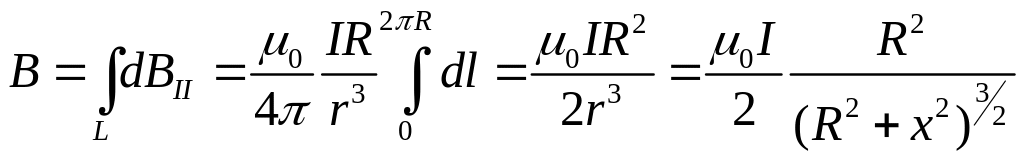. (4.7)

Здесь использовано, что . В центре кругового тока (х = 0) магнитная индукция равна

. (4.8)