2.2. Закон Ома в дифференциальной форме с точки зрения классической теории проводимости металлов (ктпм)

Создатели классической электронной теории проводимости – Друдэ и Лоренц. Согласно этой теории высокая электропроводность металлов объясняется:

1) наличием громадного количества свободных электронов;

2) движение электронов подчиняется законам классической механики Ньютона;

3) в этой теории пренебрегают взаимодействием электронов между собой, а взаимодействие электронов с положительными ионами сводят только к соударениям.

Таким образом, электроны проводимости в теории Друдэ-Лоренца рассматриваются как электронный газ, обладающий свойствами одноатомного идеального газа.

j = ne‹V›. (2.1)

На каждый электрон действует сила F = eE, которая сообщает ему ускорение: F = ma = .

Скорость электрона изменяется от 0 до V_max. Тогда средняя скорость дрейфа электрона: – среднее время свободного пробега электрона (т.е. среднее время между двумя последовательными соударениями).

1/γ = ρ – удельное сопротивление проводника. Таким образом, получаем

–

это закон Ома в дифференциальной форме: плотность тока проводимости j равна произведению удельной электропроводности проводника на напряженность электрического поля в проводнике.

Вектора j и Е имеют одинаковое направление.

2.3. Обобщенный закон Ома

Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей тока приведет очень быстро к тому, что напряженность внутри проводника станет равной нулю и ток прекратится. Таким образом, при наличии лишь кулоновских сил невозможно поддерживать в цепи электрический ток. Следовательно, для поддержания в цепи постоянного тока необходимо, чтобы на носители тока действовали помимо кулоновских сил иные силы, не электростатического происхождения, называемые сторонними.

Если кулоновские силы вызывают соединение разноименных зарядов, выравнивание потенциала и исчезновение поля в проводнике, то сторонние силы, наоборот вызывают разделение разноименных зарядов и поддерживают разность потенциалов на концах проводника. Сторонние силы действуют на носители тока внутри источников электрической энергии (гальванических элементов, аккумуляторов, электрических генераторов и т.п.).

В общем случае, на носитель тока q, действует сила:

где – напряженность поля кулоновских сил, – напряженность поля сторонних сил. Тогда

Умножим скалярно обе части равенства на dl. |dl | – длина элемента проводника. Вектор dl направлен по току.

Интегрируем данное выражение по длине участка цепи 1-2:

электродвижущая сила (ЭДС), действующая на участке 1-2.

–

ЭДС численно равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда.

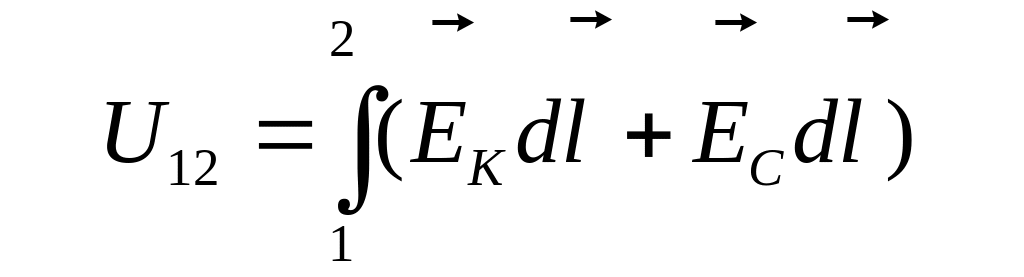– напряжение на участке цепи 1-2.

Напряжение – это физическая величина, численно равная суммарной работе, совершаемой кулоновскими и сторонними силами при перемещении по участку 1-2 единичного положительного заряда. Таким образом,

U₁₂ = (φ₁ – φ₂) + ε₁₂.

Сопротивление на участке 1-2: