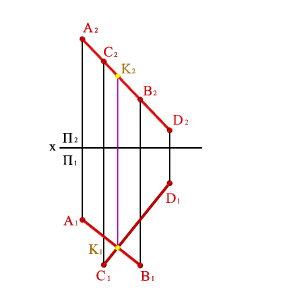- •Матрицы: определение и свойства.
- •Определители: свойства, определители 1го и 2го порядков
- •Вычисление определителей высших порядков
- •5. Метод приведения к треугольному виду.
- •6. Формула для ведущих элементов.
- •Системы линейных уравнений, методы их решения (Крамера, Гаусса, матричный)
- •Векторы, действия с векторами, скалярное произведение векторов, лз и лнз векторы
- •Векторное и смешанное произведения векторов
- •Линейное векторное пространство: определение, свойства.
- •Базис линейного векторного пространства, переход от одного базиса к другому
- •Линейные операторы, матрица линейного оператора
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы: определения, свойства, теоремы.
- •Прямая на плоскости, способы задания
- •1.Двумя точками (а и в).
- •2. Двумя плоскостями (a; b).
- •3. Двумя проекциями.
- •2. Для построения фронтального следа n прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.
- •13. Расположение прямой на плоскости
- •14. Кривые второго порядка
- •Окружность
- •Гипербола
- •15. Способы задания и расположение плоскости в пространстве
- •16. Способы задания прямой в пространстве Векторно-параметрическое уравнение прямой
- •17. Основные задачи в пространстве: углы, условие параллельности и перпендикулярности
- •18. Основные задачи в пространстве: расстояния, взаимное расположение двух прямых
- •19. Поверхности второго порядка
- •20. Задачи линейного программирования, экономическая модель
- •Экономическая модель задачи
- •21. Основы мат. Моделирования, мат. Модель задачи линейного программирования
- •Пример составления математической модели
- •22. Задача оптимального распределения ресурсов
- •Конкретная ситуация парис (Планирование и Анализ Рационального Использования Средств)
- •Построение математической модели
- •Общий вид задачи оптимального распределения ресурсов
- •Варианты задачи оптимального распределения ресурсов
- •Верхняя и нижняя граница плана
- •Комплектность выпуска
- •Изменение ресурсной обеспеченности
- •Динамическое планирование
- •23. Общая задача линейного программирования
- •Область допустимых планов. Оптимальный план и оптимум
- •Область допустимых планов
- •Оптимальный план и оптимум
- •Условия разрешимости задачи и единственности решения.
- •Построение области допустимых планов
- •Построение градиента и определение оптимального плана
- •24. Основные теоремы линейного программирования.
- •25. Графический метод решения задачи линейного программирования
- •26. Симплекс-метод
- •27. Прямая и двойственная задача линейного программирования. Геометрическая интерпретация двойственной задачи
- •28. Транспортная задача Общий вид транспортной задачи
- •Пример транспортной задачи
- •29. Нелинейное программирование
2. Для построения фронтального следа n прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.
|
|
|
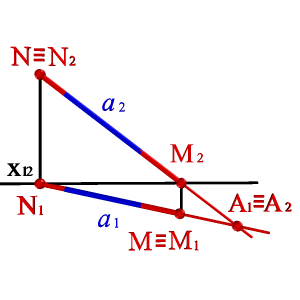
С помощью этих правил найдены на эпюре следы прямой а (рис.27) . Здесь же показаны совпавшие проекции точки А, принадлежащей рассматриваемой прямой. Особенность этой точки в том, что она равноудалена от плоскостей проекций, то есть находятся в биссекторной плоскости S2бис. Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.
|
|
|
|---|---|---|---|---|---|
|
Рисунок 27. Нахождение горизонтального и фронтального следов прямой линии |
|
|||
Взаимное расположение точки и прямой |
|
||||
Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 28 точек, только одна точка С лежит на прямой АВ.
|
б)
модель |
Рисунок 28. Взаимное расположение точки и прямой |
|
В тех случаях, когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П1, П2 и П3), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П1, П2 или П3. Например, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости проекций (рис.29).
|
|
|
|
а) эпюр |
б) модель |
||
Рисунок 29. Точка и прямая, расположенные в профильной плоскости уровня |
|||
Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении.
Зная это условие можно определить принадлежность точки К прямой АВ:
А2К2 /К2В2 ¹А1К1/К1В1 Þ КÏАВ
Взаимное расположение двух прямых |
|
Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.
1. Параллельные прямые линии.
Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.
Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если AB//CD то A1B1//C1D1; A2B2//C2D2; A3B3//C3D3 (рис.33). В общем случае справедливо и обратное утверждение.
|
б)
эпюр |
Рисунок 33. Параллельные прямые |
|
Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис. 34). В рассмотренном случае проекции отрезков на плоскость П3 пересекаются, следовательно, они не параллельны.
Решение этого вопроса можно получить сравнением двух соотношений если:
А2В2/ А1В1= С2Д2/ С1 Д1Þ АВ//СД
А2В2/ А1В1¹ С2Д2/ С1Д1Þ АВ#СД
|
|
|
|
а) модель |
б) эпюр |
||
Рисунок 34. Прямые параллельные профильной плоскости проекций |
|||
2. Пересекающиеся прямые.
Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.
Если
прямые пересекаются, то точки пересечения
их одноименных проекций находится на
одной линии связи
(рис.
35).


|
|
|
|
а) модель |
б) эпюр |
||
Рисунок 35. Пересекающиеся прямые |
|||
В общем случае справедливо и обратное утверждение, но есть два частных случая:
1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например, профильной (рис.36), то по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, однако сами отрезки не пересекаются, потому что точка пересечения профильных проекций этих отрезков не лежит на одной линии связи с точками пересечения их горизонтальной и фронтальной проекций.
|
б)
эпюр |
Рисунок 36. Одна из прямых параллельна профильной плоскости проекций |
|
2. Пересекающие прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций (рис. 37).
О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции (А1В1∩С1D1Þ АВ∩СD).
|
|
|
|
а) модель |
б) эпюр |
||
Рисунок 37. Пересекающиеся прямые расположены в фронтально проецирующей плоскости |
|||
3. Скрещивающиеся прямые
Скрещивающимися называются две прямые не лежащие в одной плоскости.
Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.
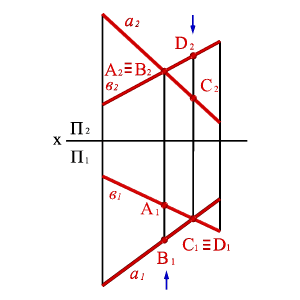
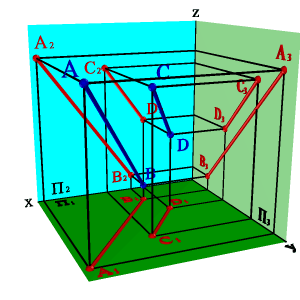
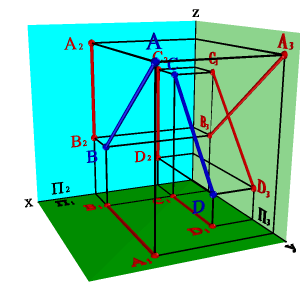
Точке пересечения фронтальных проекций прямых (рис. 38) соответствуют две точки А и В, из которых одна принадлежит прямой а, другая в. Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки А и В находятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точка В, лежащая на прямой в, следовательно, прямая в проходит в этом месте ближе прямой а и фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и D решение аналогично).
Этот способ определения видимости по конкурирующим точкам. В данном случае точки А и В- фронтально конкурирующие, а С и D -горизонтально конкурирующие.
|
|
|
|
а) модель |
б) эпюр |
||
Рисунок 38. Скрещивающиеся прямые |
|||

 а)
эпюр
а)
эпюр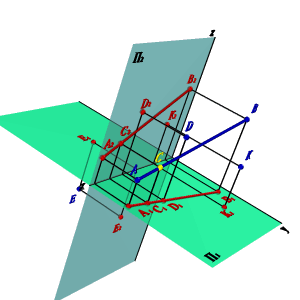


 а)
модель
а)
модель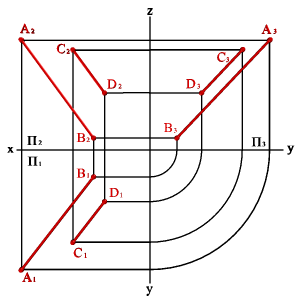

 а)
модель
а)
модель