Собственные векторы и собственные значения линейного оператора
Пусть А: Xn → Xn — линейный оператор.
Вещественное число λ называется собственным значением оператора А, если существует ненулевой вектор x О Xn такой, что
А (x) = λ (x). |
Вектор x называется собственным вектором оператора А, соответствующим собственному значению λ .
Замечание. Из определения следует, что образ собственного вектора коллинеарен его прообразу.
Свойства собственных векторов:
Пусть А: Xn → Xn — линейный оператор.
-Все собственные векторы линейного оператора, соответствующие одному и тому же собственному значению, вместе с нулевым вектором образуют линейное пространство.
-Собственные векторы линейного оператора, соответствующие различным собственным значениям, линейно независимы.
-Если линейный оператор А: Xn → Xn имеет n различных (вещественных) собственных значений, то собственные векторы, соответствующие этим собственным значениям, образуют базис в Xn . Такой базис называется собственным базисом линейного оператора А.
-Матрица A линейного оператора А: Xn → Xn в некотором базисе x1, x2, … , xn имеет диагональный вид тогда и только тогда, когда этот базис собственный, причем диагональные элементы этой матрицы — собственные значения оператора λ1, λ2, … , λn .
Нахождение собственных значений и собственных векторов по матрице оператора
Теорема. Вещественное число λ является собственным значением линейного оператора А: Xn → Xn тогда и только тогда, когда λ удовлетворяет уравнению
|
det (A − λE) = 0, |
(1) |
где A — квадратная матрица n –го порядка — матрица оператора А в некотором базисе, а E — единичная матрица того же порядка, что и A .
Доказательство. Пусть вектор x — собственный вектор оператора А, соответствующий собственному значению λ , т.е. по определению
А(x) = λ(x), А(x )= λ Е(x), (А− λ Е) x = θ. |
Следовательно, чтобы найти собственные значения и собственные векторы оператора А, нужно решить однородную систему n линейных уравнений с n неизвестными (A − λE)X = O .
Так как по определению собственного вектора x ≠ θ , то нас интересуют лишь нетривиальные решения этой системы уравнений. Необходимым и достаточным условием нетривиальной совместности однородной системы n уравнений с n неизвестными является условие det (A − λE) = 0 , что и требовалось доказать.
Уравнение (1) называется характеристическим уравнением оператора А.
Т1: Если матрица лин. оператора в некотором базисе имеет диагональный вид, то все векторы этого базиса являются собственными векторами лин. оператора, а числа на главной диагонали являются собственными значениями.
Т2: Если лин. оператор имеет n различных собственных значений, то все его собственные векторы линейно независимы и матрица лин. оператора в этом базисе имеет диагональный вид.
Собственные значения и векторы не зависят от базиса.
Квадратичные формы: определения, свойства, теоремы.
Определение.
Квадратичной формой
переменных
,принимающих
числовые значения , называется числовая
функция вида
,
где
-
числа, называемые коэффициентами
квадратичной формы.( квадратичная форма
- в n-мерном
пространстве L(x1,x2,…xn)-сумма,
каждое слагаемое которой либо квадрат
одной из переменных, либо произведение
двух различных переменных, взятых с
коэффициентом)
Определение.
Матрицей квадратичной формы
переменных
,
называется симметрическая матрица
порядка
,
элементы главной диагонали которой
совпадают с коэффициентами при квадратах
переменных, а каждый недиагональный
элемент, расположенный в
ой
строке
ом
столбце, равен половине коэфициента
при
в
квадратичной форме.
Определение.
Рангом квадратичной формы называется
ранг её матрицы. Квадратичная форма
может быть записана в матричном виде
где
матрица
квадратичной формы и
.
Определение.
Квадратичная форма называется канонической
(имеет канонический вид), если коэфициенты
при
,
то есть, если матрица квадратичной формы
диагональная и следовательно
.,
где не все
коэффициенты
равны нулю.
Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.
Определение.
Нормальным видом квадратичной формы
называется такой канонический вид, в
котором коэффициенты при квадратах
неизвестных (не считая нулевых) равны
.
Определение.
Квадратичная форма
называется
положительно
(отрицательно)
определённой, если
при
всех
и
положительно (отрицательно)
полуопределённой,если
при
всех
.
Теорема (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определённой, необходимо и достаточно чтобы все угловые миноры матрицы квадратичной формы были положительны, то есть, чтобы
Здесь
-угловые
миноры матрицы квадратичной формы.
Следствие.
Для того чтобы квадратичная форма
была
отрицательно определённой, необходимо
и достаточно, чтобы знаки угловых миноров
матрицы квадратичной формы чередовались
следующим образом:
Определение квадратичной формы
Квадратичная
форма переменных
-
функция
-
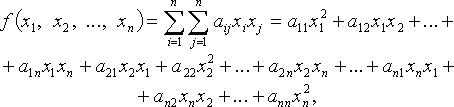
коэффициенты квадратичной формы. Без
ограничения общности считают
тогда
Если
переменные
принимают
действительные значения и
квадратичная
форма называется действительной.
Матричная запись квадратичной формы
Матрица
называется
матрицей квадратичной формы, ее ранг -
рангом квадратичной формы. Квадратичная
форма называется невырожденной, если
Главные миноры матрицы A называются главными минорами квадратичной формы.
В
пространстве
квадратичную
форму можно записать в виде
где
X
- координатный столбец вектора
В
пространстве
квадаратичную
форму можно представить в виде
где
f
- линейный самосопряженный оператор,
матрица которого в некотором
ортонормированном базисе равна A.
Канонический вид квадратичной формы
Квадратичная
форма называется канонической, если
все
т.
е.
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.
1. Ортогональное преобразование пространства :
где
-
собственные значения матрицы A.
2.
Метод Лагранжа - последовательное
выделение полных квадратов. Например,
если
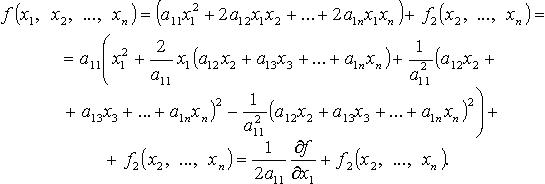
Затем
подобную процедуру проделывают с
квадратичной формой
и
т. д. Если в квадратичной форме все
но
есть
то
после предварительного преобразования
дело сводится к рассмотренной процедуре.
Так, если, например,
то
полагаем
3.
Метод Якоби (в случае, когда все главные
миноры
квадратичной
формы отличны от нуля):
Нормальный вид квадратичной формы
Для действительной квадратичной формы
где
r
= rank A.
Для комплексной квадратичной формы
r
= rank A.
Для действительных квадратичных форм имеет место закон инерции квадратичных форм: число положительных и число отрицательных квадратов в нормальном виде квадратичной формы не зависит от способа приведения квадратичной формы к нормальному виду с помощью невырожденных линейных преобразований.
Классификация действительных квадратичных форм Положительно-определенные
Квадратичные
формы, для которых
таких,
что
Нормальный
вид
Квадратичная
форма является положительно-определенной
тогда и только тогда, когда все ее главные
миноры положительны
(критерий
Сильвестра).
Отрицательно-определенные
Квадратичные
формы, для которых
таких,
что
Нормальный
вид
Квадратичная
форма является отрицательно-определенной
тогда и только тогда, когда
Положительно-полуопределенные
Квадратичные
формы, для которых
таких,
что
Нормальный
вид
r
< n,
r
= rank A.
Отрицательно-полуопределенные
Квадратичные
формы, для которых
таких,
что
Нормальный
вид
r
< n,
r
= rank A.
Неопределенные
Квадратичные
формы, которые принимают как положительные,
так и отрицательные значения. Нормальный
вид:
r
= rank A.