28. Транспортная задача Общий вид транспортной задачи

В общем случае имеется m пунктов производства и n пунктов потребления. Пункты производства пронумеруем числами от 1 до m. Номер пункта производства будем обозначать буквой i (таким образом, 1 £ i £ m). Пункты потребления пронумеруем числами от 1 до n. Номер пункта потребления будем обозначать буквой j (таким образом, 1£ j £ n). Рассмотрим некоторый период времени (например, месяц). Пусть a_i - объем производства за период времени в i-м пункте производства, b_i - количество продукции, требуемое за период времени в j-м пункте потребления. Пусть c_ij - стоимость перевозки единицы груза из i-го пункта производства в j-й пункт потребления.

Требуется определить план перевозок, удовлетворяющий условиям по пунктам производства и потребления и соответствующий наименьшим затратам на перевозки.

Для построения математической модели следует ввести переменные. Для каждой пары поставщик-потребитель, то есть для каждой пары (i,j) введем переменную х_ij - объем перевозки от пункта производства i к пункту потребления j.

Математическая модель транспортной задачи записывается следующим образом

 

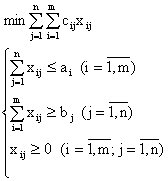
Целевая функция модели представляет собой общую стоимость всех перевозок. Она записана в виде двойной суммы. Внутренняя сумма соответствует пунктам производства, внешняя - пунктам потребления. Разумеется, эти знаки суммирования в целевой функции можно поменять местами. От перегруппировки слагаемых сумма не изменяется.

В модели указано, что целевую функцию следует минимизировать. Таким образом, модель предписывает искать план перевозок наименьшей общей стоимости.

В системе ограничений представлены три группы неравенств. В первой группе m неравенств, соответствующих пунктам производства. Каждое неравенство утверждает, что из соответствующего пункта не может быть вывезено больше, чем в нем имеется. Во второй группе n неравенств, соответствующих пунктам потребления. Каждое из них требует, чтобы в соответствующий пункт было привезено не меньше, чем требуется. В третьей группе m ´ n неравенств, обеспечивающих неотрицательность объема перевозок.

Представленная модель транспортной задачи с ограничениями-неравенствами называется открытой моделью. Задача разрешима в том и только в том случае, когда общий объем груза у поставщиков не меньше суммарной потребности потребителей, то есть когда выполнено неравенство:

.

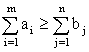Если выполнено обратное неравенство, то есть если

,

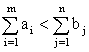то задача неразрешима, для нее не существует не только оптимального, но даже и допустимого плана.

Если общий объем груза у поставщиков в точности равен общей потребности потребителей, то есть если имеет место равенство:

,

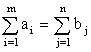то указанная выше открытая модель эквивалентна более простой закрытой модели, в которой основные неравенства заменены равенствами. Закрытая модель имеет следующий вид:

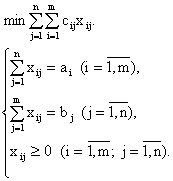
Пример транспортной задачи

Имеется два пункта производства продукции: "Северный" и "Южный". Эти пункты способны производить ежемесячно 1,5 тыс. тонн и 2 тыс. тонн продукции соответственно.

Имеется три пункта потребления этой продукции: "Горный", "Озерный" и "Лесной". Ежемесячные потребности этих пунктов в продукции составляют соответственно 0,8 тыс. тонн, 1,6 тыс. тонн и 1 тыс. тонн. Стоимость транспортирования 1 тонны груза от пункта производства к пункту потребления представлена в таблице 2.

Требуется построить математическую модель для определения такого плана перевозки грузов, с которым были бы связаны наименьшие затраты на перевозку.

Для удобства записи обозначим пункты производства числами 1 и 2 и пункты потребления числами 1, 2 и 3. Построение модели начнем с введения переменных. Обозначим посредством х_ij объем перевозки (в тоннах) от i-го пункта производства к j-му пункту потребления.

Индекс i принимает одно из двух значений 1 или 2, а индекс j - одно из трех значений 1, 2 или 3. Таким образом, мы ввели 6 переменных. Из них, например, переменная х₁₁ соответствует объему перевозок от 1-го пункта производства ("Северный") к 1-му пункту потребления ("Горный"), а переменная х₂₃ - объему перевозок от 2-го пункта производства ("Южный") к 3-му пункту потребления ("Лесной").

Табл. 1.6

Пункт назначения Пункт отправления	1. "Горный"	2. "Озерный"	3. "Лесной"
1. Северный	90	80	50
2. Южный	100	120	110

Набор значений переменных х_ij - это и есть план перевозок. Поскольку переменные имеют по два индекса, то план удобнее записывать не в виде вектора, а в виде матрицы:

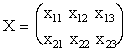
Математическая модель задачи записывается в следующем виде.

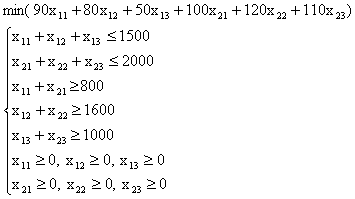
Целевая функция задачи представляет собой сумму произведений стоимостей перевозки 1 т груза на объем перевозки для каждой пары поставщика-потребителя, то есть общую суммарную стоимость всех перевозок, соответствующих плану Х. Эту суммарную стоимость следует минимизировать при условии, что будут выполнены все ограничения.

Ограничения на перевозки можно разбить на три группы. Первая группа - это верхние два неравенства. В каждое из них входят переменные с одним и тем же первым индексом, но различными вторыми индексами, то есть переменные, соответствующие одному и тому же пункту производства, но различным пунктам потребления. Каждое из этих неравенств говорит о том, что суммарный объем всех грузов, вывозимых из одного и того же пункта производства в разные пункты потребления, не превосходит того количества продукции, которое может быть произведено в данном пункте производства.

Вторая группа - это следующие три неравенства. В каждое из них входят переменные с одним и тем же вторым индексом, но разными первыми индексами. Эти переменные соответствуют одному пункту потребления, но разным пунктам производства. Такое неравенство утверждает, что объем всего груза, который свозится из разных пунктов производства в один и тот же пункт потребления, должен быть не меньше, чем объем потребности в данном пункте потребления.

Наконец, третья группа ограничений утверждает, что все объемы перевозок неотрицательны.

В данной задаче сумма грузов, имеющихся во всех пунктах производства (3500 т) больше, чем сумма потребностей в грузах, имеющихся во всех пунктах потребления (3400 т). Такая транспортная задача имеет оптимальный план перевозок. Как найти такой оптимальный план - этим вопросом мы займемся позже, но такой план существует. А вот если бы оказалось наоборот, если бы суммарный груз в пунктах производства оказался меньше суммарной потребности в пунктах потребления, то задача оказалась бы неразрешимой. Она не имела бы даже допустимых планов, и тем более не имела бы оптимального.

 Если же суммарный груз в пунктах производства в точности равен суммарной потребности в пунктах потребления, то задача имеет решение, и ее математическая модель в этом случае может быть приведена к более удобной форме.

В этом случае из пунктов производства должно быть вывезено все. Это значит, что ограничения первой группы, связанные с пунктами производства, должны выполняться в форме равенства. Точно так же и пункты потребления не могут быть в этом случае удовлетворены с избытком. Следовательно, и ограничения второй группы должны выполнятся в форме равенства.

Таким образом, если, например, потребность третьего пункта потребления равна не 1000 т, а 1100 т, так что суммарный груз в пунктах производства (3500 т) равен суммарной потребности в пунктах потребления (тоже 3500 т), то в математической модели неравенства первых двух групп ограничений могут быть заменены равенствами. Модель в этом случае будет иметь следующий вид.

 

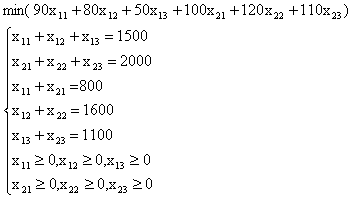
Неравенства, связанные с пунктами производства и потребления, заменены здесь равенствами. Модель транспортной задачи с ограничениями-неравенствами называется открытой моделью. Модель с ограничениями-равенствами носит название закрытой модели.