Определители: свойства, определители 1го и 2го порядков
Определитель n-ого порядка.
Определителем квадратной матрицы порядка n называется число:
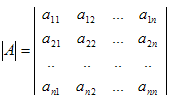
Свойства определителей:
Определитель транспонированной матрицы равен определителю исходной матрицы.
Если в определителе какие-либо две строки (столбца) равны между собой, то такой определитель равен 0.
Общий множитель всех элементов какой-либо строки (или столбца) можно выносить за знак определителя.
Если поменять в определителе местами какие-либо две строки (столбца), то определитель меняет знак.
Если все элементы какой-либо строки (столбца) определителя равны 0, то такой определитель равен 0.
Если к элементам какой-либо строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца) этого же определителя, умноженные на одно и то же число, то определитель не изменяется.
Миноры, алгебраические дополнения матрицы.
Минором Mij, соответствующим данному элементу определителя 3 порядка, называется определитель второго порядка, полученный из матрицы вычеркиванием i-ой строки и j-го столбца. Тогда формулу для вычисления определителя 3 порядка можно переписать в виде:
Если элементы матрицы отметить точками, то получим правило треугольников:
(+) |
(-) |
|
|
Слагаемые со знаком плюс представляют собой произведение элементов определителя, взятых по три так, как указано линией на левой части рисунка, а со знаком минус - на правой части.
Алгебраическим
дополнением элемента 
определителя
3-го порядка называется его минор, взятый
со знаком плюс, если (i+j) - четное число,
и со знаком минус, если (i+j) - нечетное
число, т.е.
Определители являются основными числовыми характеристиками квадратных матриц. Порядок квадратной матрицы определяет порядок определителя.
Определителем
(детерминантом) матрицы
,
состоящей
из одного числа
,
называется само это число.
Определителем
матрицы А= 
второго
порядка называется число, равное разности
произведений элементов главной и
побочной диагоналей:
Вычисление определителей высших порядков
Рассмотрим матрицу третьего порядка:
Определителем матрицы A третьего порядка называется число
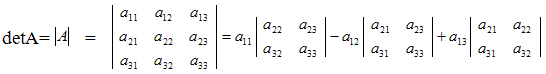
Данная формула называется формулой разложения определителя 3 порядка по элементам первой строки.
Формулы для определителя
1. Определитель треугольной матрицы равен произведению элементов ее главной диагонали.
2.Если
матрица
невырожденная,
то
и
(произведение
ведущих элементов).
Знак
плюс или минус дается определителем
матрицы
(или
)
и зависит от того, является число
перестановок строк в приведении четным
или нечетным. Для треугольных сомножителей
имеем
и
3. Теорема Лапласа (метод понижения порядка): определитель матрицы может быть вычислен разложением по алгебраическим дополнениям i-й строки(столбца):
.
Алгебраическое
дополнение
есть
определитель подматрицы
,
взятый с нужным знаком:
.
Подматрица образуется вычеркиванием i-й строки и j-го столбца матрицы .
4.
Правило
Крамера:
j-й элемент вектора
равен
,
где
В
-
вектор
заменяет
собой j-й столбец матрицы
.