Коэффициент корреляции
Коэффициентом
корреляции
случайных величин x
и y
называют отношение корреляционного
момента к произведению средних
квадратических отклонений этих величин:
Для независимых и коэффициент корреляции равен нулю.
Свойства коэффициента корреляции
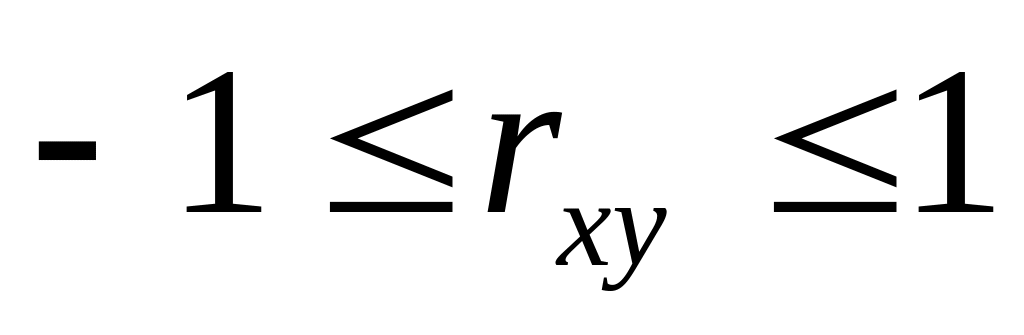
Если
,
то
,
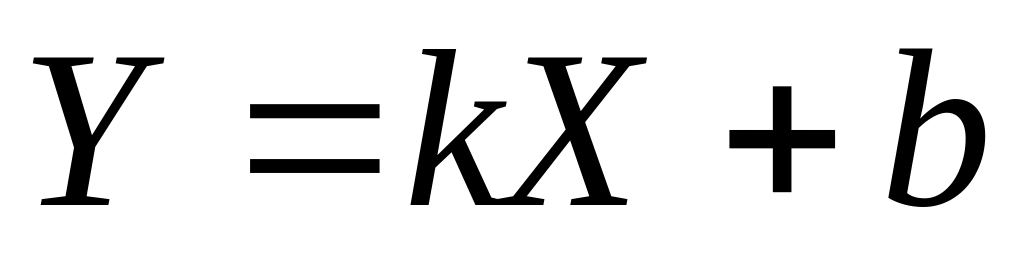где k и b — константы, k>0.Если,
,
то
,
где k<0.
Коэффициент корреляции достигает своих предельных значений –1 и 1 в том и только в том случае, если между и имеется линейная зависимость.
При
<1
линейная зависимость отсутствует, хотя
по мере приближения
к единице совместное распределение
,
имеет тенденцию концентрироваться
вблизи некоторой прямой линии и величину
можно считать мерой близости к полной
линейной зависимости между
и
.
Введем понятие корреляционной зависимости между и . Две случайные величины называют коррелированными, если их ковариация или коэффициент корреляции отличны от нуля, и некоррелированными в противном случае.
Говорят, что между и существует прямая корреляционная зависимость, если с ростом случайная величина имеет тенденцию возрастать (при больших с большей вероятностью встречаются большие значения ). Если с ростом случайная величина имеет тенденцию убывать, говорят, что между и существует обратная корреляционная зависимость.
Чем
ближе
к единице, тем теснее глубина корреляционной
зависимости.
Пример: Найти коэффициент корреляции между величинами X и Y, совместный закон распределения которых задан следующей таблицей
-
1
2
3
4
10
0,2
0,02
0,01
0
0,23
20
0,03
0,3
0,02
0
0,35
30
0,02
0,1
0,2
0,1
0,42
0,25
0,42
0,23
0,1
1
Находим:
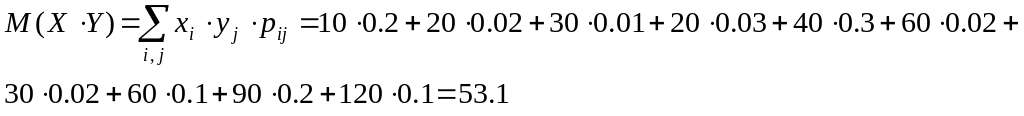
Аналогично,
найдем
и по ним
.
Окончательно получим
Лекция 11. Предельные теоремы теории вероятностей.
Несмотря на то, что заранее нельзя предсказать, какое из возможных значений примет случайная величина в результате опыта, при некоторых условиях суммарное поведение достаточно большого числа случайных величин становится закономерным. Иными словами, при очень большом числе случайных явлений их средний результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.
Для практики очень важно знание условий, при выполнении которых это может происходить. Эти условия указываются в теоремах, носящих общее название закона больших чисел, важнейшей из которых является теорема Чебышева. Для доказательства теоремы Чебышева используется неравенство Чебышева, которое мы сейчас рассмотрим.
Неравенство Чебышева
Вероятность
того, что отклонение случайной величины
X от ее математического ожидания по
абсолютной величине меньше положительного
числа ,
не меньше, чем
,
т.е.
Пример.
Номинальное значение диаметра втулки равно 5 мм, а дисперсия, из-за погрешностей изготовления, не превосходит 0,01. Оценить вероятность того, что размер втулки будет отличаться от номинала не более чем на 0,5 мм.
Решение:
По неравенству Чебышева
Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. Например, если мы захотим выяснить, какова вероятность того, что случайная величина X отклонится от своего математического ожидания не меньше, чем на 3 среднеквадратических отклонения, то неравенство Чебышева даст нам верхнюю границу этого значения 1/9 0,111. В то же время, например для нормального распределения вероятность такого отклонения намного меньше - 0,0027 (правило трех сигм).