Гипергеометрическое распределение (урновая схема)

Дискретная случайная величина имеет гипергеометрическое распределение, если она принимает значения с вероятностями

представляет вероятность выбора объектов, обладающих заданным свойством, из множества объектов, случайно извлеченных (без возврата) из совокупности объектов, среди которых объектов обладают заданным свойством. Ниже приведен пример графика гипергеометрического распределения.

Математическое ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение с параметрами равны:

Пример. Имеется 5 фирм, у трех из которых отчетность оформлена неправильно. 2 ревизора проверяют 2 произвольно выбранные фирмы. Какова вероятность того, что при проверке будет обнаружена неправильная отчетность а) ни в одной, б) в одной, в) в двух фирмах?

Решение. Данная задача может быть решена с помощью гипергеометрического распределения. По условию задачи общее число объектов (фирм) равно N = 10, число фирм с неправильной отчетностью M=3. Проверяется всего две фирмы (n =2). Число фирм с неправильной отчетностью среди двух выбранных – величина переменная (m=0, 1, 2). Таким образом, имеем

а) 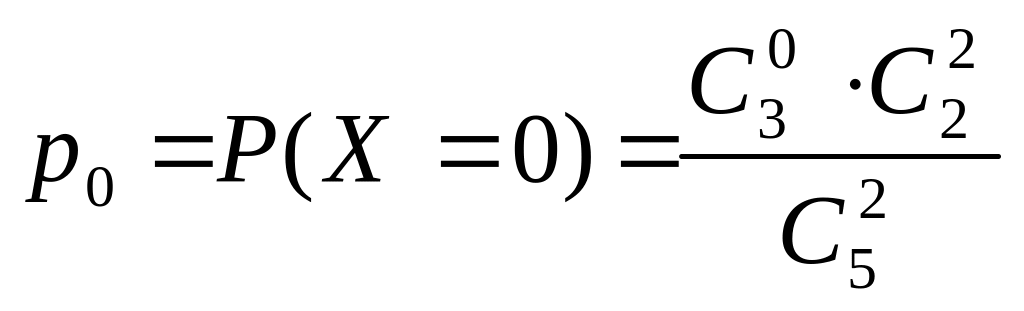(ни одной неправильной отчетности)

б) (одна неправильная отчетность)

в) (две неправильные отчетности).

Равномерное распределение.

Непрерывная случайная величина считается равномерно распределенной на отрезке (a,b), если ее плотность вероятности имеет вид:

График плотности вероятности для равномерного распределения

Математическое ожидание и дисперсия непрерывной случайной величины, имеющей равномерное распределение, равны соответственно:

Пример. Интервал движения автобуса равен 15 мин. Какова вероятность того, что пассажир на остановке будет ждать автобус не более 5 минут?

Решение. Пусть случайная величина - время ожидания автобуса. Она имеет равномерное распределение на отрезке [0,15]. Имеем

В рассматриваемом случае

Показательное распределение.

Показательным (экспоненциальным) распределением непрерывной случайной величины называется распределение, имеющее плотность вероятности вида:

где – постоянная положительная величина. Плотность вероятностей для показательного распределения для приведена ниже

Функция распределения вероятности для показательного распределения имеет вид:

Функция распределения для приведена ниже

Можно показать, что математическое ожидание и дисперсия случайной величины, имеющей экспоненциальное распределение, равны:

Пример. Установлено, что время горения электрической лампочки (Т) является случайной величиной, распределенной по показательному закону. Считая, что среднее значение этой величины равно 6 месяцам, найти вероятность того, что лампочка будет исправна более года.

Решение. Так как и функция распределения случайной величины T имеет вид

Поэтому

Лекция 9. Нормальное распределение и его свойства

Непрерывная случайная величина имеет нормальный закон распределения с параметрами и , если ее плотность вероятности имеет вид функции Гаусса

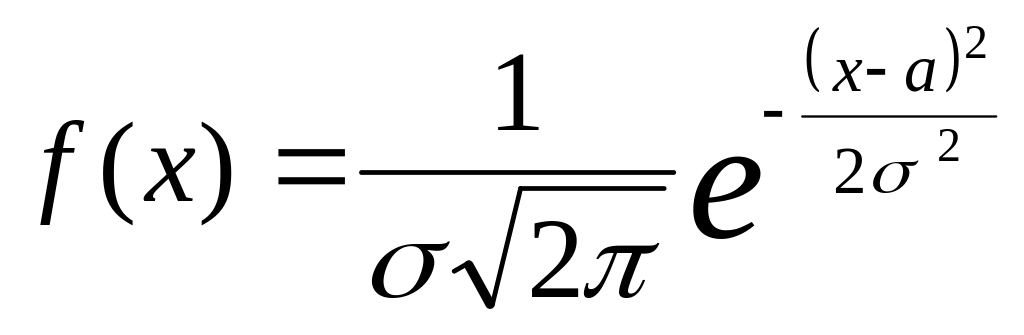
где . С помощью непосредственного вычисления математического ожидания и дисперсии нормального распределения легко выяснить вероятностный смысл его параметров: – есть математическое ожидание, а - среднее квадратическое отклонение нормального распределения. При распределение называется стандартным нормальным распределением.

Графики для ряда конкретных значений математического ожидания и среднего квадратического отклонения приведены ниже.

Рис. 1. Изменение вида функции при изменении математического ожидания

Рис. 2. Изменение при изменении среднего квадратического отклонения

Функция распределения в случае нормального распределения, очевидно, равна

.

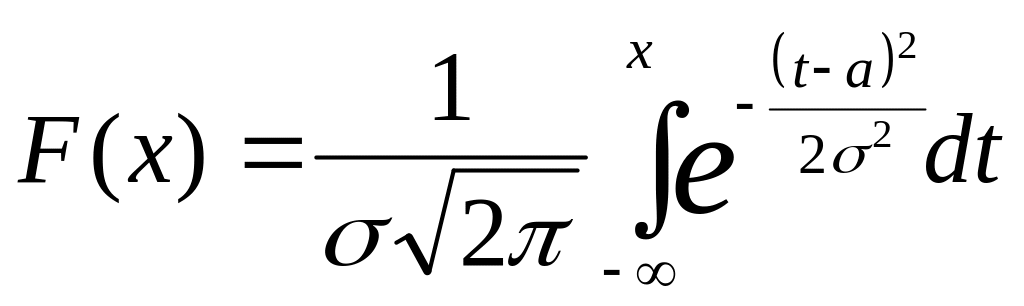Графики функции для ряда значений математического ожидания и среднего квадратического отклонения изображены на приводимых ниже рисунках

Рис. 3. Зависимость функции распределения от величины

Рис. 4. Зависимость функции распределения от величины

Нормальное распределение имеет исключительно важное значение для практических применений, так как многие непрерывные случайные величины описываются именно этим распределением. Оказывается, что суммирование большого числа случайных величин с различными законами распределения приводит к нормальному распределению результирующей суммы. Это свойство подтверждается центральной предельной теоремой (теорема Ляпунова). Смысл этой теоремы состоит в следующем. Если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.

Следует иметь в виду, что при усилении влияния отдельных факторов могут появляться отклонения от нормального распределения результирующего параметра. Поэтому большое значение на практике уделяется экспериментальной проверке выдвинутых гипотез, в том числе и гипотезы о нормальном распределении.