Лекция 8. Основные законы распределений случайных величин

Случайную величину полностью задает закон ее распределения (в дискретном случае), а также функция распределения или плотность вероятностей (для непрерывной случайной величины).

Наиболее важными законами распределения дискретной случайной величины являются биномиальный закон, закон распределения Пуассона, геометрическое и гипергеометрическое распределение, а непрерывной – нормальное, равномерное и показательное распределения. Нормальное распределение будет рассмотрено в одной из последующих лекций.

Биномиальное распределение, его математическое ожидание и дисперсия.

Закон распределения случайной величины числа появлений события в схеме Бернулли имеет вид

,

где , .

Эта формула еще называется биномиальной, так как её правая часть представляет собой -й член бинома Ньютона:

.

Очевидно, что для закона биномиального распределения вероятностей выполняется условие нормировки, т.е. сумма всех вероятностей равна единице:

.

Биномиальное распределение для и некоторых значений приведено ниже

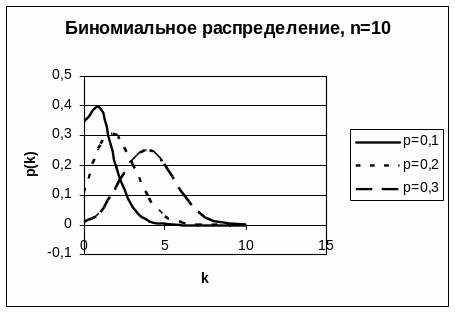
Математическое ожидание числа появлений события в независимых испытаниях для биномиального распределения равно произведению числа испытаний на вероятность появления события в каждом испытании (т.е. среднему числу появления события в данной серии испытаний).

Дисперсия и среднее квадратическое отклонения равны соответственно:

Распределение Пуассона.

Ранее отмечалось, что если при увеличении числа испытаний произведение остается постоянным, то биномиальное распределение при больших значениях n сходится к распределению Пуассона.

Случайная величина называется распределенной по закону Пуассона, если она может принимать значения , соответствующая вероятность которых определяется по формуле Пуассона:

,

Распределение Пуассона для приведено ниже

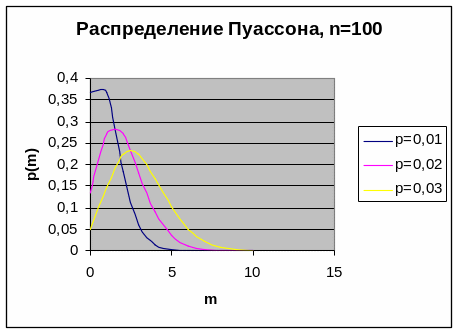
Для распределения Пуассона математическое ожидание и дисперсия равны соответственно:

.

Равенство значений математического ожидания и дисперсии является уникальным свойством распределения Пуассона. Это свойство часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина X распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики случайной величины – математическое ожидание и дисперсию. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении.

Геометрическое распределение

Дискретная случайная величина имеет геометрическое распределение, если она принимает значения (счетное множество значений) с вероятностями

.

Случайная величина, имеющая геометрическое распределение, представляет собой число испытаний в схеме Бернулли до первого успеха. Геометрическое распределение для некоторых конкретных значений p приведено ниже

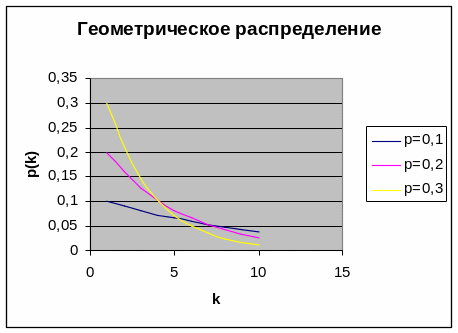
Можно показать, что математическое ожидание и дисперсия для геометрического распределения равны соответственно:

Пример. В большой партии изделий вероятность брака равна . Контроль качества проводится до первого появления бракованного изделия. В результате серии проверок обнаружилось, что бракованное изделие впервые появлялось в среднем при десятом испытании. Оценить численное значение .

Решение. Пусть - число испытаний до первого появления бракованного изделия. Эта случайная величина имеет геометрическое распределение. По условию ее среднее значение равно . Таким образом